2021 年“认证杯”网络挑战赛 B 题（第一阶段）

本人专挑数据挖掘、机器学习和 NLP 类型的题目做，有兴趣也可以逛逛我的数据挖掘竞赛专栏。

最后，本人不会回访，不互关，不互吹，以及谢绝诸如此类事

赛题官网：http://www.tzmcm.cn/

思路

该题若用数据分析的方法解决，可以看成一个聚类问题。但要对聚类有一个比较深的理解。比如，聚类时，量纲不同，可能导致聚类有偏向性。题目讲：毕星团的 Plx 大于在 $[20,22]$，因此，在聚类过程中，应该对 Plx 有所倾向。但如何控制这个倾向？

我认为：一是数据预处理；二是聚类算法和参数筛选上。

比如，在聚类之前，首先进行标准化，消除数据的量纲。之后，分析其他特征，如 B-V 等，与 Plx 是否存在关系？是否有影响，这些都需要通过数据的统计检验，或者是统计描述，如均值、方差等，看出来或检验出来。然后，再对 Plx 以及相关特征，乘以一个系数。

在聚类上，要考虑什么样的聚类结果是满意的？这个问题带有一定的主观性，可以结合其他论文，来考虑什么样的聚类是好的。然后再进行调参，一个一个试出来（本文用的是网格寻优法，类似于自动调参了）。若没有论文，可以考虑一些通用的、主观有利的准则，如：

1. 落在 $[20,22]$ 的个体，分布在多少个聚类簇上？设聚类簇数为 $x$
2. 落在 $[20,22]$ 的个体，落在哪个聚类簇上最多，最多是多少？，设最多为 $y$

若以 $x$ 优先，则倾向于严苛的筛选。若以 $y$ 优先，则放宽筛选。

聚类之后，我们把个体数最多的那个簇，作为毕星团即可。

但在此之前，必须先对数据做严密的分析。

数据预处理

数据分析

这部分其实没什么用，就是写给老师看看的。首先看看数据长啥样，数据一共 2719 条，9 个特征：

首先来看看统计描述（行星编号不计入）：

咱们可以看看 Plx 的 KDE（核密度图），如下所示：

可以看到的是，集中在 20-22 的样本居多。

我们看看 Plx 位于 $[20,22]$ 的数据：

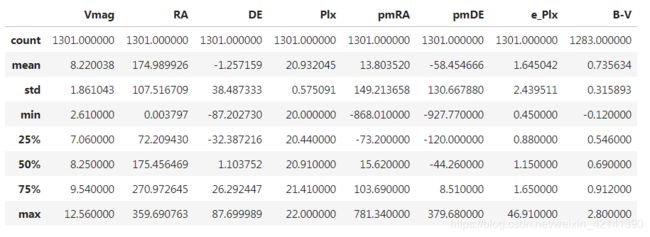
肉眼看到，除了 Vmag、RA、e_Plx、B-V 之外，其他列都有显著差异。不过为了验证这一点，我们还是对每一列进行 T 检验。比如对 Vmag，我们对全部数据，和 Plx 落在 $[20,22]$ 的数据进行两两 T 检验。

我们将原假设设置为：两个数据的均值相等，且很明显，根据 std，方差大体是不相等的。设置显著水平为 0.05，得出结论如下：

对于 Vmag 列，原假设不能被拒绝，所以大致认为：全部数据和[20,22]数据的Vmag列没有显著差异
对于 RA 列，原假设不能被拒绝，所以大致认为：全部数据和[20,22]数据的RA列没有显著差异
对于 DE 列，原假设不能被拒绝，所以大致认为：全部数据和[20,22]数据的DE列没有显著差异
对于 Plx 列，原假设被拒绝，所以有95%的把握认为：全部数据和[20,22]数据的Plx列有显著差异
对于 pmRA 列，原假设不能被拒绝，所以大致认为：全部数据和[20,22]数据的pmRA列没有显著差异
对于 pmDE 列，原假设不能被拒绝，所以大致认为：全部数据和[20,22]数据的pmDE列没有显著差异
对于 e_Plx 列，原假设不能被拒绝，所以大致认为：全部数据和[20,22]数据的e_Plx列没有显著差异
对于 B-V 列，原假设被拒绝，所以有95%的把握认为：全部数据和[20,22]数据的B-V列有显著差异

果然事实胜于雄辩，我们以为的 B-V 是有显著差异，但却原来却有显著性差异。不过无所谓，这只能表明，出了 Plx 和 B-V 外，全部数据和落在 $[20,22]$的数据的均值相同而已。

更一般的，我们可以来分析一下，全部数据和落在 $[20,22]$ 的数据是否具有相同的分布，为此，我们采用 Kruskal-Wallis H 检验。

原假设为：（对每一列）全部数据和落在 $[20,22]$ 的数据，具有相同分布。取显著水平为 0.05，结果如下：

对于 Vmag 列，原假设不能被拒绝，所以大致认为：全部数据和[20,22]数据的Vmag列分布相同
对于 RA 列，原假设不能被拒绝，所以大致认为：全部数据和[20,22]数据的RA列分布相同
对于 DE 列，原假设不能被拒绝，所以大致认为：全部数据和[20,22]数据的DE列分布相同
对于 Plx 列，原假设被拒绝，所以有95%的把握认为：全部数据和[20,22]数据的Plx列分布相同
对于 pmRA 列，原假设不能被拒绝，所以大致认为：全部数据和[20,22]数据的pmRA列分布相同
对于 pmDE 列，原假设不能被拒绝，所以大致认为：全部数据和[20,22]数据的pmDE列分布相同
对于 e_Plx 列，原假设不能被拒绝，所以大致认为：全部数据和[20,22]数据的e_Plx列分布相同
对于 B-V 列，原假设被拒绝，所以有95%的把握认为：全部数据和[20,22]数据的B-V列分布相同

好吧，我们不能拒绝这样一个事实，除了 Plx 和 B-V 列之外，全部数据和落在 $[20,22]$ 的数据，具有相同分布。而且根据 T 检验的结果，我们还不能拒绝他们有相同均值这一个事实。

机器学习模型→缺失数据

每一列的缺失数据如下：
{‘Vmag’: 0, ‘RA’: 0, ‘DE’: 0, ‘Plx’: 0, ‘pmRA’: 0, ‘pmDE’: 0, ‘e_Plx’: 0, ‘B-V’: 41}

其实第一阶段的题还是比较容易的，大家不要太担心。你看，只有 B-V 才有缺失值，而且结合上面的分析，Plx 和 B-V 的关系肯定不一般。

机器学习方法填充数据集

为了填充缺失数据，我们可以把其他列作为特征（除了编号外），B-V 作为待预测的 y 值。于是，考虑用一个机器学习模型，将那些 B-V 不是缺失值的数据作为数据集，训练出一个机器学习模型之后，再用模型的预测值，作为缺失值的填充值即可。

标准化

为了避免数据的量纲带来影响，在训练机器学习模型之前，必须消除量纲，为此这里采用均值-方差标准化，即将每一列数据的均值转换为 0，方差转换为 1 。

标准化后的数据如下所示：

统计描述如下：

筛选模型参数

鉴于数据量比较充足，我们就不用进行特征过滤了。不过，根据 没有免费午餐定则 ，我们首先要筛选机器学习算法。要筛选算法，必须先选模型参数。为此，我们从如下几个模型中筛选最优模型：

算法	线性回归	k近邻算法	支持向量机	决策树	随机森林	AdaBoost
符号	lr	kNN	SVR	dtr	rf	ada

其中随机森林的基模型是最大深度为 5 的决策树，AdaBoost 的基模型是线性回归。

为了筛选参数，首先需要构建一个参数网格，如下所示：

算法	参数网格
lr	无
kNN	{‘n_neighbors’:[3,5,7,9,11,13,15]}
SVR	grid = { ‘C’:[0.1, 0.25, 0.5, 0.75, 1, 1.25, 1.5, 1.75, 2, 2.25, 2.5, 2.75, 3], ‘kernel’:[‘linear’,‘rbf’,‘poly’], ‘epsilon’:[0, 0.01, 0.05, 0.1] }
dtr	grid = {‘max_depth’:[4, 9, 13, 17, 21, 25], ‘ccp_alpha’:[0,0.00025,0.0005,0.001,0.00125,0.0015,0.002,0.005,0.01,0.05,0.1]}
rf	基模型个数：5, 15, 25, 35, 45, 50, 65, 75, 85, 95
ada	基模型个数：5, 15, 25, 35, 45, 50, 65, 75, 85, 95

采用 5 折交叉验证、配合网格参数，以 MSE 为目标，最后筛选出模型如下：

筛选机器学习模型

在筛选完模型的最佳参数之后，将参数带入上述的机器学习算法之中，根据 5 折交叉验证，以 MSE 为目标，最后得出各算法在五折交叉验证中，每一次验证的 MSE 和均值，如下所示：

为了提高精确度，我们可以选择 线性回归、K近邻算法 或者 随机森林。

虽然看起来 rf 模型最好，但是我们还需要用 T 检验验证一下，我们个 lr 比较就好，设原假设为两组数据的均值相同，则通过 T 检验，于是可认为 lr 和 rf 模型等价。

进行 T 检验后，得出结论：

无法拒绝原假设，两个模型等价

于是，在效果相等的情况下，我们可以选择一个较为简单的模型，于是这里选择了 lr 模型。

模型训练和评价

将数据集拆分成训练集、测试集（7：3），在训练集上训练，在测试集上测试，最后得出 MSE 如下：

得到模型之后，我们就可以用 LR 模型，对 B-V 为 NAN 的那些数据进行预测，从而得出完整数据。

数据缺失部分如下所示（标准化后）：

神经网络模型→缺失值

由于 lr 模型的 MSE 实在太低，所以我们考虑用深度学习方法，搭建一个深度学习模型，最后用深度学习模型的预测值，去代替缺失值。

我们构造一个多层感知器，结构如下所示：

参数	取值	含义
units_list	[100, 200, 100, 50, 25, 10, 1]	隐藏层的层数和对应的神经元个数
‘optimizer’	adam	寻优算法
activation	relu	激活函数
init	init_uniform,	节点参数初始化方法
epochs	500	训练迭代次数
batch_size	200	batch 大小
rate	0.2	dropout 正则化率
loss	MAE	损失函数

同样按照 7:3 拆分数据集，以 MSE 为最后的训练结果如下：

考虑到最好的模型的 MSE 才 0.59，所以就不采用深度学习模型了。

（各位同学也注意，深度学习其实有时候不比机器学习好的，尤其是在 NLP 领域，这就是“天下没有午餐定则了”）

DBSCAN 聚类得出星群

在前面的分析中，我们知道 Plx 和 B-V 两个变量会比较敏感外，其他变量大多类似于一种“随机扰动”，所以，要用聚类的方法识别出毕星团，就不应该考虑“随机扰动”，或者更准确地，不能过分考虑“随机扰动”。

所以， 在标准化的基础上， 这里考虑给 Plx 和 B-V 乘以一个系数，以扩大聚类的影响。

聚类参数筛选——1

DBSCAN 聚类是一种聚类方法，但需要筛选两个参数：epsilon 和 min_samples，分别决定聚类时，动态聚类圈的直径大小，以及每一个聚类簇的最小样本量。

并且，我们也要筛选 Plx 和 B-V 的系数。要如何取得这些参数呢？我们可以参考机器学习填补缺失数据时的参数网格。但是，要如何判断聚类好，聚类坏，就要考我们主观断定了。

一个比较好的标准是：聚类应使得，那些 Plx 为[20, 22] 的点，落在尽可能同一个聚类簇上。因此，考核的标准就两个：

1. [20，22] 上的点一共落在多少个聚类簇上（至少两个）？
2. [20，22] 上的点，落在哪一个聚类簇上最多？一共多少个？

我们按照上述标准，以簇数为优先目标，以簇的最大聚类个体数为次要目标，筛选出最佳的聚类参数。簇数多意味着区分越严格，簇数少意味着不管其他特征如何，只要将 $[20，22]$ 集中在一个簇即可，要求较为宽松。

运用网格寻优法，定义参数网格如下：（在迭代过程中，若只有一个簇，则不考虑）

名称	参数
epsilon_list	1, 1.5, 2, 2.5, 3, 3.5
min_samples_list	2, 2.5, 3, 3.5, 4
coef_list	1.5, 2, 2.5, 3.0, 3.5, 4

结果如下：

聚类最佳参数为：
epsilon: 1：
min_samples: 2
系数： 4
簇最大个体数 603
簇数： 76

聚类参数筛选——2

另一个聚类参数筛选的办法是，以“拐点”作为筛选。

通过上述的分析，我得出：

$\cdots$
((1, 4, 3.5), (896, 46)),
((1, 4, 4), (896, 46)),
((1.5, 2, 1.5), (1225, 7)),
((1.5, 2, 2), (1225, 7)),
((1.5, 2, 2.5), (1225, 7)),
((1.5, 2, 3.0), (1225, 7)),
((1.5, 2, 3.5), (1225, 7)),

格式为：（epsilon, min_samples, 系数）, (簇最大个体数，簇数）

选拐点的一个好处：若根据方法一，则得出的筛选会比较严格。而将方法一的原则倒过来用，又会造成另一个极端。而是用拐点的方法恰到好处。

从上述分析可以看出，我们可以选择参数：epsilon=1, min_samples=4, 系数=4。

不过，本文考虑再三，还是采用方法 1。毕竟，1225 个参数，已经几乎等于落在 $[20,22]$ 的个体数了，所以已经是到达极端了，故不考虑用。

结果与 H-R 图

毕星团 HIP：

得出聚类结果后，选择个体数最多的那个簇，旗下的所有个体，且 Plx 落在 $[20,22]$ 的便是毕星团的一份子了。结果如下：

135 223 305 475 606 924 943 1134 1144 1402
1427 157
$\cdots$
109624 109655 110084 110776 111143 111407 113148 113495 113782 114131
115430 116352 117461

绘制 H-R 图

根据 H-R 图的定义：

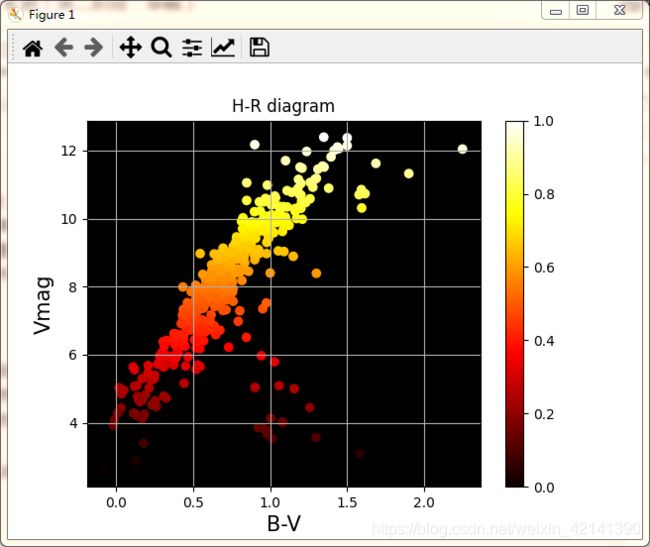
原始的图在水平轴上显示恒星的光谱类型，在垂直的轴上显示绝对视星等。光谱类型不是数值的量，但其序列反映出恒星表面温度的单调序列。现代观测版本的图表将光谱类型替换成色指数（在20世纪的图表中，最常见的是恒星的B-V色指数）。这种类型的图表通常称为观测赫罗图，或特殊的色光图（CMD，color–magnitude diagram），并且通常是观测者在使用。在已知恒星处于相同距离（如恒星簇内）的情况下，CMD通常用于描述星团中的恒星，其垂直轴视恒星的视星等 ¹

根据上述描述，我们以 B-V 为 x 轴，以 视星为 y 轴，绘制 H-R 图如下（其中点的颜色与 B-V 有关）：

代码与提问

若需要代码，请关注、私信、说明题目和年份

如果有其他问题，请到评论区留言，私信提问，概不回答。也在此鼓励大家独立思考。

本人不会回访，不互关，不互吹，以及谢绝诸如此类事

如果本篇博文对您有所帮助，请不要吝啬您的点赞

第二阶段：https://blog.csdn.net/weixin_42141390/article/details/116830451

如果有其他编程问题和原理问题，请再评论区留言，私信一概不回。也鼓励大家独立思考。

---

1. 摘抄自维基百科 ↩︎