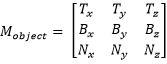法线贴图是一副纹理图,只是纹理图上的点保存的不是RGB数据,我们是将压缩过的x,y,z轴坐标保存到red,greed,blue分量中,这个xyz坐标定义了一个法线方向
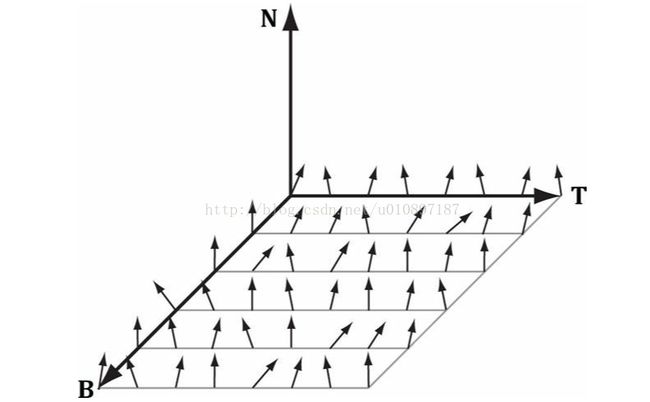
因此法线贴图的每个像素都保存了一个法线向量。下图显示了一个形象的normal map例子:
保存在法线贴图中的法线是相对于由向量T(x轴),B(y轴),N(z轴)定义的纹理空间坐标系的
T向量在纹理图像中是水平向右的,B向量在纹理图像中是竖直向下的,N向量是和纹理平面正交的
Note:正如上图中显示的,这些向量通常是z轴对齐的(上图中N是z轴),因此z轴坐标占有最大的量,
所以,当将法线贴图作为颜色图像来浏览时,通常显示为蓝色。这是因为z轴坐标是保存在蓝色通道而且有最大的量,颜色上占有主导地位
那么我们该怎么将一个单位向量压缩为这种格式呢?首先注意的是对于一个单位向量而言,每个分量坐标总是位于[-1,1]的范围内
假如我们将这个范围偏移并缩放为[0,1]并且乘以255并截断为十进制,那么结果将会变为[0,255]范围内的一个整数,就是说,
假如x是一个在[-1,1]范围内的坐标值,那么整数部分f(x)是一个在范围0-255内的整数,函数定义为:
因此保存一个单位向量在一个24位图像中,我们仅对每个坐标应用函数f(x),并且将得到的值写到纹理图的相应颜色通道中
下一个问题是如何恢复压缩操作,也就是说,给定一个范围在0-255的压缩过的纹理坐标,怎样才能恢复在[-1,1]范围内的真值
方法是简单的应用函数f(x)的逆,稍微思考一下,我们能得到这个公式:
那就是说,假如x是一个属于0-255范围内的整数,那么
是一个在[-1,1]范围内的浮点数
我们不需要自己做压缩操作,我们可以使用PhotoShop插件将图像转换为法线贴图,
然而,当我们在像素着色器中对法线贴图进行采样时,我们将不得不做恢复操作的部分以将其解压缩。
当我们在着色器中像下面这样采样法线贴图:
float3 normalT = gNormalMap.Sample(gTriLinearSam , pin.Tex);
颜色向量normalT将得到规格化的分量(r,g,b), 0 ≤r, g, b≤ 1
因此这个方法已经为我们做了一部分解压操作(即除以255,用于将一个0-255范围内的数转换到浮点数区间[0 ,1])
我们通过偏移,缩放将每个分量从[0 , 1]转换到[-1 , 1]完成操作,使用函数g: [0 , 1]→[-1 , 1] , 定义如下:
在代码中,我们像这样对每个颜色分量应用这个函数:
//Uncompress each component from [0 , 1] to [-1 , 1]
normalT = 2.0f * normalT - 1.0f;
这个标量1.0被解释为向量(1 , 1 , 1),使得表达式有意义并且可以逐分量运算
考虑一个3D纹理映射三角形,为了便于讨论,假设纹理映射没有失真,换句话说,映射纹理三角形到3D三角形需要进行一个
刚体变换(平移和缩放),现在,假设纹理像一幅贴花纸,因为我要拿起贴花纸,然后移动它,旋转它,使其与3D三角形重合。
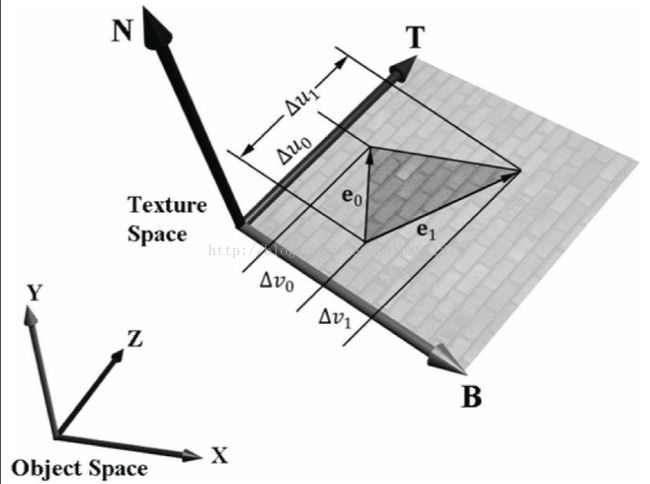
图2显示了3D三角形的纹理空间坐标系:它们与三角形相切,且位于三角形平面。当然,三角形的纹理坐标时相对于纹理空间坐标系。
结合三角形面法线N,我们在三角形平面获得一个基于TBN的三维坐标系,我们将其叫做纹理空间或者切线空间。
注意切线空间通常是从一个三角形变换到另一个三角形(见图三)
图2:三角形的纹理空间和对象空间的关系。3D切线向量T与纹理坐标系的u轴对应,3D切线向量B与纹理坐标系的v轴对应
图3:盒子的每个面的纹理空间是不同的
正如图1所示,在法线贴图中的法线向量是定义在纹理空间(即切线空间)的, 但是我们的光线是定义在世界坐标系空间。
为了进行光照计算,法线向量和光线需要在同一空间。因此我们要做的第一步是找到切线空间坐标系与对象空间坐标系(物体的局部坐标系)
的关联。一旦我们是在对象空间(局部坐标系),我们能够使用世界矩阵将其从局部空间转换到世界空间。用v0 , v1 , v2表示对应的纹理坐标为
(u0 , v0) , (u1 , v1) , (u2 , v2) 的三个顶点,这三个顶点定义了一个相对于纹理空间轴(如,T和B)的纹理平面。让
,
作为3D三角形的两条边向量,其对应的纹理坐标为
和
看图2,能够清楚的得出:
用相对于局部空间的坐标表示向量,我们能得到以下这个矩阵等式:
注意:我们知道三角形顶点的局部空间坐标,因此我们知道边向量的局部空间坐标,因此矩阵:
是已知的,同样的,我们也知道顶点的纹理坐标,因此矩阵:
也是已知的,为了解出T,B的局部空间坐标,我们得到以下的式子:
在上面,我们使用了定理,矩阵
的逆为:
注意:向量T,B在局部空间中通常不是单位长度,假如纹理失真,他们将不再正交
向量T,B和N通常分别被简称为切线,副法线(副切线),和法线向量
我们已经推导了每个三角形的切线空间,然而,假如我们为法线贴图使用这个纹理空间(切线空间),我们将得到一个三角形的外观
因为这个三角形的切线空间是恒定的。因此,我们为每个顶点指定其切线空间,我们做了与顶点法线逼近平滑曲面同样的取平均值技巧:
1:面元的任意顶点的切线向量T由面元中所有共享该顶点的三角形的切线向量取平均值得到
2:面元的任意顶点的副切线向量B由面元中所有共享该顶点的三角形的副切线向量取平均值计算得到
通常来说,取均值后,基于TBN的坐标系将会正交,因此TBN向量是相互正交的且为单位长度。
这通常由施密特程序来完成。为任意三角形面元的每一个顶点生成切线坐标的代码在网页:点击打开链接中是可用的
在我们的系统中,我们将不直接将副法线向量B保存在内存中,相应的,当我们需要B向量时,我们可以计算B = N x T
N是平均顶点法线,因此,我们的顶点结构体应该是这样的:
namespaceVertex
{
structNormalMap {
XMFLOAT3 Pos;
XMFLOAT3 Normal;
XMFLOAT2 Tex;
XMFLOAT3 TangentU;
};
}
在程序中,由GeometryGenerator创建生成的面元计算纹理空间(切线空间)中与u轴对于的切线向量T。
正方体和网格中每个顶点的切线向量T的局部空间坐标都是非常容易指定的,对于圆柱和球体,每个顶点的切线向量T
可以通过由两个变量组成的矢量值函数计算偏导数
得到
参数u是纹理坐标u
此时,我们能够得到面元中每个顶点的TBN正交坐标系(切线坐标系)。而且,我们有TBN向量在面元局部空间中的坐标。
现在我们有基于TBN向量为坐标轴(切线空间)的点的坐标,我们能够将坐标从切线空间转换到局部空间,使用这个矩阵: