决策和影响同时发生。
在做决策时必须设想如果自己处于其他参与者的位置,会怎样做决策?这个决策会给自己带来什么影响
决策树适用于一个人面临各种选择时的描述分析,而博弈树则适用于多个参与者在一场策略博弈中的决策次序的描述分析。
谈判的一个特征在于时间就是金钱,谈判的时间拉得越长,蛋糕就会缩水,各方的利益也会受损。
只有一步的情况
此时阿里处于一个非常强势的地位,他的提议可以使巴巴有所收获或者一无所获。即使阿里提出独享整个蛋糕,巴巴也只能无奈地接受。
两轮谈判的情况
巴巴占优势,阿里会阻止第二轮谈判的发生,所以他会在一开始就提出与巴巴平分蛋糕,这刚好足够引诱对方接受,也能为自己保证一半的收益。
三轮谈判的情况
阿里知道会有这个结果,所以从一开始,他就会许诺分给巴巴1/3的蛋糕(刚好足够引诱对方接受),而自己得到2/3的蛋糕。
假如谈判的轮数是偶数,则阿里应在一开始就提出和巴巴各得一半蛋糕;假如谈判的轮数是奇数,阿里应该提议分给巴巴(n-1)/2n,自己得(n+1)/2n。
注意
1妥协的解决方案是很难避免的。当然最后一个提出条件的人可以得到剩下的全部成果,但如果真的走到这一步,大概成 果也所剩无几了。
2谈判的开始就提出一个刚好足够引诱对方接受的条件。
3在谈判开始之前就已经确定了最后结果。因此策略行动的时间可能会提前,在确定谈判规则的时候就已经开始了。
4想要成功应用向前展望,倒后推理法则,我们需要明确两个前提:首先,后行动者可以观察到先行动者的动作。其次,策略是不可以逆转的。
博弈是同时进行的,他们都需要在不知道对方行动方案的情况下做出选择。
比如杂志同时决定上市策略
基于两个简单的概念:优势策略和均衡。
优势策略
优势策略“的“优势“是指你的这个策略(A1)比其他策略(A2、A3)占有优势,而不是比你对手的策略(B1、B2、B3)更有优势。无论对方如何行动,采取优势策略带来的结果一定比采取任何其他策略带来的结果好。
法则1:假如你有一个优势策略,请照办。
法则2:剔除所有的劣势策略,不予考虑,如此一步一步做下去。
各方的行动就是针对对方行动确定的最佳策略。一旦知道对手在做什么,没人会更改自己的做法。博弈论学者把这个结果称为”均衡”,
法则3:寻找这个博弈的均衡,即一对策略,按照这对策略行事,各个参与者的行动都是对对方行动的最佳回应。
惩罚原则
要想杜绝作弊行为就必须对作弊者进行惩罚。除了一次性的惩罚,还存在另一种惩罚:当博弈反复进行时,这一回合的作弊所得将导致其他回合的损失。
以牙还牙
区别对待的策略
指导原则:
开始合作;
继续合作;
计算在你合作的情况下对方看上去背叛了多少次;
假如这一百分比变得令人难以接受,就开始使用以牙还牙策略。
事例
第一印象:绝对不能接受第一轮就背叛。转向以牙还牙策略。
短期:任何3轮当中出现2次背叛也是不能接受的,转向以牙还牙策略。
中期:过去20轮当中出现3次背叛也是不能接受的,转向以牙还牙策略。
长期:过去100轮当中出现5次背叛也是不能接受的,转向以牙还牙策略。
焦土政策
斯大林的焦土政策是策略行动的一个例子。一个策略行动,其设计意图在于改变对方的看法和行动,使之变得对自己有利,最突出的特征是刻意限制自己的行动自由。
因为你的做法改变了其他参与者对你的行动预期,你可以充分利用这一点,为自己谋利。其他人知道,只要你有行动的自由,你就有让步的自由。
因为你的做法改变了其他参与者对你的行动预期,你可以充分利用这一点,为自己谋利。其他人知道,只要你有行动的自由,你就有让步的自由。
分析
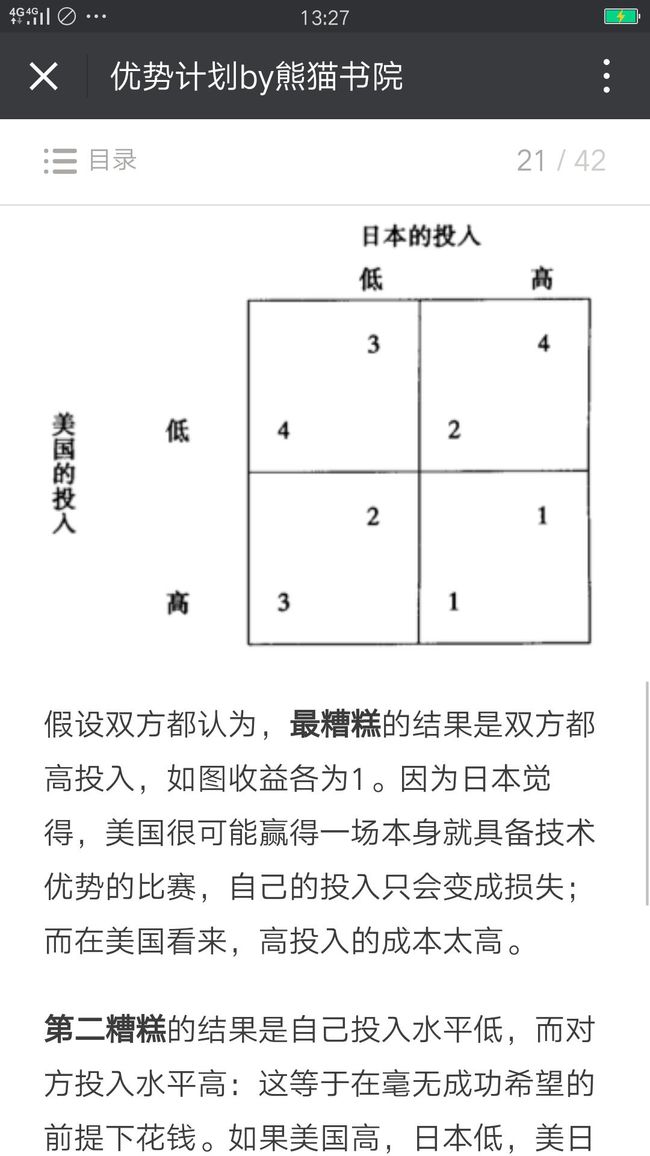
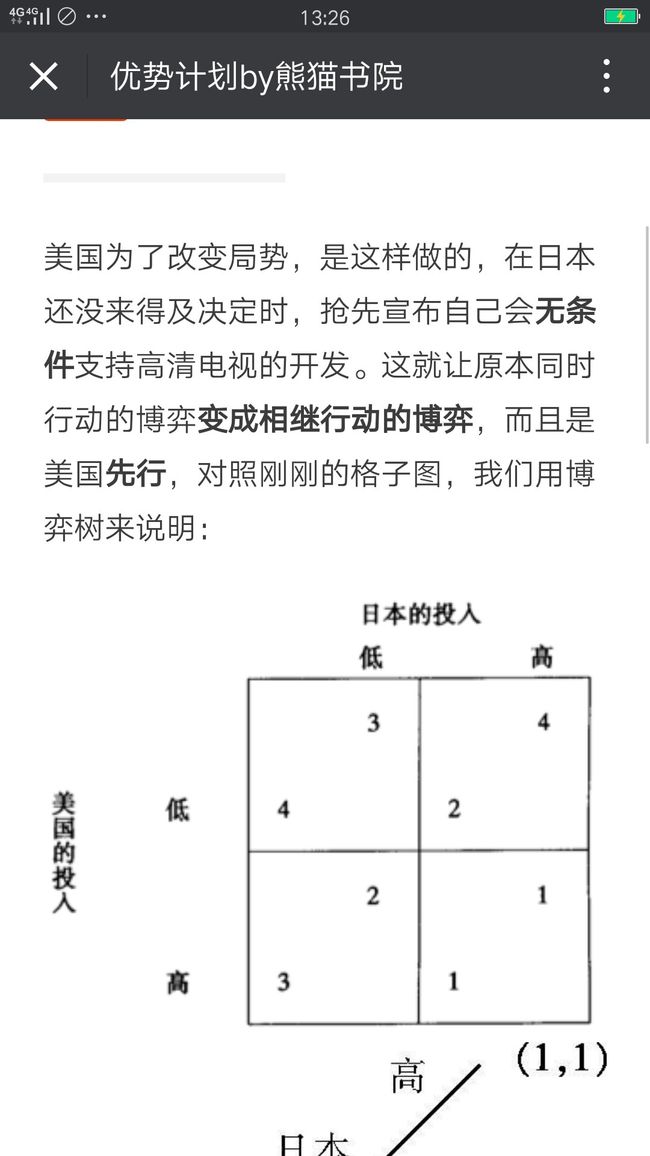
这个策略行动的巧妙之处,在于美国单方面、无条件地宣布了自己的选择,于是展开了有利的形势。这个选择不是美国在同时行动的博弈里会做出的选择。美国如果宣布选择低投入,得不到任何好处,因为美国不做声明,日本也会这么预期。要想策略地行动,就不能采取在同时行动博弈里的均衡策略。美国这一出人意料的行动改变了日本的预期,进而改变了日本的选择。
一旦预期美国选择高投入,日本就会选择低投入。当然等日本拿定了主意,美国最好还是改变主意,回到低水平的选择上,这样可以为自己获得4的结果。
换句话说,美国无条件行动的第一步的可信度是关键。假如美国并不可信,那么这一招不会有用。为了让一个策略行动变得可信,就得采取其他的附加行动,让改变选择变得代价高昂甚至完全没有可能。所以,要对这个策略行动做出一个承诺。
总结
一个策略行动包含了两点:计划好的行动路线以及使这一路线显得可信的承诺。
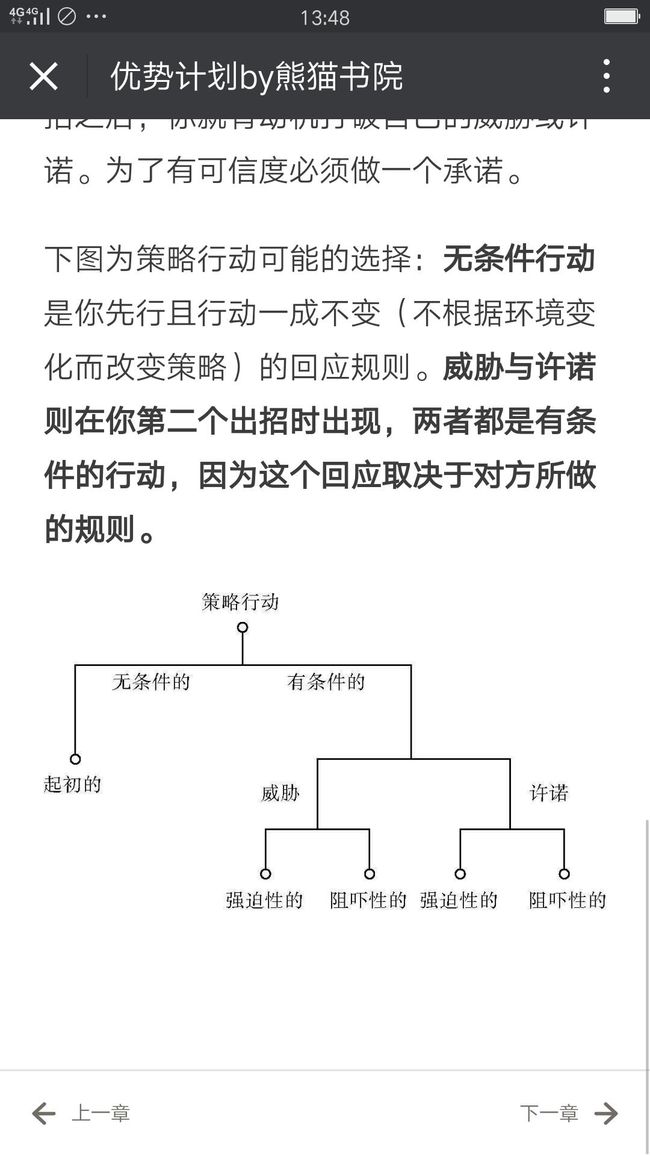
假如你没有先行,仍然可以通过对一个回应规则做出承诺,然后获得相仿的策略优势。这是有条件的策略行动。
回应规则分为两大类:威胁与许诺。
威胁是对不愿与你合作的人实施惩罚的一种回应规则。
一种是强迫性的威胁,例如恐怖分子劫持飞机,他的回应规则是:假如他的要求不能被满足,就会炸毁飞机;另一种是阻吓性的威胁,比如美国威胁说,如果苏联出兵攻击任何一个北约国家,它就会动用核武器回击。强迫性的威胁意在促使某人采取行动,而阻吓性的威胁意在阻止某人采取行动。两种威胁都会有同样的结局:如果不得不实施威胁,双方都要大吃苦头。
许诺是向愿与你合作的人提供回报的方式。
许诺也分为强迫性的和阻吓性的两种。强迫性许诺意在促使某人采取对你有利的行动;阻吓性许诺意在阻止某人采取对你不利的行动 。
所有的威胁与许诺都有一定的回应规则,你不会在没有回应规则的前提下行动。不过有时候,说明什么事情会在没有回应规则的情况下发生,仍然有公告天下的作用,这就是警告和保证。
如果实践一个“威胁”对你有利,就是警告
如果实践一个“许诺”对你有利,就是保证。
威胁与许诺是真正的策略行动,而警告与保证是起一个告知作用,
你不一定直接建立一个回应规则,相反,你可以故意让别人利用这些策略当中的一个,例如:
你可以任由别人在你回应前采取一个无条件行动。无条件行动是你先行且行动一成不变(不根据环境变化而改变策略)的回应规则。
你可以等别人发出一个威胁,然后再行动。
你可以等别人提出一个许诺,然后再行动。
原本可以率先行动的一方放弃这一便利,让对方做出一个无条件的行动,反而可能取得更好的结果。但这不是一个基本规则。有时你可能是想阻止你的对手做出一个无条件的承诺。孙子曾说过:“围师遗阙”,意思是包围敌人,要留出口。只要留下出口,敌人就会认定还有机会逃走;而一旦敌人看不到任何逃跑的机会,就会被激发出破釜沉舟的勇气。
在你许诺时不应让许诺超过必要的范围。如果许诺确实影响了对方的行为,你就要准备践行诺言。这件事做起来应该是代价越小越好,所以许诺只要达到必要的最低限度就行了。同样的,你不应让你的威胁超过必要的范围,
现实与理想有一定的差别,威胁时要选择大小和可信度。
结论
能奏效的最小而又最恰当的威胁应该成为威胁发出者的首选,一定要让惩罚与罪行相适应
比如
如果美国想日本多买柑橘和牛肉,应该选一个互惠性质的威胁。比如,美国可以威胁削减日本电器和汽车的进口配额。而不是选择动用武力
你如果想临时变化规则 你必须让别人相信你确实会实践你的无条件行动、威胁和许诺 ,你的承诺可能会受到检验,你必须努力争取可信度
有八种帮助建立可信度的方法,被称为“八正道”。这八正道是建立在三个重要原则上的。
第一个原则:改变博弈的结果。也就是说,务必让遵守你的承诺成为符合你自身利益的选择:把威胁变成警告,把许诺变成保证。对应的“正道”有:
1.建立和利用一种信誉。
2.写下合同。
第二个原则:改变博弈,让你背弃承诺的能力大受限制。对应的”正道”是:
3.切断沟通。
4.破釜沉舟。
5.让后果超出你的控制。
违背其中一个小承诺的收益很可能不足以抵消失去余下承诺的损失。因此第六个”正道”是:
6.小步前进
第三个原则:充分利用别人的力量帮助自己遵守承诺。对应的”正道”是:
7.通过团队合作建立可信度。
8.雇用谈判代理人。
举例
一是通过建立信誉带来可信度。例如第三次柏林危机。
二是通过破坏信誉为达成一个承诺铺设道路。
比如
为了保证合同的落实,需要某个具有独立动机的个人或机构来负责强迫执行承诺或者收取罚金。
(四)破釜沉舟
军队常常用断绝自己后路的做法来达成遵守承诺的目标
所以,破釜沉舟的策略需要指挥者让自己的士兵们透彻了解,否则就只是作战室里的异想天开
“奇爱博士
边缘政策是故意创造一种可以辨认的风险,一种人们不能完全控制的风险。
小步前进
如果把承诺的问题缩小到一个足够小的范围,就能解决可信度的问题。你可以将威胁或许诺分解为许多小问题,让每一个问题都可以单独解决。
如果大承诺不可行,你可以选一个小的承诺,重复使用。比如装修分每周付款
团队合作
这个会员超过200万的组织里,成员之间通过互相分享经历、希望和力量,来达到戒酒的目的,帮助自己,也帮助他人。谁如果反悔食言,荣誉和自尊就会付诸东流。
八雇佣谈判代理人
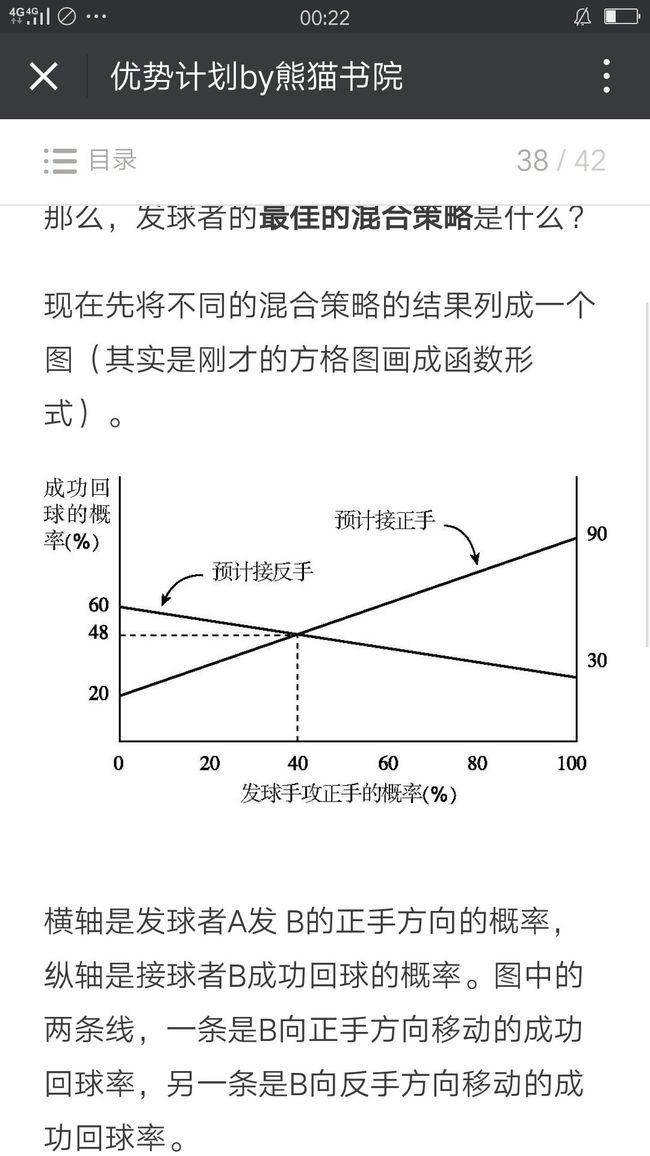
打网球的例子
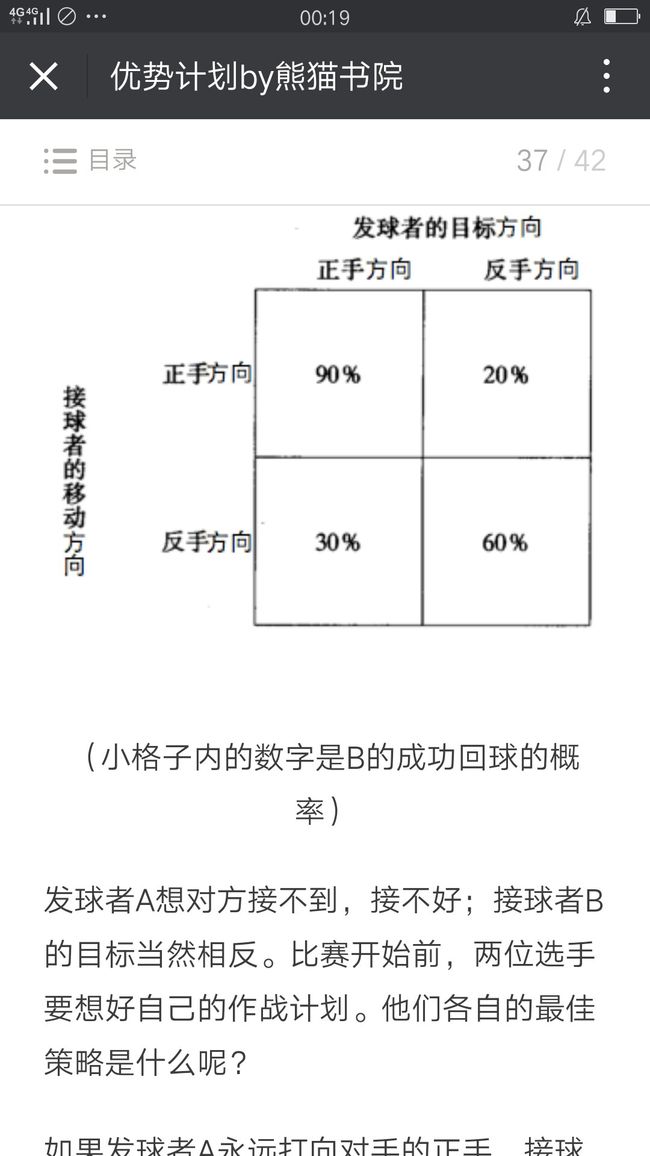
这两条线的交点——40%,非常关键,当A发正手方向球的概率为40%时(40:60的混合策略),B没法从A的混合策略中占到任何便宜。
不同的选手有不同的绝对优势和相对优势,所以上述矩阵里的90%,60%,30%,和20%的概率也会有相应的变化,最佳的混合策略也会不同。
对于发球者A,如果发对方B的正手方向的球,就要观察对方选择两种不同的回应方式会有什么不同的结果。还是上面的图和例子,当A发正手方向,B对应的差值是90%-30%=60%。当A发反手方向,对应的差值是60%-20%=40%。
将这两个数字倒过来,就能得到最佳混合策略的比例。
同样的,对于接球者B来说,当他选择正手方向去接球,A对应的差为:90%-20%=70%。当B选择反手方向去接球,对应的差60%-30%=30%。把这两个数字倒过来,就得到了最佳混合策略比例。所以,接球者B应该按30:70的比例接正手方向和反手方向的球。
接球者B采用自己的最佳混合策略时,发球者A的成功率是48%。发球者A采用自己的最佳混合策略时,接球者的成功率是48%。这不是巧合,而是双方利益严格对立的所有博弈中的共同点。
最小最大定理
在零和博弈里,参与者的利益严格相反(一人所得等于另一人所失),每个参与者尽量使对手的最大收益最小化,而他的对手则努力使自己的最小收益最大化。这样的行动策略会导致一个令人惊讶的结果:最大收益的最小值(最小最大收益)等于最小收益的最大值(最大最小收益)。双方都无法再改善自己的地位,此时形成了这个博弈的均衡。
适用范围
刚刚讲过的图表和分析方法能解决所有只有两个参与者且他们各有两个策略的零和博弈。但这些方法并不适合非零和博弈,也不适用于参与者数目超过两个,或者他们拥有的策略数目超过两个的零和博弈。
运用方法
(一)坚持正确的混合比率
例如,在刚刚说的网球的例子中,当发球者A采用自己的最佳混合策略,按照40∶60的比例发对方正手方向和反手方向的球时,接球者B的成功率为48%。而如果A用其他任何比例,接球者的成功率都会上升。
(二)坚持随机性
但是,这种有规则的行为很快就会被接球者B识破,B随即做出正确的策略,因此成功率上升为(4/10)×90%+(6/10)×60%=72%。如果发球者A想取得最好效果,在保证总体混合比例的同时,必须使每一次发球的方向都不可预测。
(三)如何在固定混合比率下随机行动?
举个例子,手表上的秒针可以帮助我们获得任何混合策略比例,发球者A的最佳混合策略是40:60,A可以选择在秒针落在1~24之间时发B正手方向的球,秒针落在25~60之间时发B反手方向的球