leetcode 518. 零钱兑换 II-----完全背包套路模板
零钱兑换 II 题解集合
- 完全背包(朴素解法)
- 完全背包(一维优化)
- 注意双重for循环的顺序
- 动态规划注意事项总结
- 记忆化搜索解法
完全背包(朴素解法)
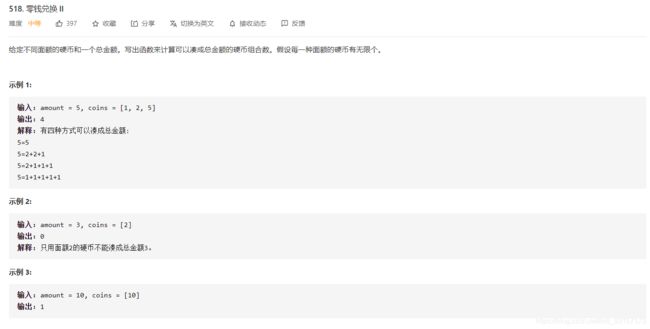
- 在leetcode 322. 零钱兑换中,我们求的是「取得特定价值所需要的最小物品个数」。
- 对于本题,我们求的是「取得特定价值的方案数量」。
- 求的东西不一样,但问题的本质没有发生改变,同样属于「组合优化」问题。
- 你可以这样来理解什么是「组合问题」:
- 被选物品之间不需要满足特定关系,只需要选择物品,以达到「全局最优」或者「特定状态」即可。
- 同时硬币相当于我们的物品,每种硬币可以选择「无限次」,很自然的想到「完全背包」。
- 这时候可以将「完全背包」的状态定义搬过来进行“微调”:
- 定义 dp[i][j] 为考虑前 i 件物品,凑成总和为 j 的方案数量。
- 为了方便初始化,我们一般让 dp[0][x] 代表不考虑任何物品的情况。
- 因此我们有显而易见的初始化条件:dp[0][0]=1,其余dp[0][x]=0 。
- 代表当没有任何硬币的时候,存在凑成总和为 0 的方案数量为 1;凑成其他总和的方案不存在。
- 当「状态定义」与「基本初始化」有了之后,我们不失一般性的考虑 dp[i][j] 该如何转移。
- 对于第 i 个硬币我们有两种决策方案:
不使用该硬币:
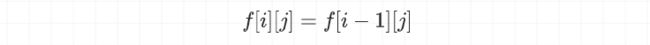
使用该硬币:由于每个硬币可以被选择多次(容量允许的情况下),因此方案数量应当是选择「任意个」该硬币的方案总和:
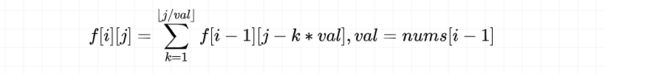
图解:

代码:
class Solution {
public:
int change(int amount, vector<int>& coins)
{
int size = coins.size();//物品的个数
vector<vector<int>> dp(size + 1, vector<int>(amount + 1, 0));
//考虑什么物品都不选的初始情况
dp[0][0] = 1;//当什么物品都不考虑,并且背包容量为0的时候,为一种符合条件
//考虑其他物品的情况
for (int i = 1; i <=size; i++)
{
int val = coins[i-1];//获取当前物品的大小
for (int j = 0; j <= amount; j++)
{
//不选当前硬币
dp[i][j] = dp[i - 1][j];
//选当前硬币--注意最后总方案是选当前硬币和不选当前硬币可行方案数之和
for (int k = 1; k * val <= j; k++)
dp[i][j] += dp[i - 1][j - k * val];
}
}
return dp[size][amount];
}
};
完全背包(一维优化)
- 显然二维完全背包求解方案复杂度有点高。
- 我们需要对其进行「降维优化」,可以使用 数学分析方式,或者 换元优化方式 进行降维优化。
- 由于 数学分析方式 十分耗时,我们用得更多的 换元优化方式。两者同样具有「可推广」特性。
- 因为后者更为常用,所以我们再来回顾一下如何进行 换元一维优化 :
在二维解法的基础上,直接取消「物品维度」确保「容量维度」的遍历顺序为「从小到大」(适用于「完全背包」)将形如 dp[i][j-k*val] 的式子更替为 dp[j-val],同时解决「数组越界」问题(将物品维度的遍历修改为从 val 开始)
代码:
class Solution {
public:
int change(int amount, vector<int>& coins)
{
int size = coins.size();//物品的个数
vector<int> dp(amount + 1);
//考虑什么物品都不选的初始情况
dp[0] = 1;//当什么物品都不考虑,并且背包容量为0的时候,为一种符合条件
//考虑其他物品的情况
for (int i = 1; i <=size; i++)
{
int val = coins[i-1];//获取当前物品的大小
//同时解决「数组越界」问题(将物品维度的遍历修改为从 val 开始)
for (int j = val; j <= amount; j++)
{
dp[j] += dp[j - val];
}
}
return dp[amount];
}
};
注意双重for循环的顺序
之前我在完全背包这篇文章结尾提到过排列数和组合数的概念,但什么时候会遇到,没有说,今天它来了
本题和纯完全背包不一样,纯完全背包是能否凑成总金额,而本题是要求凑成总金额的个数!
注意题目描述中是凑成总金额的硬币组合数,为什么强调是组合数呢?
例如示例一:
5 = 2 + 2 + 1
5 = 2 + 1 + 2
这是一种组合,都是 2 2 1。
如果问的是排列数,那么上面就是两种排列了。
组合不强调元素之间的顺序,排列强调元素之间的顺序。
下面再啰嗦一下动态规划五部曲,上面没有说:
1.确定dp数组以及下标的含义
dp[j]:凑成总金额j的货币组合数为dp[j]
2.确定递推公式
dp[j] (考虑coins[i]的组合总和) 就是所有的dp[j - coins[i]](不考虑coins[i])相加。
所以递推公式:dp[j] += dp[j - coins[i]];
求装满背包有几种方法,一般公式都是:dp[j] += dp[j - nums[i]];
3.dp数组如何初始化
首先dp[0]一定要为1,dp[0] = 1是 递归公式的基础。
从dp[i]的含义上来讲就是,凑成总金额0的货币组合数为1。
下标非0的dp[j]初始化为0,这样累计加dp[j - coins[i]]的时候才不会影响真正的dp[j]
4.确定遍历顺序
本题中我们是外层for循环遍历物品(钱币),内层for遍历背包(金钱总额),还是外层for遍历背包(金钱总额),内层for循环遍历物品(钱币)呢?
完全背包的两个for循环的先后顺序都是可以的。
但本题就不行了!
因为纯完全背包求得是能否凑成总和,和凑成总和的元素有没有顺序没关系,即:有顺序也行,没有顺序也行!
而本题要求凑成总和的组合数,元素之间要求没有顺序。
所以纯完全背包是能凑成总结就行,不用管怎么凑的。
本题是求凑出来的方案个数,且每个方案个数是为组合数。
那么本题,两个for循环的先后顺序可就有说法了。
我们先来看 外层for循环遍历物品(钱币),内层for遍历背包(金钱总额)的情况。
代码如下:
for (int i = 0; i < coins.size(); i++) {
// 遍历物品
for (int j = coins[i]; j <= amount; j++) {
// 遍历背包容量
dp[j] += dp[j - coins[i]];
}
}
假设:coins[0] = 1,coins[1] = 5。
那么就是先把1加入计算,然后再把5加入计算,得到的方法数量只有{1, 5}这种情况。而不会出现{5, 1}的情况。
所以这种遍历顺序中dp[j]里计算的是组合数!
如果把两个for交换顺序,代码如下:
for (int j = 0; j <= amount; j++) {
// 遍历背包容量
for (int i = 0; i < coins.size(); i++) {
// 遍历物品
if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];
}
}
背包容量的每一个值,都是经过 1 和 5 的计算,包含了{1, 5} 和 {5, 1}两种情况。
此时dp[j]里算出来的就是排列数!
5.举例推导dp数组
输入: amount = 5, coins = [1, 2, 5] ,dp状态图如下:
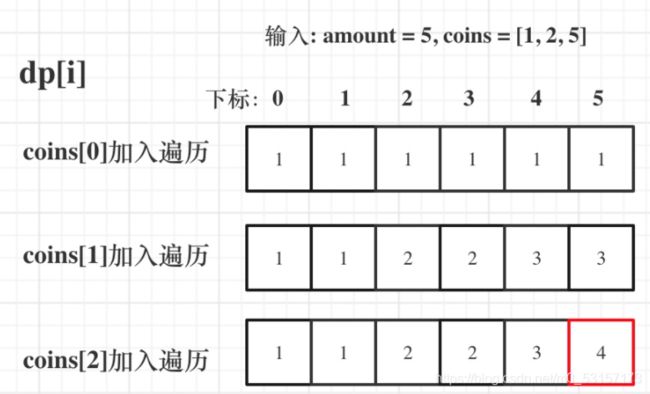
最后红色框dp[amount]为最终结果。
以上分析完毕,C++代码如下:
class Solution {
public:
int change(int amount, vector<int>& coins) {
vector<int> dp(amount + 1, 0);
dp[0] = 1;
for (int i = 0; i < coins.size(); i++) {
// 遍历物品
for (int j = coins[i]; j <= amount; j++) {
// 遍历背包
dp[j] += dp[j - coins[i]];
}
}
return dp[amount];
}
};
动态规划注意事项总结
在求装满背包有几种方案的时候,认清遍历顺序是非常关键的。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
记忆化搜索解法
- 递归的结束条件:凑出了目标钱数,找到了一种方案,返回1 , 或者枚举完了所有硬币,即越界了,说明当前没有可行方案,返回0
- 递归返回值:返回当前方案数
- 本级递归做什么:遍历硬币数组,对于当前硬币选择若干张,使得剩余目标钱等于0。可能存在的方案数进行累加求和
注意暴力递归会超时,这里还需要用依赖哈希表来存储已经求出来的结果,防止重复计算
其实如果用递归解,最好的方法还是把问题转化为多叉树的遍历,比较容易理解
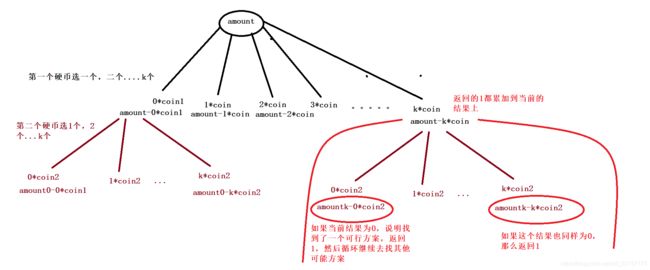
那么重复计算是从哪里来的呢?
假设这种情况,cois=[200, 100, 50, 20, 10],要凑出1000元,如果idx = 2
那么 [200(0张), 100(4张)],[200(1), 100(2)],[200(2), 100(0)]这些选择都会使得当前的aim = 600,
直接去递归就会产生大量重复计算。
而后面如何选出600的过程前面不需要关心,只要它给我返回结果数就行。
代码:
struct hash_pair {
template <class T1, class T2>
size_t operator()(const pair<T1, T2>& p) const
{
auto hash1 = hash<T1>{
}(p.first);
auto hash2 = hash<T2>{
}(p.second);
return hash1 ^ hash2;
}
};
class Solution {
//注意 unordered_map无法使用pair作为key,需要手动传入一个hash函数
//map可以,但是查找效率低
unordered_map<pair<int,int>,int,hash_pair> cache;
int size;//记录硬币个数
vector<int> coin;
public:
int change(int amount, vector<int>& coins)
{
size = coins.size();
coin = coins;
return dfs(amount, 0);
}
int dfs(int amount, int index)
{
if (cache.find({
amount,index}) != cache.end()) return cache[{
amount, index}];
if (amount == 0) return 1;
if (index >= size) return 0;
int ret = 0;
//对每一张硬币选择不超过当前背包容量的若干张
for (int i = 0; i * coin[index] <= amount; i++)
ret += dfs(amount - i * coin[index], index + 1);
cache[{
amount, index}] = ret;
return ret;
}
};