【MySQL】数据库索引原理 | 索引数据结构 | B+Tree

数据库索引原理 | 索引数据结构 | B+Tree

---

---

一. 数据库索引简介

索引是帮助 MySQL 高效获取数据的，已排好序的一种数据结构。一般采用的数据结构有：

• 二叉排序树
• 红黑树
• Hash 表
• B-Tree
• B+Tree

在通常情况下，若要在 7 条记录中查询某条记录，按顺序表的查询效率较低。例如，查找 7 条记录中的 id 为 5 的值，按顺序查询要查询 5 次。若以二叉排序树来作为索引的数据结构，如下例：

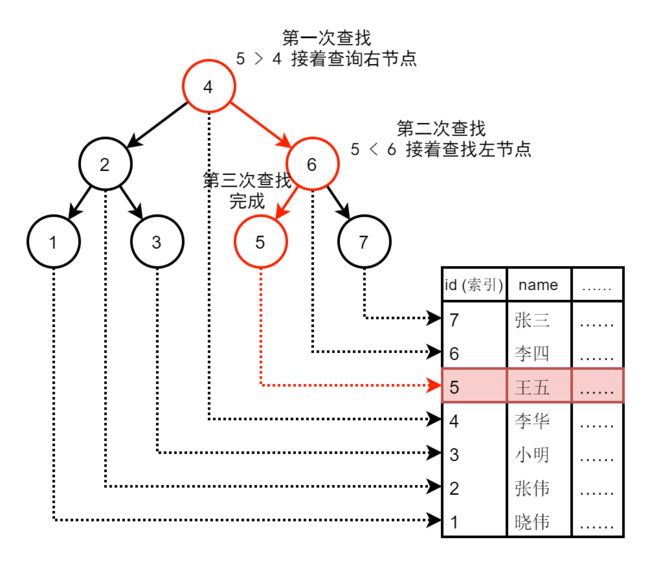
图1. 二叉排序树作为索引数据结构的查询

id 为索引，此时仅需要查找 3 次。可见索引在优化查询方面的巨大价值。

但是以二叉排序树作为检索数据结构在也有诸多缺点。例如：

• 在插入新值后二叉树需要重新平衡才能保证索引的作用

  二叉排序树若不进行平衡，则不能起到优化查询的目的。若要进行平衡，则会产生格外的性能开销。

  例如，连续插入 id 值递增的数据，二叉树若不平衡，则和链表无异，查询效率也和顺序查询相同。

  

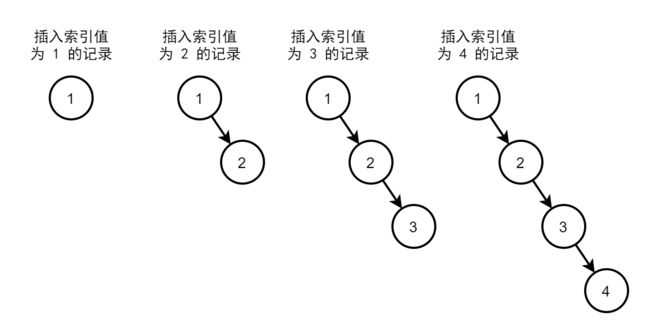
  图2. 二叉排序树索引的连续递增插入

  提示

  ---

  若不清楚为什么新插入的值都链接到右侧，可以去回顾数据结构二叉排序树。

• 不适合做范围查找

  如果在图1. 中情况做范围查询 id 大于 2 的值，查找过程会相对复杂，开销大。

• 随着数据量的增大，二叉树高度越来越高，查找效率下降

  在第一点中提到必须平衡二叉树后才能起优化查询的作用。假设二叉树每次插入后都进行平衡，当数据量达到上十万时，二叉树的高度也会变得非常大，此时无论是平衡二叉树的操作，还是查找二叉树的操作开销都会非常大。

---

二. 红黑树 与 B-Tree

在上一节中介绍了索引如何提高查询效率。从中可见，选取合适的数据结构至关重要。我们继续看两种可用的数据结构 —— 红黑树 与 B-Tree。

1. 红黑树

红黑树是一种特殊 AVL 树（平衡二叉树），也称平衡二叉 B 树。其操作的插入与删除都会使得二叉树保持平衡，从而避免图2. 中的情况。

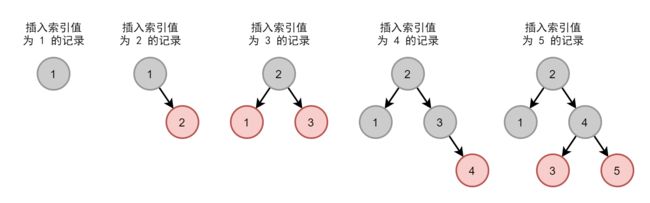
图3. 红黑树索引的连续等增插入

此时相比按顺序查找 5 次找到索引值为 5，红黑树只需要查找 3 次。但是红黑树依然没有解决范围查找与海量数据效率低下的问题。

2. B-Tree

B-Tree 又称多路搜索树，其插入与删除都可以保证平衡，特别的，B-Tree 是 “多叉” 的，而不是二叉的。

为什么想到 B-Tree 树呢？正是因为它是 “多叉” 的。这意味相比二叉树，其一个节点可以链接的节点多于 2（节点的度大于 2），这样节点数相同的情况下，B-Tree 的高度更小，查找的次数也更小。

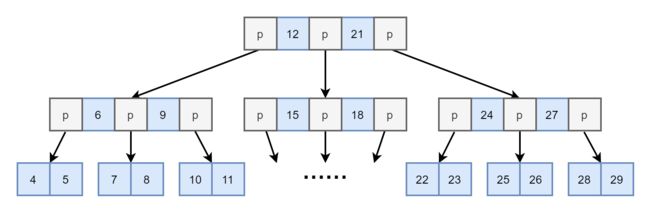
图4. 高度为 3 的B-Tree（图中的 p 为指向下一节点的指针）

如图4. 所示，这是一颗高度为 3 ，每个节点可以容纳 3 个值的 B-Tree，一共容纳 29 个值。相比高度为 3 的满二叉树只能容纳 7 个值。

此时若假设，数据库表中有 29 条记录，以 id 为索引值分别建二叉树（考虑最理想情况下为平衡二叉树）和 B-Tree 的索引，并查找索引值 28。二叉树的高度为 5，则查找 28 需要进行 5 次查找，而 B-Tree 如图4. 高度为 3，查找 28 仅需要进行 3 次查找。

可见，B-Tree 相对容量大，相对高度增长慢，极大的改善了随着数据量的增大，二叉树高度越来越高，查找效率下降的问题。并且其插入删除也是可保持平衡的。现在唯一的问题就是无法支持范围查询。

提示

---

• 为什么有 29 个值节点的平衡二叉树树高度为 5 ？
  平衡二叉树除了最后一层，其他层都是满的，所以最后一层之外的节点总数必为 2 ⁿ，n 为除了最后一层外的层数。因此有，2⁴ = 16，2⁵ = 32，2⁴ < 29 < 2⁵，因此 29 个节点构成的平衡二叉树高度大于 4 但不满 5，高度为 5。

  

  图5. 29个节点的平衡二叉树

• B-Tree 是如何查找节点 28 的？

1. 用 28 和根节点（注意，B-Tree 中的树节点容纳了多个值！）中的 12 比较，28 大。28 和 21 比较，28 大，由根节点中的右节点指针查询下一节点。
2. 在根节点的右节点中，用 28 和 24 比较，28 大。用 28 和 27 比较，28 大，因此根据当前节点的右节点指针继续访问右节点。
3. 在下一层节点中，找到所查询的值 28，查询完成。

   图6. 29 个节点的 B-Tree

---

三. MySQL 的完美解决方案 —— B+Tree

B+Tree 是应对数据库表索引的完美数据结构。其在保证 B-Tree 的基础上进行了改造，能够支持范围查询。

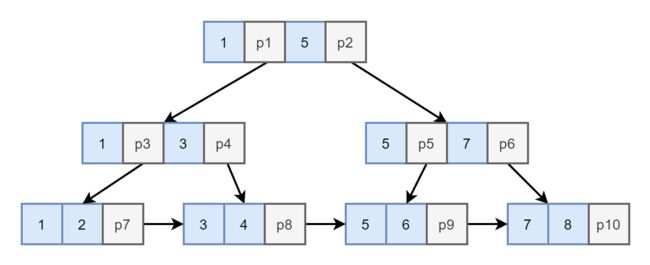
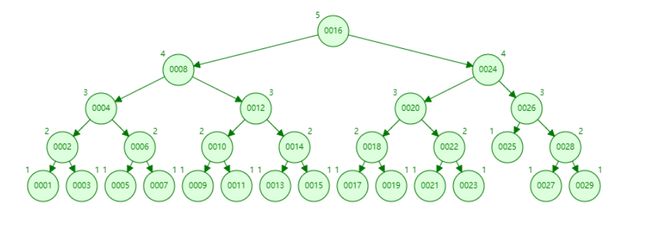
图7. B+Tree

如图7. 所示，B+Tree 有以下特征：

• 节点值冗余，叶节点包含树中所有的值
  我们可以看到根节点中的值 1 和 5 都出现了 3 次；3、5、7都出现了两次。这些冗余值将整个树中各个节点的值 “传导” 到了叶节点上。这使得叶节点中包含了树中所有的值
• 叶节点包含一个指向同层相邻节点的指针
  我们可以看到叶节点包含了一个指针，指向同层的相邻节点。
• 叶节点按大小顺序排列
  我们可以发现最后一层的叶节点都是按照大小顺序排列好的。

接下来我们对如图7. 的 B-Tree 树进行查询。

• B-Tree 查找索引值 4

1. 从根节点开始，4 和 1 比较，4 大。4 和 5 比较，4 小，由 p1 查询下一节点。
2. 4 和 3 比较，4 大，由 p4 查询下一节点。
3. 查询到 4，查询完成。

• B-Tree 查询大于 4 的所有索引值

1. 查询索引值 4
2. 由该索引值所在的叶节点的指针向后查询，得到所有大于 4 的索引值。

至此，B+Tree 解决了在第一节中提出的，二叉树作为索引数据结构的所有问题。

---

四. 索引下的 SQL 查询过程

接下来我们理解索引情况下具体的 SQL 查询过程。

首先，我们要清楚，数据表文件是存储在磁盘中的，而不是内存中。并且不能说我们直接将磁盘中所有的数据全一次性加载入内存，这样不仅耗费内存而且加载时间很长。

而对于索引本身，也是存储在磁盘中的。索引所占的大小也可以很大，不能一次性加载入内存。数据库开始只加载索引的根节点入内存。

假设索引数据结构是 B-Tree（如下图8.），我们来进行一次查询。

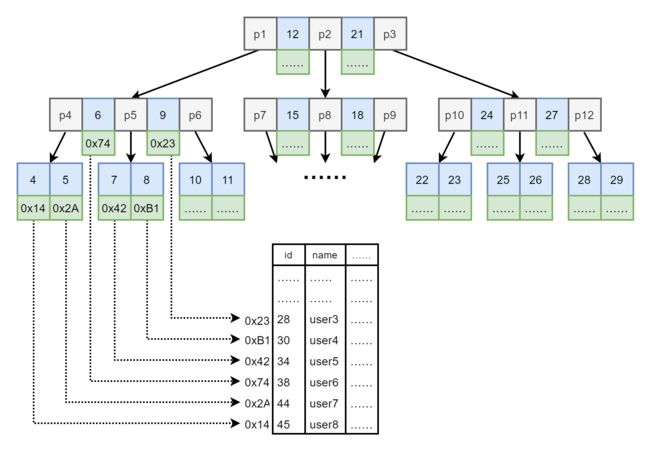
图8. B-Tree 索引下的数据表存储

• 进行查询 select * from index_id = 9

1. 内存加载根节点。
2. 由 9 和根节点的 12 比较，9 小。由指针 p1 从磁盘中读取下一节点入内存。
3. 在下一节点中进行比较。9 和 6 比较，8 大。9 和 9 比较，找到索引值。
4. 找到对应的索引值，获取其对应的数据表记录磁盘地址，图中为 0x23。
5. 根据 0x23 磁盘地址找到查询的记录，查询成功。

可见进行了 2 次（不包括根节点加载）磁盘读取就得到了查询的记录。

但是毕竟是 B-Tree，不支持范围查询，所以我们接下来继续看 B+Tree 的查询过程。

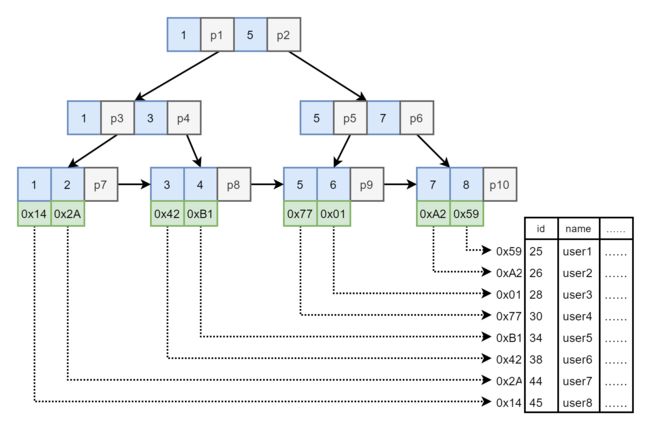
图9. B+Tree 索引下的 SQL

• 进行查询 select * from index_id = 3

1. 内存加载根节点。
2. 由 3 和根节点的 1 比较，3 大。由 4 和根节点的 5 比较，3 小。由 p1 指针从磁盘中读取下一节点入内存。
3. 在下一节点进行比较。3 和 3 比较相等，但是根据 p4 指针继续从磁盘中读取下一节点入内存。
4. 在下一节点中找到索引值为 3 的节点，并获取其对应的数据表记录磁盘地址，图中为 0x42。
5. 根据 0x42 读取磁盘中的数据表记录，查询成功。

注意

---

B+Tree 为索引数据结构的情况下与 B-Tree不同。
B-Tree 中每个节点都保存了对应的磁盘地址，而 B+Tree 中只有叶节点才保存了磁盘地址数据。
所以即便在非叶节点找到了对应的索引值，也必须向下加载节点，直至叶节点，再获取磁盘地址数据。

• 进行查询 select * from index_id > 4

1. 和上一点中所描述，查找索引值为 4 的节点。
2. 由该节点中的 p8 指针向后查找相邻节点，获取索引值 为 5、6 的磁盘地址。再继续由 p9 指针查找下一相邻节点，获取索引值为 7、8 的磁盘地址。
3. 根据获取的 5、6、7、8 索引值对应的磁盘地址获取磁盘中的数据表记录，查询成功。

可见对于如图9. 中的 B+Tree，1 - 8 索引值的查找全部都需要加载 3 次（不包括根节点加载）磁盘才能完成查询。

那这不是比 B-Tree 查找效率低吗？

实际上不是，图9. 是为了方便描述而设计的 B+Tree，其已经类似于二叉树，因为每个节点的度为 2；并且每个节点也只保存了两个索引值。但实际情况下，我们可以使得每个节点拥有多的分支，保存更多的索引值，如图10. 。此时对于上万条记录的索引存入其中，读取磁盘也仅需 3 次。

图10. B+Tree 索引通常情况

---

五. MySQL 数据库引擎 MyISAM 与 InnoDB

MySQL 两种常用的数据库引擎 MyISAM 和 InnoDB 都是使用 B+Tree 为索引结构的。但其不同在于，MyISAM 是非聚簇索引，而 InnoDB 是聚簇索引。

我们从 MyISAM 引擎的数据表文件与 InnoDB 引擎的数据表文件进行比较。

图11. MyISAM 引擎的数据表文件与 InnoDB 引擎的数据表文件

MyISAM 的数据表有三个文件，后缀分别为 .frm、.MYD、.MYI。而 InnoDB 的数据表有两个文件，后缀分别为 .frm、.ibd。这里 .frm 文件不做讨论。

1. MyISAM 非聚簇索引

在本文中，图1. 、图8. 、图9. 展示的都是非聚簇索引的情况。以图9. 为例。

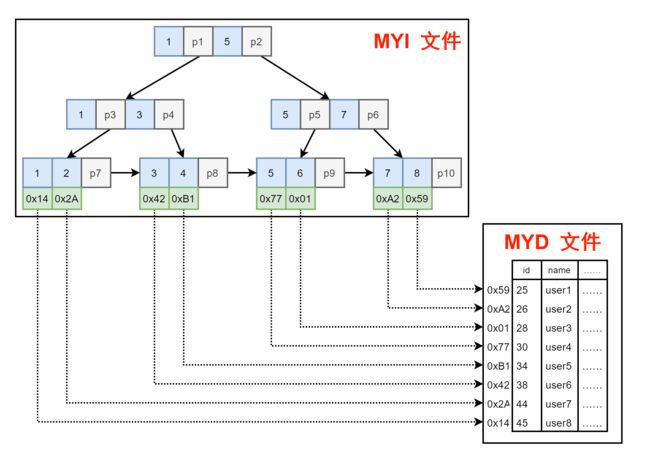
图12. MyISAM 文件情况

在 MYI 文件中，存储的其实就是索引结构 B+Tree，而数据表数据则都存储在 MYD 文件中。

所以在 MyISAM 的数据表进行检索查询时，先得到 MYI 文件中查，再到 MYD 中拿。这就是非聚簇索引。

2. InnoDB 聚簇索引

InnoDB 的数据表文件除了 .frm 只有一个 .ibd 文件。这个文件相当于将 MyISAM 的两个文件结合了。如图13. 在索引值下，直接接上了数据表的记录。

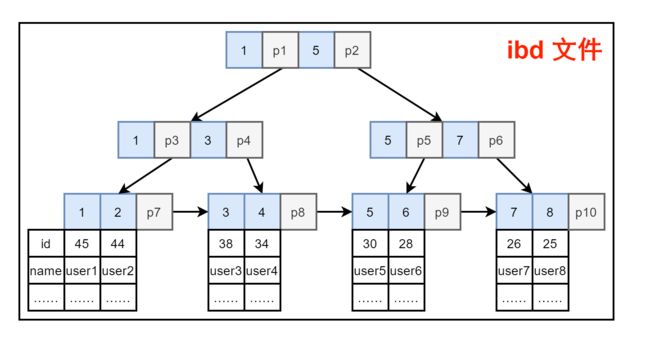
图13. InnoDB 文件情况

这样的情况下，相比 MyISAM 两个文件分开，要先查再拿。InnoDB 聚簇索引在查找到之后就可以直接拿到数据记录，效率更高。

MyISAM 与 InnoDB 的其他不同

---

• MyISAM 在 MySQL 5.5 之前是默认数据库引擎，之后 InnoDB 为默认的数据库引擎
• MyISAM 可以不设立主键，InnoDB 必须建立主键。
• MyISAM 不支持事务，InnoDB 支持事务。
• MyISAM必须依靠操作系统来管理读取与写入的缓存，而InnoDB则是有自己的读写缓存管理机制。
• InnoDB 支持外键，而 MyISAM 不支持。
  
  

MyISAM 和 InnoDB 的区别还有很多，这里只列举部分，读者可以多查找资料。

---

其他相关文章

文章名称	更新时间
数据库索引原理与索引数据结构	2021-05-23
数据库索引优化	准备中

---

文章内容来自个人学习总结 欢迎指出本文中存在的问题 未经本人同意禁止转载，不得用于商业用途