5.8 拉普拉斯算子和拉普拉斯矩阵,图拉普拉斯算子推导 意境级讲解
文章目录
-
- 拉普拉斯算子
- 图函数
-
- 图函数的梯度
- 拉普拉斯算子与拉普拉斯矩阵
- 拉普拉斯矩阵的重要性质
- 图拉普拉斯算子推导
-
- 1、图像普拉斯算子
- 2、图普拉斯算子推导
- 拉普拉斯矩阵归一化
-
- 随机归一化推导
- 对称归一化推导
- 参考
拉普拉斯矩阵为舍被定义成 L = D − A L=D-A L=D−A ?这玩意为什么冠以拉普拉斯之名?为什么和图论有关的算法如此喜欢用拉普拉斯矩阵和它的特征值?
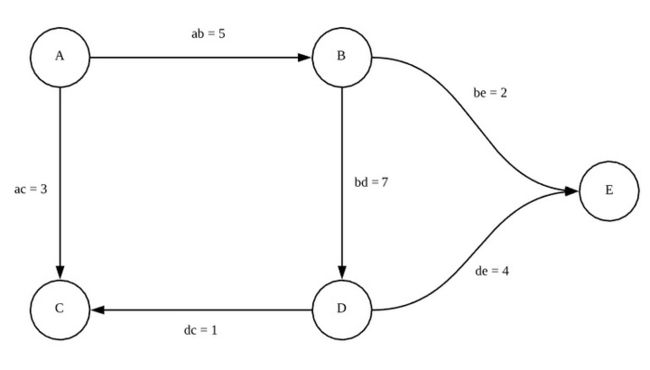
接触到了图论中的Laplacian矩阵,定义为 L = D − A , L L=D-A, L L=D−A,L 是Laplacian矩阵, D D D 是顶点的度矩阵, A A A 是图的邻接矩阵。看图1的示例,就能很清楚知道 L L L 的计算过程。

图 1 图1 图1
要讲拉普拉斯矩阵,就要从拉普拉斯算子讲起,要讲拉普拉斯算子,就要从散度讲起~
散度的基本知识可以看看:6.1通量和散度_炫云云
图的基本知识可以看看:
图01—图的基本概念与模型_炫云云
图02—存储结构,邻接矩阵,关联矩阵,权矩阵,邻接表,十字链表_炫云云
拉普拉斯算子
根据定义,函数 f f f 的拉普拉斯算子 ∇ 2 f \nabla^{2} f ∇2f 又可以写成 ∇ ⋅ ∇ f \nabla \cdot \nabla f ∇⋅∇f, 其被定义为函数 f f f 梯度的散度。
Δ f = ∇ 2 f = ∇ ⋅ ∇ f = d i v ( g r a d f ) (1) \Delta f=\nabla^{2} f=\nabla \cdot \nabla f=d i v( grad f)\tag{1} Δf=∇2f=∇⋅∇f=div(gradf)(1)
那么这又是什么意思呢?
我们知道, 在直角坐标系下,一个函数 f ( x , y , z ) f(x, y, z) f(x,y,z) 在 ( x 0 , y 0 , z 0 ) \left(x_{0}, y_{0}, z_{0}\right) (x0,y0,z0) 处的梯度是一个向量
( ∂ f ∂ x , ∂ f ∂ y , ∂ f ∂ z ) ∣ x = x 0 , y = y 0 , z = z 0 (2) \left.\left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}\right)\right|_{x=x_{0}, y=y_{0}, z=z_{0}}\tag{2} (∂x∂f,∂y∂f,∂z∂f)∣∣∣∣x=x0,y=y0,z=z0(2)
于是函数 f f f 的梯度函数
∇ f = ∂ f ∂ x ⋅ i ⃗ + ∂ f ∂ y ⋅ j ⃗ + ∂ f ∂ z ⋅ k ⃗ (3) \nabla f=\frac{\partial f}{\partial x} \cdot \vec{i}+\frac{\partial f}{\partial y} \cdot \vec{j}+\frac{\partial f}{\partial z} \cdot \vec{k}\tag{3} ∇f=∂x∂f⋅i+∂y∂f⋅j+∂z∂f⋅k(3)
就构成了一个在三维空间下的向量场。那么散度在笛卡尔坐标系下的表示法:
Δ f = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 + ∂ 2 f ∂ z 2 (4) \Delta f=\frac{\partial^{2} f}{\partial x^{2}}+\frac{\partial^{2} f}{\partial y^{2}}+\frac{\partial^{2} f}{\partial z^{2}}\tag{4} Δf=∂x2∂2f+∂y2∂2f+∂z2∂2f(4)
n n n 维形式 Δ = ∑ i ∂ 2 ∂ x i 2 \Delta=\sum_{i} \frac{\partial^{2}}{\partial x_{i}^{2}} Δ=∑i∂xi2∂2
于是平, 我们对这一向量场 ∇ f \nabla f ∇f 求散度 ∇ ⋅ ∇ f \nabla \cdot \nabla f ∇⋅∇f, 即得到了 f f f 的拉普拉斯算子 ∇ 2 f \nabla^{2} f ∇2f 。
为什么要这样做呢?
让我们想像一座山,根据梯度的定义,在山峰周围,所有的梯度向量向此汇聚,所以每个山峰处的拉普拉斯算子为负;而在山谷周围,所有梯度从此发散,所以每个山谷处的拉普拉斯算子为正。所以说,对于一个函数,拉普拉斯算子实际上衡量了在空间中的每一点处,该函数梯度是倾向于增加还是减少。
描述物理系统最优美的公式之一拉普拉斯方程, ∇ 2 f = 0 \nabla^{2} f=0 ∇2f=0, 大家可以想一想, 这一公式表 达了物理系统怎么样的特征呢?
图函数
我们知道,互相连接的节点可以构成一张图,其中包含所有点构成的集合 V V V, 和所有边构成的 集合 E E E 。
对于实数域上的函数 y = f ( x ) y=f(x) y=f(x), 我们可以理解为一种对于 x x x 的映射,将每个可能的 x ∈ X x \in X x∈X 映射到一个对应的 y ∈ Y y \in Y y∈Y 上 ( f : X → Y ) (f: X \rightarrow Y) (f:X→Y) 。
相应地, 我们也可以定义一个图函数 F G : V → R F_{G}: V \rightarrow R FG:V→R, 使得图上的每一个节点 v ∈ V v \in V v∈V, 都被 映射到一个实数 R R R 上。
比如说,假设我们有一个这样的社交网络图谱:
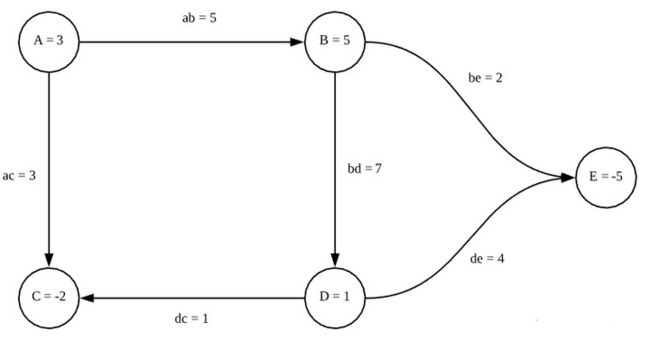
假设说每一条边的权值对应两个人之间信息的流通程度。现在我们想要分析这个社交网络上的信息传播,我们不仅需要知道信息流通的程度,我们还要知道每个人发动态的活跃程度,于是我们现在给这个图一个函数 F G F_{G} FG, 使得:
F G ( A ) = 3 , F G ( B ) = 5 , F G ( C ) = − 2 , F G ( D ) = 1 , F G ( E ) = − 5 F_G(A) = 3, F_G(B) = 5, F_G(C) = -2, F_G(D) = 1, F_G(E) = -5 FG(A)=3,FG(B)=5,FG(C)=−2,FG(D)=1,FG(E)=−5
这里的负数似乎可以理解为, C C C 和 E E E 是谣言终结者, 可以阻止信息的传播
那么我们得到这样一张图:
图函数的梯度
我们定义了图论的函数,那么应该如何给图论下的函数定义梯度呢?
我们记得,梯度的意义在于,衡量函数在每一个点处,在每个正交方向上的变化, 如 f ( x , y , z ) f(x, y, z) f(x,y,z) 的梯度在 x x x 方向的分量
∂ f ∂ x = f ( x + d x ) − f ( x ) ( x + d x ) − x (5) \frac{\partial f}{\partial x}=\frac{f(x+d x)-f(x)}{(x+d x)-x} \tag{5} ∂x∂f=(x+dx)−xf(x+dx)−f(x)(5)
在图论中,我们认为一个节点沿着每一条边通向它的相邻节点,而每两条边之间互相并没有什么关系,也就是说我们认为这个节点的每一条边互相都是正交的。
并且对于两个节点, 我们定义其距离 d d d 为其边权值的倒数 (比如上面社交网络的例子, 我们可以认为, 两个人的信息流通程度越低, 两个人的友谊就 “越远")
那么对于一个节点 v 0 v_{0} v0, 我们认为其梯度在一条通向 v 1 v_{1} v1 的边 e 01 e_{01} e01 上的分量为
( F G ( v 0 ) − F G ( v 1 ) ) d 01 = ( F G ( v 0 ) − F G ( v 1 ) ) ⋅ e 01 (6) \frac{\left(F_{G}\left(v_{0}\right)-F_{G}\left(v_{1}\right)\right)}{d_{01}}=\left(F_{G}\left(v_{0}\right)-F_{G}\left(v_{1}\right)\right) \cdot e_{01}\tag{6} d01(FG(v0)−FG(v1))=(FG(v0)−FG(v1))⋅e01(6)
( \left(\right. ( 其中 d 01 d_{01} d01 为 v 0 v_{0} v0 到 v 1 v_{1} v1 的距离),
详细的图表示,请看:图02—存储结构,邻接矩阵,关联矩阵,权矩阵,邻接表,十字链表_炫云云
为了计算梯度,我们给出一个这样的矩阵:
每一行代表一个点, 每一列代表一条边, 使得对于每个点每条边, 如果该条边从该点发射出 去, 且权值为 X X X, 则将矩阵中对应的这一元素置为 − X -X −X ,如果该条边指向该点,则将对 应的元素置为 + X +X +X
具体到上面社交网络的例子,我们有相应的矩阵 K G K_{G} KG :
我们又有关于图函数 F G F_{G} FG 的列向量 f G f_{G} fG :
我们试着计算 K G T × f G K^T_G \times f_G KGT×fG:
( − 5 5 0 0 0 − 3 0 3 0 0 0 − 7 0 7 0 0 0 1 − 1 0 0 0 0 − 4 4 0 − 2 0 0 2 ) × ( 3 5 − 2 1 − 5 ) = ( 10 − 15 − 28 − 3 − 24 − 20 ) \begin{pmatrix} -5 & 5 & 0 & 0 & 0 \\ -3 & 0 & 3 & 0 & 0 \\ 0 & -7 & 0 & 7 & 0 \\ 0 & 0 & 1 & -1 & 0 \\ 0 & 0 & 0 & -4 & 4 \\ 0 & -2 & 0 & 0 & 2 \\ \end{pmatrix} \times \begin{pmatrix} 3 \\ 5 \\ -2 \\ 1 \\ -5 \\ \end{pmatrix} = \begin{pmatrix} 10 \\ -15 \\ -28 \\ -3 \\ -24 \\ -20 \\ \end{pmatrix} ⎝⎜⎜⎜⎜⎜⎜⎛−5−3000050−700−2030100007−1−40000042⎠⎟⎟⎟⎟⎟⎟⎞×⎝⎜⎜⎜⎜⎛35−21−5⎠⎟⎟⎟⎟⎞=⎝⎜⎜⎜⎜⎜⎜⎛10−15−28−3−24−20⎠⎟⎟⎟⎟⎟⎟⎞
经过观察我们可以知道,最后计算结果的向量, 即是整个图 G G G 在 F G F_{G} FG 函数上的梯度 ∇ G F G \nabla_{G} F_{G} ∇GFG 其中每一行,为该梯度在一条边上的分量。
所以对于图 G G G, 我们有 ∇ G = K G T \nabla_{G}=K_{G}^{T} ∇G=KGT,使得 ∇ G F G = K G T × f G \nabla_{G} F_{G}=K_{G}^{T} \times f_{G} ∇GFG=KGT×fG
拉普拉斯算子与拉普拉斯矩阵
我们记得在函数中,拉普拉斯算子的定义为函数梯度的散度,即每一点上其梯度的增加/减少,那么对于图函数,其每一“点”即为每个“节点”,其梯度的散度该怎么定义呢?
我们几乎可以立刻可以想到,图函数每一点上梯度的散度,即是从该节点射出的梯度,减去射入该节点的梯度,那么我们几乎又可以立即想到,根据这样的定义去计算散度,只要把原来的梯度再左乘一个这样的矩阵就可以啦:
每一行代表一个点, 每一列代表一条边, 使得对于每个点每条边, 如果该条边从该点发射出 去,则将矩阵中对应的这一元素置为 − 1 -1 −1 ,如果该条边指向该点,则将对应的元素置为 1
命名这一矩阵为 K G ′ K_{G}^{\prime} KG′
也就是说,我们把 K G K_{G} KG 的每个元素,正的变成1,负的变成-1, 就得到了 K G ′ K_{G}^{\prime} KG′
( − 1 − 1 0 0 0 0 1 0 − 1 0 0 − 1 0 1 0 1 0 0 0 0 1 − 1 − 1 0 0 0 0 0 1 1 ) × ( 10 − 15 − 28 − 3 − 24 − 20 ) = ( 5 58 − 18 − 1 − 44 ) \begin{pmatrix} -1 & -1 & 0 & 0 & 0 & 0 \\ 1 & 0 & -1 & 0 & 0 & -1 \\ 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & -1 & -1 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 \\ \end{pmatrix} \times \begin{pmatrix} 10 \\ -15 \\ -28 \\ -3 \\ -24 \\ -20 \\ \end{pmatrix} = \begin{pmatrix} 5 \\ 58 \\ -18 \\ -1 \\ -44 \end{pmatrix} ⎝⎜⎜⎜⎜⎛−11000−101000−1010001−10000−110−1001⎠⎟⎟⎟⎟⎞×⎝⎜⎜⎜⎜⎜⎜⎛10−15−28−3−24−20⎠⎟⎟⎟⎟⎟⎟⎞=⎝⎜⎜⎜⎜⎛558−18−1−44⎠⎟⎟⎟⎟⎞
那么, 整个图 G G G 在 F G F_{G} FG 函数上的散度
∇ G 2 F G = K G ′ × ∇ G F G = K G ′ × ( K G T × f G ) = ( K G ′ K G T ) f G (7) \begin{aligned} \nabla_{G}^{2} F_{G} &=K_{G}^{\prime} \times \nabla_{G} F_{G} \\ &=K_{G}^{\prime} \times\left(K_{G}^{T} \times f_{G}\right) \\ &=\left(K_{G}^{\prime} K_{G}^{T}\right) f_{G} \end{aligned}\tag{7} ∇G2FG=KG′×∇GFG=KG′×(KGT×fG)=(KG′KGT)fG(7)
于是我们得到了图论函数的 拉 普 拉 斯 算 子 \large\color{#70f3ff}{\boxed{\color{green}{ 拉普拉斯算子}}} 拉普拉斯算子 ∇ 2 = K G ′ K G T , \nabla^{2}=K_{G}^{\prime} K_{G}^{T} , ∇2=KG′KGT, 即我们常说的 拉 普 拉 斯 矩 阵 \large\color{#70f3ff}{\boxed{\color{green}{ 拉普拉斯矩阵}}} 拉普拉斯矩阵。
注意在我们上面的范例中,将任意一条边的方向反转, 等价于在 K G K_{G} KG 的一列上乘以 − 1 , -1 , −1, 这 种情况下最终 K G ′ K G T K_{G}^{\prime} K_{G}^{T} KG′KGT 不会改变, 也就是说拉普拉斯矩阵的值与图中每一条边的方向无关,所以拉普拉斯矩阵一般用来表述无向图
计算 K G ′ K G T K_{G}^{\prime} K_{G}^{T} KG′KGT 的值, 我们得到矩阵:
( 8 − 5 − 3 0 0 − 5 14 0 − 7 − 2 − 3 0 4 − 1 0 0 − 7 − 1 12 − 4 0 − 2 0 − 4 6 ) \begin{pmatrix} 8 & -5 & -3 & 0 & 0 \\ -5 & 14 & 0 & -7 & -2 \\ -3 & 0 & 4 & -1 & 0 \\ 0 & -7 & -1 & 12 & -4 \\ 0 & -2 & 0 & -4 & 6 \\ \end{pmatrix} ⎝⎜⎜⎜⎜⎛8−5−300−5140−7−2−304−100−7−112−40−20−46⎠⎟⎟⎟⎟⎞
注意到这一对称矩阵,对角线即是每个点的度,而其余的元素,则是负的邻接矩阵,于是乎我们得到了拉普拉斯矩阵的经典算式:
L = D − A L = D - A L=D−A
定义 D D D 是 N × N N \times N N×N 的度数矩阵(degree matrix)
D ( i , j ) = { d i if i = j 0 otherwise D(i, j)=\left\{\begin{array}{ll}d_{i} & \text { if } i=j \\ 0 & \text { otherwise }\end{array}\right. D(i,j)={ di0 if i=j otherwise
定义 A A A 为 N × N N \times N N×N 邻接矩阵(adjacency matrix)
A ( i , j ) = { d i if x i ∼ x j 0 otherwise A(i, j)=\left\{\begin{array}{ll}d_{i} & \text { if } x_{i} \sim x_{j} \\ 0 & \text { otherwise }\end{array}\right. A(i,j)={ di0 if xi∼xj otherwise
则在图3中,
D = ( 8 0 0 0 0 0 14 0 0 0 0 0 4 0 0 0 0 0 12 0 0 0 0 0 6 ) , A = ( 0 5 3 0 0 5 0 0 7 2 3 0 0 1 0 0 7 1 0 4 0 2 0 4 0 ) D=\begin{pmatrix} 8 & 0 & 0 & 0 & 0 \\ 0 & 14 & 0 & 0 & 0 \\ 0& 0 & 4 & 0 & 0 \\ 0 & 0 & 0 & 12 & 0 \\ 0 & 0 & 0 & 0 & 6 \\ \end{pmatrix},A=\begin{pmatrix} 0 & 5 & 3 & 0 & 0 \\ 5 & 0 & 0 & 7 & 2 \\ 3 & 0 & 0 & 1 & 0 \\ 0 & 7 & 1 & 0 & 4 \\ 0 & 2 & 0 & 4 & 0 \\ \end{pmatrix} D=⎝⎜⎜⎜⎜⎛800000140000040000012000006⎠⎟⎟⎟⎟⎞,A=⎝⎜⎜⎜⎜⎛0530050072300100710402040⎠⎟⎟⎟⎟⎞
所以
L = D − A = K G ′ K G T (8) L = D - A=K_G'K_G^T\tag{8} L=D−A=KG′KGT(8)
拉普拉斯矩阵的重要性质
拉普拉斯矩阵之所以如此常用,是因为其一大重要性质: 拉普拉斯矩阵的 n n n 个特征值 λ 1 , λ 2 , … , λ n \lambda_{1}, \lambda_{2}, \ldots, \lambda_{n} λ1,λ2,…,λn 都是非负值, 且有 0 = λ 1 ≤ λ 2 ≤ … ≤ λ n 0=\lambda_{1} \leq \lambda_{2} \leq \ldots \leq \lambda_{n} 0=λ1≤λ2≤…≤λn
同时,我们引入关于矩阵 L L L 和 h h h 的瑞利商的概念: R ( L , h ) = h ∗ L h h ∗ h R(L, h)=\frac{h^{*} L h}{h^{*} h} R(L,h)=h∗hh∗Lh
其中 h ∗ h^{*} h∗ 为 h h h 的共轭矩阵, 对于 h h h 为实数矩阵的情况下 h ∗ = h T h^{*}=h^{T} h∗=hT
而通过拉格朗日乘子法可以得出,瑞利熵的一个非常重要的特点就是: 瑞丽熵的最大值,等于 L L L 的最大特征值,瑞利熵的最小值,等于 L L L 的最小特征值
再看看图算法中对于拉普拉斯矩阵 L L L 的运算中常常出现的 f T L f f^{T} L f fTLf ,结合上文所述的拉普拉斯矩阵的重要性质,那么拉普拉斯矩阵在各种图算法中的应用,想必大家也能够理解啦~
图拉普拉斯算子推导
主要是以下3种:
- L = D − A L=D-A L=D−A 定义的图拉普拉斯算子
- L rw = D − 1 L L^{\text {rw}}=D^{-1} L Lrw=D−1L ,随机归一化图拉普拉斯算子
- L sn = D − 1 2 L D − 1 2 L^{\text {sn }}=D^{-\frac{1}{2}} L D^{-\frac{1}{2}} Lsn =D−21LD−21,对称归一化图拉普拉斯算子
本节讲解第一种图拉普拉斯算子是怎么由来的,归一化见下一节。
1、图像普拉斯算子
图像是一种离散数据,那么其拉普拉斯算子必然要进行离散化。
从导数定义说起
f ′ ( x ) = δ f ( x ) δ x ≈ f ( x + 1 ) − f ( x ) \begin{aligned} f'(x) &= \frac {\delta f(x)}{\delta x}\\ &\approx f(x+1)-f(x)\\ \end{aligned}\\ f′(x)=δxδf(x)≈f(x+1)−f(x)
那么:
δ 2 f ( x ) δ x 2 = f ′ ′ ( x ) ≈ f ′ ( x ) − f ′ ( x − 1 ) ≈ f ( x + 1 ) − f ( x ) − ( f ( x ) − f ( x − 1 ) ) = f ( x + 1 ) + f ( x − 1 ) − 2 f ( x ) (9) \begin{aligned} \frac {\delta^2 f(x)}{\delta x^2} &= f''(x) \\ &\approx f'(x)-f'(x-1) \\ &\approx f(x+1)-f(x) - (f(x) - f(x-1))\\ &=f(x+1)+f(x-1)-2f(x) \end{aligned}\tag{9} δx2δ2f(x)=f′′(x)≈f′(x)−f′(x−1)≈f(x+1)−f(x)−(f(x)−f(x−1))=f(x+1)+f(x−1)−2f(x)(9)
结论1:二阶导数近似等于其二阶差分。
结论2:二阶导数等于其在所有自由度上微扰之后获得的增益。
一维函数其自由度可以理解为2,分别是+1和-1两个方向。
对于二维的图像来说,其有两个方向(4个自由度)可以变化,如图4所示,即如果对 ( x , y ) (x,y) (x,y)处的像素进行扰动,其可以变为四种状态 ( x + 1 , y ) (x+1,y) (x+1,y), ( x − 1 , y ) (x-1,y) (x−1,y), ( x , y + 1 ) (x,y+1) (x,y+1), ( x , y − 1 ) (x,y-1) (x,y−1)。当然了,如果将对角线方向也认为是一个自由度的话,会再增加几种状态 ( x + 1 , y + 1 (x+1,y+1 (x+1,y+1), ( x + 1 , y − 1 ) (x+1,y-1) (x+1,y−1), ( x − 1 , y + 1 ) (x-1,y+1) (x−1,y+1), ( x − 1 , y − 1 ) (x-1,y-1) (x−1,y−1),事实上图像处理上正是这种。再当然了,如果你认为对一个像素进行微扰可能变为任何一个像素,那它的自由度就是整个图片的像素数(不过这还叫微扰吗?)。其实结论差不多,就讨论四种状态。
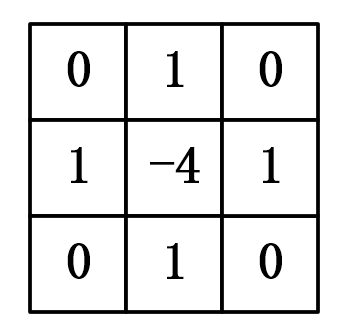
△ f = δ 2 f ( x , y ) δ x 2 + δ 2 f ( x , y ) δ y 2 ≈ f ( x + 1 , y ) + f ( x − 1 , y ) − 2 f ( x , y ) + [ f ( x , y + 1 ) + f ( x , y − 1 ) − 2 f ( x , y ) ] = f ( x + 1 , y ) + f ( x − 1 , y ) + f ( x , y + 1 ) + f ( x , y − 1 ) − 4 f ( x , y ) (10) \begin{aligned} \triangle f &=\frac {\delta^2 f(x,y)}{\delta x^2} + \frac {\delta^2 f(x,y)}{\delta y^2} \\ &\approx f(x+1,y)+f(x-1,y)-2f(x,y) + [f(x,y+1)+f(x,y-1)-2f(x,y)]\\ &= f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y) \end{aligned}\\\tag{10} △f=δx2δ2f(x,y)+δy2δ2f(x,y)≈f(x+1,y)+f(x−1,y)−2f(x,y)+[f(x,y+1)+f(x,y−1)−2f(x,y)]=f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)−4f(x,y)(10)
上式中每一项的系数就是拉普拉斯在二维图像中的卷积核:
现在用散度的概念解读一下:
- 如果 Δ f = 0 \Delta f=0 Δf=0 ,可以近似认为中心点 f ( x , y ) f(x, y) f(x,y) 的势和其周围点的势是相等的, f ( x , y ) f(x, y) f(x,y) 局部范围内不存在势差。所以该点无源.
- Δ f > 0 \Delta f>0 Δf>0, 可以近似认为中心点 f ( x , y ) f(x, y) f(x,y) 的势低于周围点, 可以想象成中心点如恒星一样 发出能量,补给周围的点,所以该点是正源
- Δ f < 0 \Delta f<0 Δf<0,可以近似认为中心点 f ( x , y ) f(x, y) f(x,y) 的势高于周围点, 可以想象成中心点如吸引子一样 在吸收能量, 所以该点是负源.
另一个角度,根据离散状态下拉普拉斯算子 (10) ,其计算了周围点与中心点的梯度差。当 f ( x , y ) f(x, y) f(x,y) 受到扰动之后,其 可能变为相邻的 f ( x − 1 , y ) , f ( x + 1 , y ) , f ( x , y − 1 ) , f ( x , y + 1 ) f(x-1, y), f(x+1, y), f(x, y-1), f(x, y+1) f(x−1,y),f(x+1,y),f(x,y−1),f(x,y+1) 之一,拉普拉斯算子得到的是对该点进行微小扰动后可能获得的增益 (或者说是总变化)。
2、图普拉斯算子推导
我们现在将这个结论推广到图: 假设具有 N N N 个节点的图 G G G, 此时以上定义的函数 f f f 不再是 二维,而是 N N N 维向量: f = ( f 1 , f 2 , … , f N ) f=\left(f_{1}, f_{2}, \ldots, f_{N}\right) f=(f1,f2,…,fN), 其中 f i f_{i} fi 为函数 f f f 在图中节点 i i i 处的函 数值。类比于 f ( x , y ) f(x, y) f(x,y) 在节点 ( x , y ) (x, y) (x,y) 处的值。如图5所示,对 i i i 节点进行扰动, 它可能变为任意一个与它相邻的节点 j ∈ N i , N i j \in N_{i}, N_{i} j∈Ni,Ni 表示节点 i i i 的一阶邻域节点。
图 5 图5 图5
我们上面已经知道拉普拉斯算子可以计算一个点到它所有自由度上微小扰动的增益,则通过图来表示就是任意一个节点 j j j 变化到节点 i i i 所带来的增益, 考虑图中边的权重相等 (简单说就是1) 则有:
Δ f i = ∑ j ∈ N i ( f i − f j ) (11) \Delta {f_i} = \sum\limits_{j \in {N_i}} {({f_i} - } {f_j})\tag{11} Δfi=j∈Ni∑(fi−fj)(11)
设边 E i j E_{i j} Eij 得权重为 W i j W_{i j} Wij , 则有:
Δ f i = ∑ j ∈ N i W i j ( f i − f j ) (12) \Delta f_{i}=\sum_{j \in N_{i}} W_{i j}\left(f_{i}-f_{j}\right) \tag{12} Δfi=j∈Ni∑Wij(fi−fj)(12)
由于当 W i j = 0 W_{i j}=0 Wij=0 时表示节点 i , j i, j i,j 不相邻,所以上式可以简化为 :
Δ f i = ∑ j ∈ N W i j ( f i − f j ) (13) \Delta {f_i} = \sum\limits_{j \in {N}} { {W_{ij}}({f_i} - } {f_j})\tag{13} Δfi=j∈N∑Wij(fi−fj)(13)
继续推导有:
Δ f i = ∑ j ∈ N w i j ( f i − f j ) = ∑ j ∈ N w i j f i − ∑ j ∈ N w i j f j = d i f i − w i : f (14) \begin{array}{l} \Delta {f_i} = \sum\limits_{j \in N} { {w_{ij}}({f_i} - {f_j})} \ \\= \sum\limits_{j \in N} { {w_{ij}}{f_i} - \sum\limits_{j \in N} { {w_{ij}}{f_j}} } \ \\= {d_i}{f_i} - {w_{i:}}f \end{array}\tag{14} Δfi=j∈N∑wij(fi−fj) =j∈N∑wijfi−j∈N∑wijfj =difi−wi:f(14)
其中 d i = ∑ j ∈ N w i j d_{i}=\sum_{j \in N} w_{i j} di=∑j∈Nwij 是顶点 i i i 的度
w i : = ( w i 1 , … , w i N ) w_{i:}=\left(w_{i 1}, \ldots, w_{i N}\right) wi:=(wi1,…,wiN) 是 N N N 维的行向量, f = ( f 1 ⋮ f N ) f=\left(\begin{array}{c}f_{1} \\ \vdots \\ f_{N}\end{array}\right) f=⎝⎜⎛f1⋮fN⎠⎟⎞ 是 N N N 维的列向量:
w i : f w_{i:} f wi:f 表示两个向量的内积。
对于所有的 N N N 个节点有:
Δ f = ( Δ f 1 ⋮ Δ f N ) = ( d 1 f 1 − w 1 : f ⋮ d N f N − w N : f ) = ( d 1 ⋯ 0 ⋮ ⋱ ⋮ 0 ⋯ d N ) f − ( w 1 : ⋮ w N : ) f = diag ( d i ) f − W f = ( D − W ) f = L f \begin{array}{l} \Delta f=\left(\begin{array}{c} \Delta f_{1} \\ \vdots \\ \Delta f_{N} \end{array}\right)=\left(\begin{array}{c} d_{1} f_{1}-w_{1:} f \\ \vdots \\ d_{N} f_{N}-w_{N:} f \end{array}\right) \\ =\left(\begin{array}{ccc} d_{1} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & d_{N} \end{array}\right) f-\left(\begin{array}{c} w_{1:} \\ \vdots \\ w_{N:} \end{array}\right) f \\ =\operatorname{diag}\left(d_{i}\right) f-W f \\ =(D-W) f \\ =L f \end{array} Δf=⎝⎜⎛Δf1⋮ΔfN⎠⎟⎞=⎝⎜⎛d1f1−w1:f⋮dNfN−wN:f⎠⎟⎞=⎝⎜⎛d1⋮0⋯⋱⋯0⋮dN⎠⎟⎞f−⎝⎜⎛w1:⋮wN:⎠⎟⎞f=diag(di)f−Wf=(D−W)f=Lf
这里的 ( D − W ) (D-W) (D−W) 就是拉普拉斯矩阵 L L L 根据前面所述,拉普拉斯矩阵中的第 i i i 行实际上反应 了第 i i i 个节点在对其他所有节点产生扰动时所产生的增益累积。直观上来讲,图拉普拉斯反映了当我们在节点 i i i 上施加一个势,这个势以哪个方向能够多顺畅的流向其他节点。谱域中的拉普拉斯矩阵可以理解为是对图的一种矩阵表示形式。
拉普拉斯矩阵归一化
X i X_{i} Xi 代表节点 i i i 的特征向量
A A A 代表邻接矩阵, A i j A_{i j} Aij 代表节点 i , j i, j i,j 之间的边的权。
D D D 代表图的度的矩阵,是一个对角矩阵 (是邻接矩阵的列和或行和) ,即: D i i = ∑ k = 1 N A i k D_{i i}=\sum_{k=1}^{N} A_{i k} Dii=∑k=1NAik 。
拉普拉斯矩阵归一化主要是以下2种:
-
L rw = D − 1 L L^{\text {rw}}=D^{-1} L Lrw=D−1L ,随机归一化图拉普拉斯算子
-
L sn = D − 1 2 L D − 1 2 L^{\text {sn }}=D^{-\frac{1}{2}} L D^{-\frac{1}{2}} Lsn =D−21LD−21,对称归一化图拉普拉斯算子
-
为何要归一化?
采用加法规则 L = D − A L=D-A L=D−A时,首先在计算节点新的表征只是考虑了邻居节点的信息,没有自己的信息。然后,只是对邻居节点求和,没有平均,这会导致对于度大的节点特征越来越大,而对于度小的节点却相反,这可能导致网络训练过程中梯度爆炸或者消失的问题。因此需要进行归一化。
- 如何归一化?
针对第一个问题,我们可以给图中每个节点增加自连接,实现上可以直接改变邻接矩阵:
A ~ = A + I D ~ = D + I (16) \tilde{A} = A + I\\ \tilde{D} = D + I\tag{16} A~=A+ID~=D+I(16)
然后计算拉普拉斯矩阵:
L s n = D ~ − 1 / 2 A ~ D ~ − 1 / 2 (17) {L}^{sn} = \tilde{D }^{-1/2}\tilde{A}\tilde{D}^{-1/2}\tag{17} Lsn=D~−1/2A~D~−1/2(17)
简单的随机归一化方法: D ~ − 1 A ~ \tilde{D}^{-1}\tilde{A} D~−1A~ 得到的矩阵是非对称阵,所以使用对称归一化的方法: D ~ − 1 / 2 A ~ D ~ − 1 / 2 \tilde{D }^{-1/2}\tilde{A}\tilde{D}^{-1/2} D~−1/2A~D~−1/2
- 举例
假设存在一个 图
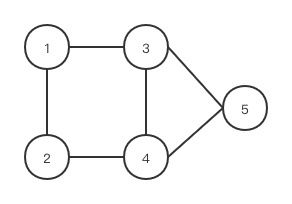
A = [ 0 1 1 0 0 1 0 0 1 0 1 0 0 1 1 0 1 1 0 1 0 0 1 1 0 ] , A ~ = [ 1 1 1 0 0 1 1 0 1 0 1 0 1 1 1 0 1 1 1 1 0 0 1 1 1 ] A = \left[ \begin{matrix} 0 & 1 & 1 & 0 & 0 \\ 1 & 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 & 1 \\ 0 & 1 & 1 & 0 & 1 \\ 0 & 0 & 1 & 1 & 0 \end{matrix} \right] , \tilde{A} = \left[ \begin{matrix} 1 & 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 1 & 0 \\ 1 & 0 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 & 1 \\ 0 & 0 & 1 & 1 & 1 \end{matrix} \right] A=⎣⎢⎢⎢⎢⎡0110010010100110110100110⎦⎥⎥⎥⎥⎤,A~=⎣⎢⎢⎢⎢⎡1110011010101110111100111⎦⎥⎥⎥⎥⎤
D = [ 2 0 0 0 0 0 2 0 0 0 0 0 3 0 0 0 0 0 3 0 0 0 0 0 2 ] , D ~ = [ 3 0 0 0 0 0 3 0 0 0 0 0 4 0 0 0 0 0 4 0 0 0 0 0 3 ] D = \left[ \begin{matrix} 2 & 0 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 & 0 \\ 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 0 & 2 \end{matrix} \right] , \tilde{D} = \left[ \begin{matrix} 3 & 0 & 0 & 0 & 0 \\ 0 & 3 & 0 & 0 & 0 \\ 0 & 0 & 4 & 0 & 0 \\ 0 & 0 & 0 & 4 & 0 \\ 0 & 0 & 0 & 0 & 3 \end{matrix} \right] D=⎣⎢⎢⎢⎢⎡2000002000003000003000002⎦⎥⎥⎥⎥⎤,D~=⎣⎢⎢⎢⎢⎡3000003000004000004000003⎦⎥⎥⎥⎥⎤
D ~ − 1 = [ 1 / 3 0 0 0 0 0 1 / 3 0 0 0 0 0 1 / 4 0 0 0 0 0 1 / 4 0 0 0 0 0 1 / 3 ] \tilde{D}^{-1} = \left[ \begin{matrix} 1/3 & 0 & 0 & 0 & 0 \\ 0 & 1/3 & 0 & 0 & 0 \\ 0 & 0 & 1/4 & 0 & 0 \\ 0 & 0 & 0 & 1/4 & 0 \\ 0 & 0 & 0 & 0 & 1/3 \end{matrix} \right] D~−1=⎣⎢⎢⎢⎢⎡1/3000001/3000001/4000001/4000001/3⎦⎥⎥⎥⎥⎤
则
D ~ − 1 A ~ = [ 1 / 3 1 / 3 1 / 3 0 0 1 / 3 1 / 3 0 0 0 1 / 4 0 1 / 4 1 / 4 1 / 4 0 1 / 4 1 / 4 1 / 4 1 / 4 0 0 1 / 3 1 / 3 1 / 3 ] \tilde{D}^{-1}\tilde{A} = \left[ \begin{matrix} 1/3 & 1/3 & 1/3 & 0 & 0 \\ 1/3 & 1/3 & 0 & 0 & 0 \\ 1/4 & 0 & 1/4 & 1/4 & 1/4 \\ 0 & 1/4 & 1/4 & 1/4 & 1/4 \\ 0 & 0 & 1/3 & 1/3 & 1/3 \end{matrix} \right] D~−1A~=⎣⎢⎢⎢⎢⎡1/31/31/4001/31/301/401/301/41/41/3001/41/41/3001/41/41/3⎦⎥⎥⎥⎥⎤
该矩阵不再是对角阵了,为了保持它是对角阵。所以我们对 A ~ \tilde{A} A~ 左乘 D ~ − 1 / 2 \tilde{D}^{-1 / 2} D~−1/2,右乘 D ^ − 1 / 2 \hat{D}^{-1 / 2} D^−1/2, 得到 D ~ − 1 / 2 A ~ D ~ − 1 / 2 \tilde{D}^{-1 / 2} \tilde{A} \tilde{D}^{-1 / 2} D~−1/2A~D~−1/2 。这样既得到了近似的归一化也保持了矩阵对称性。(左乘是行变换,右乘是列变换。)
随机归一化推导
对 X i X_{i} Xi进行聚合,就是归一化的矩阵与特征向量矩阵 X X X的乘积:
aggregate ( X i ) = ( D ~ − 1 A ~ X ) i = ( D ~ − 1 A ~ ) i x = ( ∑ k = 1 N D ~ i k − 1 A ~ i ) X = ( D ~ i i − 1 A ~ i ) X = D ~ i i − 1 ∑ j = 1 N A ~ i j X j = ∑ j = 1 N 1 D ~ i i A ~ i j X j = ∑ j = 1 N A ~ i j ∑ k = 1 N A ~ i k X j (18) \begin{aligned} \text { aggregate }\left(X_{i}\right)=\left(\tilde{D}^{-1} \tilde{A} X\right)_{i} &=\left(\tilde{D}^{-1} \tilde{A}\right)_{i} x \\ &=\left(\sum_{k=1}^{N}\tilde{D}_{i k}^{-1} \tilde{A}_{i}\right) X \\ &=\left(\tilde{D}_{i i}^{-1} \tilde{A}_{i}\right)X \\ &=\tilde{D}_{i i}^{-1} \sum_{j=1}^{N} \tilde{A}_{i j} X_{j} \\ &=\sum_{j=1}^{N} \frac{1}{\tilde{D}_{i i}} \tilde{A}_{i j} X_{j} \\ &=\sum_{j=1}^{N} \frac{\tilde{A}_{i j}}{\sum_{k=1}^{N} \tilde{A}_{i k}} X_{j} \end{aligned}\tag{18} aggregate (Xi)=(D~−1A~X)i=(D~−1A~)ix=(k=1∑ND~ik−1A~i)X=(D~ii−1A~i)X=D~ii−1j=1∑NA~ijXj=j=1∑ND~ii1A~ijXj=j=1∑N∑k=1NA~ikA~ijXj(18)
这种聚合方式其实是对节点的特征求平均,进行了归一化,权值之和归一化为1,避免求和方式所造成的问题。
对称归一化推导
而 D ~ − 1 / 2 A ~ D ~ − 1 / 2 \tilde{D }^{-1/2}\tilde{A}\tilde{D}^{-1/2} D~−1/2A~D~−1/2 这种归一化方式, 将不再单单地对节点特征取平均, 它不仅考虑了节点 i i i对度, 也考虑了邻接节点 j j j的度, 当邻居节点 j j j度数较大时,它在聚合时贡献会更少。
aggregate ( X i ) = ( D ~ − 0.5 A ~ D ~ − 0.5 X ) i = ( D ~ − 0.5 A ~ ) i D ~ − 0.5 X = ( ∑ k = 1 N D ~ i k − 0.5 A ~ i ) D ~ − 0.5 X = D ~ i i − 0.5 ∑ j = 1 N A ~ i j ∑ k = 1 N D ~ j k − 0.5 X j = D ~ i i − 0.5 ∑ j = 1 N A ~ i j D ~ j j − 0.5 X j = ∑ j = 1 N 1 D ~ i i D ~ j j A ~ i j X j (18) \begin{aligned} \text { aggregate }\left(X_{i}\right)=\left(\tilde{D}^{-0.5} \tilde{A} \tilde{D}^{-0.5} X\right)_{i} &=\left(\tilde{D}^{-0.5} \tilde{A}\right)_{i} \tilde{D}^{-0.5} X \\ &=\left(\sum_{k=1}^{N} \tilde{D}_{i k}^{-0.5} \tilde{A}_{i}\right) \tilde{D}^{-0.5} X\\ &=\tilde{D}_{i i}^{-0.5} \sum_{j=1}^{N} \tilde{A}_{i j} \sum_{k=1}^{N} \tilde{D}_{j k}^{-0.5} X_{j} \\ &=\tilde{D}_{i i}^{-0.5} \sum_{j=1}^{N} \tilde{A}_{i j} \tilde{D}_{j j}^{-0.5} X_{j} \\ &=\sum_{j=1}^{N}\frac{1}{\sqrt{\tilde{D}_{i i} \tilde{D}_{j j}}} \tilde{A}_{i j} X_{j} \end{aligned}\tag{18} aggregate (Xi)=(D~−0.5A~D~−0.5X)i=(D~−0.5A~)iD~−0.5X=(k=1∑ND~ik−0.5A~i)D~−0.5X=D~ii−0.5j=1∑NA~ijk=1∑ND~jk−0.5Xj=D~ii−0.5j=1∑NA~ijD~jj−0.5Xj=j=1∑ND~iiD~jj1A~ijXj(18)
显而易见, 通过 D ~ − 0.5 A ~ D ~ − 0.5 \tilde{D}^{-0.5} \tilde{A} \tilde{D}^{-0.5} D~−0.5A~D~−0.5 操作, 实现了 D ~ i i \tilde{D}_{i i} D~ii 和 D ~ j j \tilde{D}_{j j} D~jj 的几何平均 D ~ j j D ~ j j \sqrt{\tilde{D}_{j j} \tilde{D}_{j j}} D~jjD~jj, 从而考虑了被聚合节点 j j j 的度 D ~ j j \tilde{D}_{j j} D~jj的影响。
学习过程的记录,如有侵权删!请大家多多支持我哦!!!文章可以会不定期的修改和添加内容哦。
参考
拉普拉斯算子和拉普拉斯矩阵,图拉普拉斯算子推导
谱聚类方法推导和对拉普拉斯矩阵的理解
拉普拉斯矩阵归一化
helper.ipam.ucla.edu/publications/dlt2018/dlt2018_14506.pdf