LintCode领扣算法问题答案：1892 · 扫雷

1892 · 扫雷：

现在有一个简易版的扫雷游戏。你将得到一个n*m大小的二维数组作为游戏地图。
每个位置上有一个值（0或1，1代表此处没有雷，0表示有雷）。
你将获得一个起点的位置坐标（x，y），x表示所在行数，y表示所在列数（x，y均从0开始计数）。
若当下位置上没有雷，则上下左右四个方向均可以到达，若当下位置有雷，则不能再往新的方向移动。
返回所有可以到达的坐标。

• 0 < n,m <= 200.
  答案返回一个任意顺序的数组，数组包括所有可以到达的位置坐标。

样例 1

输入: 
	[[1,0,0,0],[1,0,0,0],[0,1,1,1],[0,1,0,0]]
	[0,1]
输出: 
	[[0,1]]
解释：
	[0,1]位置上是0，不能再往新的地方走，只能到达这一个位置

样例 2

输入: 
	[[1,0,0,0],[1,0,0,0],[0,1,1,1],[0,1,0,0]]
	[1,0]
输出: 
	[[0,0],[1,0],[1,1],[2,0],[0,1]]
解释：
	[1,0]位置上是1，所以可以走到[[0,0],[1,1],[2,0]],其中只有[0,0]位置上是1可以继续走到[0,1],然后不能再走了。

原题传送门

---

---

分析

本题无论是深度优先，还是广度优先，都必然有处理重复的问题，已经走过的点是要跳过处理的。

题解

public class Solution {
     
    /**
     * @param Mine_map: an array represents the map.
     * @param Start: the start position.
     * @return: return an array including all reachable positions.
     */
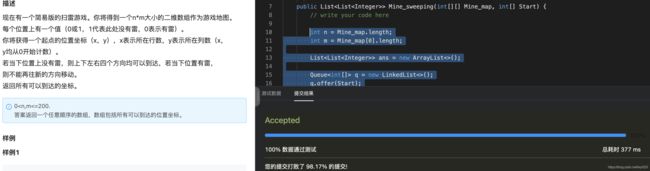
    public List<List<Integer>> Mine_sweeping(int[][] Mine_map, int[] Start) {
     
        // write your code here

        int n = Mine_map.length;
        int m = Mine_map[0].length;

        List<List<Integer>> ans = new ArrayList<>();

        Queue<int[]> q = new LinkedList<>();
        q.offer(Start);
        // 标记已经处理，并且还要能区分原来的值是0还是1
        Mine_map[Start[0]][Start[1]] ^= 2;

        int[][] ds = new int[][]{
     {
     -1, 0}, {
     1, 0}, {
     0, -1}, {
     0, 1}};
        while (!q.isEmpty()) {
     
            int[] p = q.poll();

            List<Integer> row = new ArrayList<>(2);
            row.add(p[0]);
            row.add(p[1]);
            ans.add(row);

            if (Mine_map[p[0]][p[1]] == 3) {
     
                for (int[] d : ds) {
     
                    int[] np = new int[]{
     p[0] + d[0], p[1] + d[1]};
                    if (np[0] >= 0
                            && np[0] < n
                            && np[1] >= 0
                            && np[1] < m
                            && Mine_map[np[0]][np[1]] < 2) {
     
                        q.offer(np);
                        // 标记已经处理，并且还要能区分原来的值是0还是1
                        Mine_map[np[0]][np[1]] ^= 2;
                    }
                }
            }
        }

        return ans;
    }
}

最后说两句

非常感谢你阅读本文章，如果你觉得本文对你有所帮助，请留下你的足迹，点个赞，留个言，多谢~

作者水平有限，如果文章内容有不准确的地方，请指正。

希望小伙伴们都能每天进步一点点。

声明

本文由二当家的白帽子博客原创，转载请注明来源，谢谢~