如何评价Google提出的MLP-Mixer:只需要MLP就可以在ImageNet上达到SOTA?
MLP-Mixer、Beyond Self-attention、RepMLP、Do You Even Need Attention?四篇论文解读点击这里:MLP-Mixer、Beyond Self-attention、RepMLP、Do You Even Need Attention?论文解读以及对MLP的有关评价。
前言
MLP-Mixer: An all-MLP Architecture for Vision是谷歌大脑的研究员(原ViT团队)在网络架构设计方面挖的新坑,它无需卷积、注意力机制,MLP-Mixer仅需MLP即可达到与CNN、Transformer相媲美的性能。比如,在JFT-300M数据集预训练+ImageNet微调后,所提Mixer-H/14取得87.94%的top1精度。
MLP-Mixer这篇论文的创新点和不足
首先我们先简单了解一下,MLP-Mixer这篇论文的创新点和不足:
MLP-Mixer无需卷积与自注意力。相反,MLP-Mixer仅仅依赖于在空域或者特征通道上重复实施的多层感知器,和基础的矩阵乘法操作、数据尺度变换(比如reshape、transposition)以及非线性层。当在大数据集上训练,或者采用先进正则技术训练后,MLP-Mixer在图像分类基准数据集上取得了极具竞争力的性能。
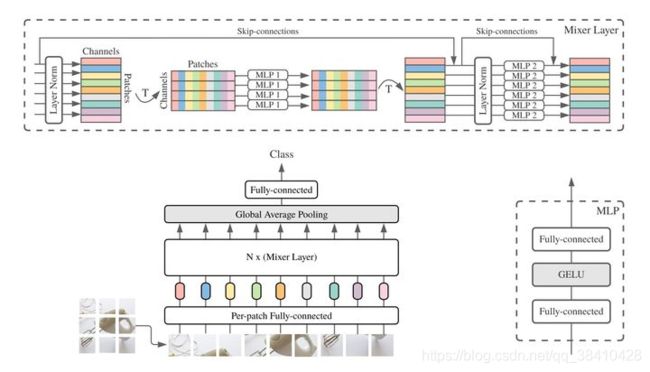
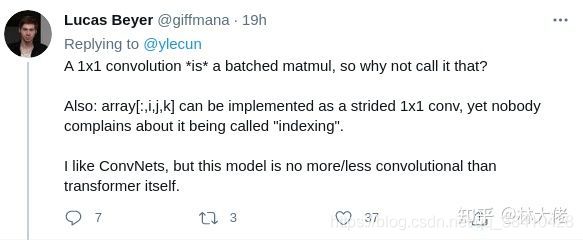
如上图所示是MLP-Mixer的网络结构,它以一系列图像块的线性投影,其形状为(Patches x , Channels)缩写为(S, C)作为输入,其中C是输入数据的通道数,假设原始输入图像分辨率为HW,每个块的分辨率为PP,就那么序列长度S=HW/(P*P)。
MLP-Mixer采用了两种类型的MLP层(注:这两种类型的MLP层交替出现,促进了两个维度间的信息交互):
- Channel-mixing MLP:允许不同通道之间进行通信,每个token独立处理,即采用每一行作为输入。
- token-mixingMLP:允许不同空间位置(token)之间进行通信,每个通道图例处理,即采用每一列作为输入。
重点是:在极端情况下,MLP-Mixer所提架构可视作一种特殊CNN,它采用 [公式] 卷积进行channel mixing,全感受野、参数共享的的单通道深度卷积进行token mixing。
这篇论文也存在着一些不足:
- 结果毕竟没有达到SOTA,只能说可以比较,与ViT还是相差甚远。
- MLP-Mixer也加入了诸如残差结构,LayerNorm这些结构,这其实是最近CNN, Transformer发展的产物,除去这些,效果可能不尽人意。
- Mixer的扩展性没有Transformer强,Transformer的超强扩展性是它横扫CV, NLP等各大任务的原因。而Mixer并没有那么友好的Encoder-Decoder结构,扩展性就没有那么强了。
- Transformer是self attention(SA)和MLP结合的产物,个人觉得SA用于对特征进行选择(判断那些特征重要,那些不重要,关注重要的,忽略不重要的),MLP用于特征的增强。而Mixer虽然在spatial 和channel两个纬度对信息进行了增强,但由于缺少了特征选择的步骤,所以性能上差点意思。
各界人士对这篇论文的评价
接下来让我们看一下各界人士对这篇论文的评价:
特斯拉 AI 高级总监 Andrej Karpathy 认为:「很好!1×1 卷积通常利用深度卷积实现堆叠或交替,但在这里,通道或空间混合得到简化或者实现完全对称。」
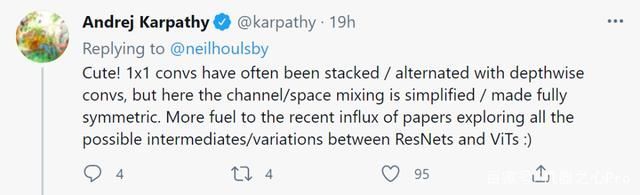
另一用户表示:「CV 领域网络架构的演变从 MLP 到 CNN 到 Transformer 再回到 MLP,真是太有意思了。」
不过,谷歌 DeepMind 首席科学家 Oriol Vinyals 也提出了质疑,他认为:「per-patch 全连接,那不就是卷积吗」

在知乎界,有大佬就直接提出(下面内容来自:LeCun痛斥大热的MLPMixer是挂羊肉卖狗肉?):
这是要回到最初的起点了吗?
要知道,深度学习发展到今天,就是通过简单的MLP -> CNN -> Transformer 一路走过来了,现在谷歌提出不要什么CNN, MLP就可以,可谓是惊呆众人.
也有匿名大佬提出:
最初的MLP之所以搞不起来,是因为参数爆炸,算力不足.现在算力已经不是问题了,是否可以返璞归真了呢?结合算力和数据,啥丹都能练出来.
该答主甚至提出:
如果这个方向正确,之前CNN所有探索出来的结构恐怕都要束之高阁.
不仅令人唏嘘,原来我们花费大量力气优化的模型结构,到头来并非是最优解?这里合理吗?
号称是业内杠把子的Yann LeCun显然是对这篇论文颇有争议,甚至是颇有微词,痛斥大热的MLP-Mixer是挂羊头卖狗肉?
Yann LeCun 表示万物皆可卷积:
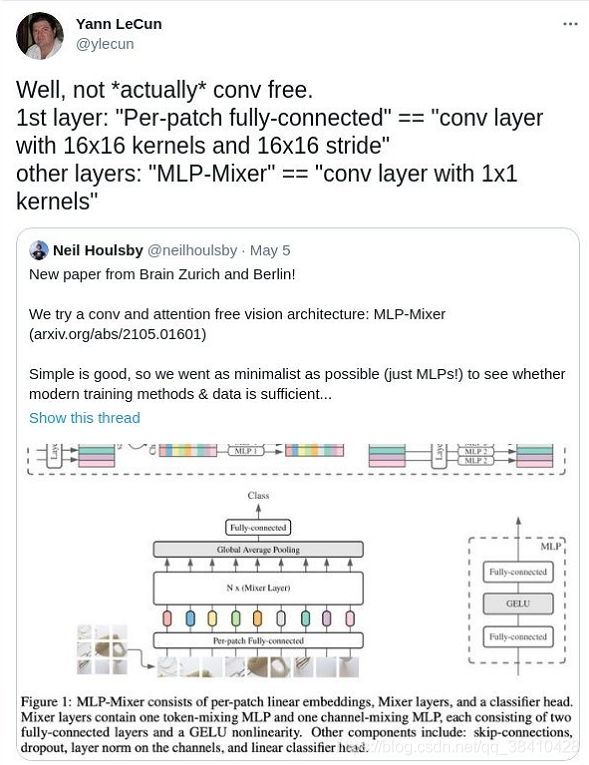
你这哪是ConvFree? 你这分明是一个16x16的步长为16的卷积嘛!任何MLP不就是一个1x1的Conv卷积核吗?
这还没完,楼下的评论就亮了,有人就回复说:
你这么说,那任何1x1的卷积不都是Batched的矩阵乘法吗?那干脆直接叫矩阵乘法不就行了?
好家伙,没想到国外也这么多杠精,但是没关系,杠归杠,我吃瓜群众还是要吃瓜的。这人这么一说,LeCun表示不乐意了:
一个Dense层就是一个1x1的卷积,而且是优化的写法,这个点我老早在1990年代就已经提到了.
也有人说:
这么说来,任何一个向量的乘法,都是一个1x1的卷积?
LeCun老师一针见血的回答道:
不,除非你拿卷积核去乘以输入的每一行,才是卷积.
好家伙,不愧是卷积之父.有人说了:
一个MLP就是一个卷积网络,当你的输入没有步长的时候.
LeCun老师回复:
理论上是这样的,但问题是,输出尺寸固定吗?或者你的输出会随着你的输入增长也增加?如果是,那就是卷积层.
不得不说,卷积之父的推特回答里说的每句话,都值得我们这些菜鸟一般的吃瓜群众好好地思考.颇具哲理。
事情还没有完.LeCun老师甚至说:MLP-Mixer? 这不就是烹饪艺术吗??
用不了多久就会有新的论文出来: Data efficient MLP remixed. 烹饪的艺术.
今天我们的Lecun`老师,再次在推特进行灵魂的拷问:
为毛现在的深度学习架构都叫做: “线性嵌入的16x16非重合贴片,而不是一个16x16的卷积核和16的步长的卷积?”
确实mixer是卷积的一种特殊形式,但是这不妨碍我们叫mixer MLP啊?因为这更好阐述我们的思想和加深大家的理解呀!
Lecun老师直接幽默的回答:
是的,没错.除了它的实现其实就是: x = nn.Conv(self.hidden_dim, (s,s), stride=(s,s))(x)
你说MLP为什么不叫1x1的卷积,尼玛你怎么不说所有的卷积都叫做MLP呢?
这口水战真的越来越有意思了,有点知乎那味儿了!
也有妹子非常实在的答道:
这还不简单,因为你说第二标题你的论文就会被锯掉,因为太直接了。
F.conv2d 实现了 MLP-Mixer
知乎 @Towser用户在文章《MLP-Mixer 里隐藏的卷积》中用 F.conv2d 实现了 MLP-Mixer, 接下来我们详细的看一下他具体的做法:
作为 “an architecture based exclusively on multi-layer perceptrons”,第一步 patch projection 的官方实现就是 Conv,惊不惊喜?意不意外??
嘲讽完毕以后,这里还是要详细解释一下 MLP-Mixer 的几个结构到底和卷积如何对应,不然我写这篇文章也就毫无意义了。
首先,从原则上来说,卷积和全连接层可以按照如下的方式互相转化:
- 如果卷积核的尺寸大到包含了所有输入,以至于无法在输入上滑动,那么卷积就变成了全连接层。
- 反过来,如果全连接层足够稀疏,后一层的每个神经元只跟前一层对应位置附近的少数几个神经元连接,并且这些连接的权重在不同的空间位置都相同,那么全连接层也就变成了卷积层。
一些更具体的例子可以参考 CS231N 这里的解释。
由于第一点关系,你甚至可以说一切层都是卷积层(pytorch 实现就是把输入从 [batch_size, …] reshape 为 [batch_size, -1, 1, 1],然后和一个形如 [out_dim, in_dim, 1, 1] 的卷积核进行 1x1 卷积 ),只是这种说法过于宽泛而缺乏实际意义罢了。作为一个“有意义”的卷积层,至少要满足两个要素:局部连接和参数共享。也就是说,卷积核不要太大,要能够在输入上滑动,这才能体现“卷积”的计算过程。
在 MLP-Mixer 中,主要有三个地方用到了全连接层,而这些操作全部可以用卷积实现,方法如下:
第一步是把输入切分成若干 16x16 的 patch,然后对每个 patch 使用相同的投影。最简单的实现/官方实现就是采用 16x16 的卷积核,然后 stride 也取 16x16,计算二维卷积。当然,这一步也可以按照全连接层来实现:首先把每个 16x16 的 patch 中的像素通过 permute/reshape 等操作放在最后一维得到 x_mlp,然后再做一层线性变换。
为了方便参数共享、对比计算结果,这里全部采用 pytorch 里的 functional API 实现,代码如下:
import torch
import torch.nn.functional as F
# i) non-overlapping patch projection
batch_size, height, width, in_channels = 32, 224, 224, 3
out_channels, patch_size = 8, 16
x = torch.randn(batch_size, in_channels, height, width)
w1 = torch.randn(out_channels, in_channels, patch_size, patch_size)
b1 = torch.randn(out_channels)
conv_out1 = F.conv2d(x, w1, b1, stride=(patch_size, patch_size))
print(conv_out1.size()) # [batch_size, out_channels, num_patches_per_column, num_patches_per_row]
x_mlp = x.view(batch_size, in_channels, height // patch_size, patch_size, width // patch_size, patch_size).\
permute(0, 2, 4, 1, 3, 5).reshape(batch_size, -1, in_channels * patch_size ** 2)
mlp_out1 = x_mlp @ w1.view(out_channels, -1).T + b1
print(mlp_out1.size()) # [batch_size, num_patches, out_channels]
print(torch.allclose(conv_out1.view(-1), mlp_out1.transpose(1, 2).reshape(-1), atol=1e-4))
可以看到,在对结果进行重新排列后(这一步繁琐但是意义不大,不展开讲了),conv_out1 和 mlp_out1 是相同的。
torch.Size([32, 8, 14, 14])
torch.Size([32, 196, 8])
True
另一个操作是对同一通道内不同位置的像素信息进行整合。如果用 MLP 来实现,就是把同一个通道的像素值都放到最后一维,然后接一个线性变换即可;如果用卷积来实现,实质上是一个 depthwise conv,并且各个通道/深度要共享参数(因为每个通道都要按相同的方式整合不同位置的信息)。这就是 F.conv2d 的卷积核里 w2 和 b2 进行 repeat 的原因。
# ii) cross-location/token-mixing step
in_channels = out_channels # Use previous outputs as current inputs
out_hidden_dim = 7 # `C` in the paper
x = torch.randn(batch_size, in_channels, height // patch_size, width // patch_size)
w2 = torch.randn(out_hidden_dim, 1, height // patch_size, width // patch_size)
b2 = torch.randn(out_hidden_dim)
# This is a depthwise conv with shared parameters
conv_out2 = F.conv2d(x, w2.repeat(in_channels, 1, 1, 1),
b2.repeat(in_channels), groups=in_channels)
print(conv_out2.size()) # [batch_size, in_channels * out_hidden_dim, 1, 1]
mlp_out2 = x.view(batch_size, in_channels, -1) @ w2.view(out_hidden_dim, -1).T + b2
print(mlp_out2.size()) # [batch_size, in_channels, out_hidden_dim], or [B, S, C] in the paper
print(torch.allclose(conv_out2.view(-1), mlp_out2.view(-1), atol=1e-4))
conv_out2 和 mlp_out2 的结果当然也是相同的(在进行适当重排的意义下):
torch.Size([32, 56, 1, 1])
torch.Size([32, 8, 7])
True
还有一个操作是对同一位置的不同通道进行融合。显然这个操作就是一个逐点卷积(pointwise/1x1 conv)。当然,也可以利用 permute 把相同位置不同通道的元素丢到最后一维去,然后统一做一个线性变换,如下:
# iii) channel-mixing step
out_channels = 28
x = torch.randn(batch_size, in_channels, height // patch_size, width // patch_size)
w3 = torch.randn(out_channels, in_channels, 1, 1)
b3 = torch.randn(out_channels)
# This is a pointwise conv
conv_out3 = F.conv2d(x, w3, b3)
print(conv_out3.size()) # [batch_size, out_channels, num_patches_per_column, num_patches_per_row]
mlp_out3 = x.permute(0, 2, 3, 1).reshape(-1, in_channels) @ w3.view(out_channels, -1).T + b3
print(mlp_out3.size()) # [batch_size * num_patches, out_channels], or [B*C, S] in the paper
print(torch.allclose(conv_out3.permute(0, 2, 3, 1).reshape(-1), mlp_out3.view(-1), atol=1e-4))
结果也是毫无悬念的相同:
torch.Size([32, 28, 14, 14])
torch.Size([6272, 28])
True
大功告成!现在我们已经学会如何用 F.conv2d 实现 MLP-Mixer 了!
当 MLP-Mixer 对每个 patch 做相同的线性变换的时候,就已经在用卷积了(这一点在 ViT 里同样成立)。因为卷积的本质是局部连接+参数共享,而划分 patch = 局部连接,对各个 patch 应用相同的线性变换 = 参数共享。只不过,它用的卷积核大一点儿而已,有一个 patch 那么大。
而当他进行 token-mixing 和 channel mixing 的时候,实际就是把普通的卷积拆成了 depthwise conv with shared parameters 和 pointwise conv —— 在不考虑卷积核大小的情况下,这甚至比深度可分离卷积(depthwise separable conv)的表达能力还要弱:后者是把普通 conv 拆成了 depthwise conv + pointwise conv,而 MLP-Mixer 里的 depthwise conv 甚至还要在每个 depth/channel 上共享参数。于是,达不到 SOTA 也很好理解了。
写到这里,其实也就把 @Captain Jack的一句话评价parameter-shared depth-wise separable convolution掰开讲了。
当然,无意否认这篇文章的贡献,能把这么大的 patch/conv kernel 训出来绝不是一件容易的事情,只是我实在厌倦了 XXX is all you need. Indeed, money is all you need.
题外话:在 Transformer 中,有一个逐点前馈/全连接(pointwise feedforward)的操作,具体内容是给每个位置施加一个相同的前馈变换。有人称之为 1D 卷积,我认为也是合理的,因为它也体现了卷积核滑动的过程。其实,对一个形如 [B, T, D] 的张量做线性变换,得到一个形如 [B, T, D’] 的张量,不要把 D 和 D’ 理解为隐层维度而是理解为通道数,很容易看出这是一个 conv1d。如果在写代码的时候想着用循环实现每个样本每个时间步如何操作,才会觉得 D -> D’ 是一个全连接层(所以它叫逐点全连接:从单点的角度来看,它是全连接;从整个序列输入的角度来看,它是 conv1d)。
补充与MLP相关的论文:
5月4日,谷歌团队在arXiv上提交了一篇论文《MLP-Mixer: An all-MLP Architecture for Vision》。
5月5日,清华大学图形学实验室Jittor团队在arXiv上也提交了一篇和MLP相关的论文《Beyond Self-attention: External Attention using Two Linear Layers for Visual Tasks》。这篇论文提出了一种新的注意力机制,称之为External Attention——基于两个外部的、小的、可学习的和共享的存储器,只用两个级联的线性层和归一化层就可以取代了现有流行的学习架构中的“Self-attention”,进一步揭示了线性层和注意力机制之间的关系。
5月5日,清华大学软件学院丁贵广团队在arXiv上也提交了论文《RepMLP: Re-parameterizing Convolutions into Fully-connected Layers for Image Recognition》。这篇论文展示了结合重参数化技术的MLP也能取得非常不错视觉的效果。
5月6日,牛津大学的学者提交了一篇名为《Do You Even Need Attention? A Stack of Feed-Forward Layers Does Surprisingly Well on ImageNet》的论文,也提出了Transformer中的attention是不必要的,仅仅使用Feed forward就可以在ImageNet上实现非常高的结果。
参考文献
- LeCun痛斥大热的MLPMixer是挂羊肉卖狗肉? https://zhuanlan.zhihu.com/p/370659681
- MLP回归无需卷积、自注意力,纯多层感知机视觉架构媲美CNN、ViT https://baijiahao.baidu.com/s?id=1698992972535694806&wfr=spider&for=pc
- MLP-Mixer 里隐藏的卷积 https://zhuanlan.zhihu.com/p/370774186