matlab入门——矩阵运算
matlab入门——矩阵运算
原创不易,路过的各位大佬请点个赞
矩阵运算
- matlab入门——矩阵运算
-
- 1、矩阵加法
- 2、矩阵减法
- 3、矩阵乘法
-
- 3.1、 数乘运算
- 3.2、 矩阵相乘
- 3.2、点乘运算
- 4、矩阵除法
-
- 4.1、左除法
- 4.2、右除法
- 5、矩阵其它运算汇总
- 6、矩阵幂函数
- 6、矩阵求逆
- 7、矩阵范数、两个点之间的欧几里德距离
-
- 两个点之间的欧几里德距离
矩阵的基本运算包括加、减、乘、数乘、点乘、乘方、左除、右除、求逆等。其中加、减、乘与大家所学的线性代数中的定义是一样的,相应的运算符为“ + + +”、“ − - −”、“ ∗ * ∗”。
矩阵的除法运算是MATLAB所特有的,分为左除和右除,相应运算符为“\”和“ / / /”。一般情况下,方程 A ∗ X = B A*X=B A∗X=B的解是 X = A X=A X=A\ B B B,而方程 X ∗ A = B X*A=B X∗A=B的解是 X = B / A X=B/A X=B/A。
1、矩阵加法
设矩阵 A = a i j A=a_{ij} A=aij, B = b i j B=b_{ij} B=bij都是 m × n m\times n m×n的矩阵,则矩阵 A A A与 B B B的和为
A + B = [ a 11 + b 11 a 12 + b 12 ⋯ a 1 n + b 1 n a 21 + b 21 a 22 + b 22 ⋯ a 2 n + b 2 n ⋮ ⋮ ⋮ ⋮ a m 1 + b m 1 a m 2 + b m 2 ⋯ a m n + b m n ] A+B=\begin{bmatrix} a_{11}+b_{11}&a_{12}+b_{12}&\cdots &a_{1n}+b_{1n} \\ a_{21}+b_{21}&a_{22}+b_{22}&\cdots &a_{2n}+b_{2n}\\ \vdots &\vdots &\vdots &\vdots\\ a_{m1}+b_{m1}&a_{m2}+b_{m2}&\cdots &a_{mn}+b_{mn} \end{bmatrix} A+B=⎣⎢⎢⎢⎡a11+b11a21+b21⋮am1+bm1a12+b12a22+b22⋮am2+bm2⋯⋯⋮⋯a1n+b1na2n+b2n⋮amn+bmn⎦⎥⎥⎥⎤
1. 矩阵交换律: A + B = B + A A+B=B+A A+B=B+A
2. 矩阵j结合律: ( A + B ) + C = A + ( B + C ) (A+B)+C=A+(B+C) (A+B)+C=A+(B+C)
A=[5,6,9,8;5,3,6,7]
B=[3,6,7,9;5,8,9,6]
C=[9,3,5,6;8,5,2,1]
D=[1,5,6;2,5,6]
A+B
B+A
(A+B)+C
A+(B+C)
A+D
2、矩阵减法
计算矩阵 A − B = A + ( − B ) A-B=A+(-B) A−B=A+(−B)
B=[3,6,7,9;5,8,9,6];
A=[5,6,9,8;5,3,6,7];
-B
ans =
-3 -6 -7 -9
-5 -8 -9 -6
A-B
ans =
2 0 2 -1
0 -5 -3 1
3、矩阵乘法
3.1、 数乘运算
>> A=[5,6,9,8;5,3,6,7];
>> A*10
ans =
50 60 90 80
50 30 60 70
3.2、 矩阵相乘
C = A ∗ B C=A*B C=A∗B满足下面条件:
矩阵A的行数与矩阵B的列数相同;
矩阵C的行数等于矩阵A的行数,矩阵C的列数等于矩阵B的列数;
矩阵C的第m行n列元素值等于矩阵A的m行元素与矩阵B的n行元素对应值积的和。
A B ≠ B A AB\neq BA AB=BA,矩阵不满足交换律
[ a 1 a 2 ⋮ a n ] [ a 1 a 2 ⋯ a n ] = [ a 1 b 1 a 1 b 2 ⋯ a 1 b n a 2 b 1 a 2 b 2 ⋯ a 2 b n ⋮ ⋮ ⋮ ⋮ a n b 1 a n b 2 ⋯ a n b n ] \begin{bmatrix} a_{1}\\a_{2}\\\vdots \\a_n \end{bmatrix}\begin{bmatrix} a_{1}&a_{2}&\cdots &a_n \end{bmatrix}= \begin{bmatrix} a_1b_1&a_1b_2&\cdots &a_1b_n \\ a_2b_1&a_2b_2&\cdots &a_2b_n\\ \vdots &\vdots &\vdots &\vdots\\ a_nb_1&a_nb_2&\cdots &a_nb_n \end{bmatrix} ⎣⎢⎢⎢⎡a1a2⋮an⎦⎥⎥⎥⎤[a1a2⋯an]=⎣⎢⎢⎢⎡a1b1a2b1⋮anb1a1b2a2b2⋮anb2⋯⋯⋮⋯a1bna2bn⋮anbn⎦⎥⎥⎥⎤
[ a 1 a 2 ⋯ a n ] ∗ [ a 1 a 2 ⋮ a n ] = a 1 b 1 + a 2 b 1 + ⋯ + a n b n \begin{bmatrix} a_{1}&a_{2}&\cdots &a_n \end{bmatrix}*\begin{bmatrix} a_{1}\\a_{2}\\\vdots \\a_n \end{bmatrix}= a_1b_1+a_2b_1+\cdots+ a_nb_n [a1a2⋯an]∗⎣⎢⎢⎢⎡a1a2⋮an⎦⎥⎥⎥⎤=a1b1+a2b1+⋯+anbn
3.2、点乘运算
点乘运算指将两矩阵中相同位置的元素进行相乘运算,将积保存在原位置组成新矩阵。
B=[3,6,7,9;5,8,9,6];
A=[5,6,9,8;5,3,6,7];
A.*B
ans =
15 36 63 72
25 24 54 42
>> A=[0 0;1 1]
B=[1 0;2 0]
6*A - 5*B
A*B-A
B*A-A
A.*B-A
A*B./A-A
A =
0 0
1 1
B =
1 0
2 0
ans =
-5 0
-4 6
ans =
0 0
2 -1
ans =
0 0
-1 -1
ans =
0 0
1 -1
ans =
NaN NaN
2 -1
4、矩阵除法
计算左除A\B时,A的行数要与B的行数一致,计算右除A/B时,A的列数要与B的列数致。
4.1、左除法
线性方程组 D ∗ X = B D*X=B D∗X=B,如果 D D D非奇异,即它的逆矩阵 inv ( D ) \text{inv}(D) inv(D)存在,则其解用MATLAB表示为
X − inv ( D ) ∗ B = D 右 除 B X-\text{inv}(D)*B=D右除B X−inv(D)∗B=D右除B
符号“\”称为左除,即分母放在左边。
左除的条件:B的行数等于D的阶数(D的行数和列数相同,简称阶数)。
A=[1 2 3;5 8 6];
B=[8 6 9;4 3 7];
C=A./B
D=B.*C
C =
0.1250 0.3333 0.3333
1.2500 2.6667 0.8571
D =
1 2 3
5 8 6
4.2、右除法
线性方程组 X ∗ D = B X*D=B X∗D=B,如果 D D D非奇异,即它的逆矩阵 inv ( D ) \text{inv}(D) inv(D)存在,则其解用MATLAB表示为
X = B ∗ inv ( D ) = B / D X=B*\text{inv}(D)=B/D X=B∗inv(D)=B/D
符号“/”称为左除,即分母放在右边。
右除的条件:B的列数等于D的阶数(D的行数和列数相同,简称阶数)。
A=[1 2 3;5 8 6];
B=[8 6 9;4 3 7];
A.\B
A./B
ans =
8.0000 3.0000 3.0000
0.8000 0.3750 1.1667
ans =
0.1250 0.3333 0.3333
1.2500 2.6667 0.8571
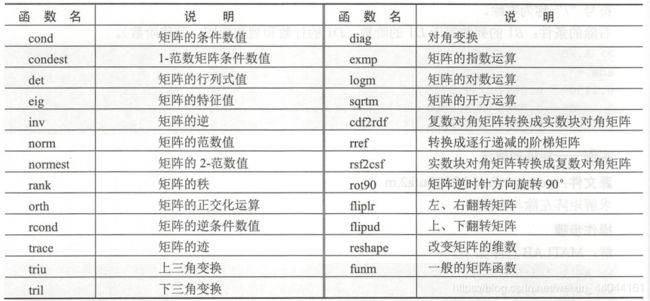
5、矩阵其它运算汇总
6、矩阵幂函数
A A A阶方阵,其 k k k次幂为
A k = A A A A A A A A^k=AAAAAAA Ak=AAAAAAA
A=[1,2,3;4,5,6;2,3,4];
A.^2
A^2
ans =
15 21 27
36 51 66
22 31 40
( A ∗ B ) k ≠ A k ∗ B k (A*B)^k\neq A^k*B^k (A∗B)k=Ak∗Bk
A=[1 2 3;0 3 3;7 9 5];
B=[5,6,8;6,0,5;4,5,6];
(A*B)^5
A^5*B^5
ans =
1.0e+11 *
0.3047 0.1891 0.3649
0.2785 0.1728 0.3335
1.0999 0.6825 1.3173
ans =
1.0e+10 *
2.5561 2.1096 3.3613
2.5561 2.1095 3.3613
6.8284 5.6354 8.9793
6、矩阵求逆
对于 n n n阶方阵 A A A,如果有 n n n阶方阵 B B B满足 A B = B A = I AB=BA=I AB=BA=I,则称矩阵A为可逆的,称方阵 B B B为 A A A的逆矩阵,记为 A − 1 A^{-1} A−1。
逆矩阵的基本性质:
- 若 A A A可逆,则 A − 1 A^{-1} A−1是唯一的。
- 若 A A A可逆,则 A − 1 A^{-1} A−1也可逆,并且 ( A − 1 ) − 1 = A (A^{-1})^{-1}=A (A−1)−1=A。
- 若 n n n阶方阵 A A A与 B B B都可逆,则 A B AB AB也可逆,且 ( A B ) − 1 (AB)^{-1} (AB)−1= B − 1 A − 1 B^{-1}A^{-1} B−1A−1。
- 若 A A A可逆,则 ∣ A − 1 ∣ = ∣ A ∣ − 1 |A^{-1}|=|A|^{-1} ∣A−1∣=∣A∣−1。
我们把满足 A ≠ 0 A\neq0 A=0的方阵 A A A称为非奇异的,否则就称为奇异的。求解矩阵的逆使用函数inv,调用格式如下。
Y = inv ( X ) Y=\text{inv}(X) Y=inv(X)
A=rand(3)
B = inv(A)
A =
0.9575 0.9706 0.8003
0.9649 0.9572 0.1419
0.1576 0.4854 0.4218
B =
1.6626 -0.1039 -3.1198
-1.9097 1.3790 3.1597
1.5764 -1.5481 -0.0994
7、矩阵范数、两个点之间的欧几里德距离
范数是数值分析中的一个概念,它是向量或矩阵大小的一种度量,在工程计算中有着重要的作用。对于向量 x ∈ R n x\in\mathbb{R}^n x∈Rn,常用的向量范数有以下几种。

语法:
n = norm(v)
n = norm(v,p)
n = norm(X)
n = norm(X,p)
n = norm(X,‘fro’)
n = norm(v) 返回向量 v 的欧几里德范数。此范数也称为 2-范数、向量模或欧几里德长度。
n = norm(v,p) 返回广义向量 p-范数。
n = norm(X) 返回矩阵 X 的 2-范数或最大奇异值,该值近似于 max(svd(X))。
n = norm(X,p) 返回矩阵 X 的 p-范数,其中 p 为 1、2 或 Inf:
如果 p = 1,则 n 是矩阵的最大绝对列之和,即1范数。
如果 p = 2,则 n 近似于 max(svd(X))。这与 norm(X) 等效,即2范数。
如果 p = Inf,则 n 是矩阵的最大绝对行之和。
如果 p = Inf,则 n 是矩阵的最大绝对行之和。
n = norm(X,‘fro’) 返回矩阵 X 的 Frobenius 范数。
v = [1 -2 3];
n = norm(v)
n = 3.7417
X = [-2 3 -1];
n = norm(X,1)
n = 6
两个点之间的欧几里德距离
a = [0 3];
b = [-2 1];
使用 norm 来计算点之间的距离。
d = norm(b-a)
d = 2.8284