CCF-CSP 202012-2 期末预测之最佳阈值 (Python)

题目背景

考虑到安全指数是一个较大范围内的整数、小菜很可能搞不清楚自己是否真的安全，顿顿决定设置一个阈值 $\theta$，以便将安全指数 $y$ 转化为一个具体的预测结果——“会挂科”或“不会挂科”。
因为安全指数越高表明小菜同学挂科的可能性越低，所以当 $y\ge \theta$ 时，顿顿会预测小菜这学期很安全、不会挂科；反之若 $y<\theta$，顿顿就会劝诫小菜：“你期末要挂科了，勿谓言之不预也。”
那么这个阈值该如何设定呢？顿顿准备从过往中寻找答案。

题目描述

具体来说，顿顿评估了 $m$ 位同学上学期的安全指数，其中第 $i$（$1\le i\le m$）位同学的安全指数为 $y_i$，是一个 $[0,10^8]$ 范围内的整数；同时，该同学上学期的挂科情况记作 $resul{t}_i\in 0,1$，其中 $0$ 表示挂科、$1$ 表示未挂科。
相应地，顿顿用 $predic{t}_{\theta }(y)$ 表示根据阈值 $\theta$ 将安全指数 $y$ 转化为的具体预测结果。
如果 $predic{t}_{\theta }(y_j)$ 与 $resul{t}_j$ 相同，则说明阈值为 $\theta$ 时顿顿对第 $j$ 位同学是否挂科预测正确；不同则说明预测错误。

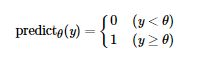
最后，顿顿设计了如下公式来计算最佳阈值 ${\theta }^{\ast }$：

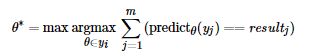
该公式亦可等价地表述为如下规则：

1. 最佳阈值仅在 $y_i$ 中选取，即与某位同学的安全指数相同；
2. 按照该阈值对这 $m$ 位同学上学期的挂科情况进行预测，预测正确的次数最多（即准确率最高）；
3. 多个阈值均可以达到最高准确率时，选取其中最大的。

输入格式

从标准输入读入数据。
输入的第一行包含一个正整数 $m$。
接下来输入 $m$ 行，其中第 $i$（$1\le i\le m$）行包括用空格分隔的两个整数 $y_i$ 和 $resul{t}_i$，含义如上文所述。

输出格式

输出到标准输出。
输出一个整数，表示最佳阈值 ${\theta }^{\ast }$。

样例1输入

6
0 0
1 0
1 1
3 1
5 1
7 1

样例1输出

3

样例1解释

按照规则一，最佳阈值的选取范围为 $0,1,3,5,7$。
$\theta =0$ 时，预测正确次数为 $4$；
$\theta =1$ 时，预测正确次数为 $5$；
$\theta =3$ 时，预测正确次数为 $5$；
$\theta =5$ 时，预测正确次数为 $4$；
$\theta =7$ 时，预测正确次数为 $3$。
阈值选取为 $1$ 或 $3$ 时，预测准确率最高；
所以按照规则二，最佳阈值的选取范围缩小为 $1,3$。
依规则三，${\theta }^{\ast }=\max 1,3=3$。

样例2输入

8
5 1
5 0
5 0
2 1
3 0
4 0
100000000 1
1 0

样例2输出

100000000

子任务

$70\%$ 的测试数据保证 $m\le 200$；
全部的测试数据保证 $2\le m\le 10^5$。

解法

若暴力使用两层for循环会超时，只能拿70分，这里采用前缀和的思想。

m = int(input())
yr = []
# 全部挂科情况的和
sum_r = 0
for i in range(m):
    y, r = list(map(int, input().split()))
    yr.append([y, r])
    sum_r += r
yr = sorted(yr)     # 按安全指数进行从小到大排序
# 存储当前安全指数前面不挂科的和（即对当前安全指数前面的挂科情况求和）
sum = [0]
# 最高准确率
max_acc = sum_r
# 最佳阈值
optimum_yuzhi = yr[0][0]
# 上一个阈值
last_yuzhi = yr[0][0]
for idx, [y, r] in enumerate(yr):
    if idx == 0:
        continue
    sum.append(yr[idx - 1][1] + sum[idx - 1])
    # 当阈值不一样才会去计算当前阈值的准确率
    if y > last_yuzhi:
        last_yuzhi = y
        acc = (idx - sum[idx]) + (sum_r - sum[idx]) # 阈值前0的个数 + 阈值后（包括该阈值）1的个数
        if acc >= max_acc:
            optimum_yuzhi = y
            max_acc = acc
print(optimum_yuzhi)