第十二届蓝桥杯省赛C_C++ 大学 B 组【第一场部分题解】

参加的第一场,做题的时候懵逼了，这不是暴力杯么？咋题怎么不暴力了。
有好几个题目看错了，送了不少分。

试题 A: 空间

答案: 67108864

#include
#include
using namespace std;
int main(void)
{
     
	cout<<256*1024*1024/4<<endl;
	return 0;
}

试题 B: 卡片

答案:3181

#include
#include
using namespace std;
int sum[15];
int main(void)
{
     
	for(int i=0;i<=9;i++) sum[i]=2021;
	int n=1;
	while(n)
	{
     
		int temp=n;
		while(temp)
		{
     
			sum[temp%10]--;
			if(sum[temp%10]<0){
     
				
				cout<<n-1<<endl;//问的是最大可以拼到的数 
				return 0;
			} 
			temp/=10;
		}
		n++;
	}
	return 0;
}

试题 C: 直线 【数学】

首先：你要知道判断一条直线只需枚举所有的任意两点，求斜率和截距就可以了。
但是去重的时候要知道，斜率和截距不一定是整数，故需要排序判断去重。
答案:40257

#include
#include
#include
#include
#include
#include
#include
using namespace std;
vector<pair<double,double>> ve;
int main(void)
{
     
	for(int i=0;i<20;i++)//x1
	{
     
		for(int j=0;j<21;j++)//y1
		{
     
			for(int k=0;k<20;k++)//x2
			{
     
				for(int z=0;z<21;z++)//y2
				{
     
					int x1=i,y1=j,x2=k,y2=z;
					if((x2-x1)!=0)
					{
     
						double  a=(double)(y2-y1)/(x2-x1);
						double  b=(double)y1-a*x1;
						ve.push_back({
     a,b});
					}
				}
			}
		} 
	}
	int ans=1;
	sort(ve.begin(),ve.end());
	for(int i=1;i<ve.size();i++)
	{
     
		if(fabs(ve[i].first-ve[i-1].first)>1e-8||fabs(ve[i].second-ve[i-1].second)>1e-8)
		ans++;
	}
	cout<<ans+20<<endl;//加上的20是 y=0,y=1...y=19 这二十种情况 
	return 0;
}

试题 D: 货物摆放 【数学 / 分解因子】

答案:2430
思路：分解因子后，挨个枚举判断

#include 
#include
#include
using namespace std;
long long int n=2021041820210418;
vector<long long int >ve;
long long int res;
int main(void)
{
     
	for(int i=1;i<=n/i;i++)//分解因子 
	{
     
		if(n%i==0)
		{
     
			ve.push_back(i);
			if(n/i!=i) ve.push_back(n/i);
		}
	}
	for(int i=0;i<ve.size();i++)
	{
     
		for(int j=0;j<ve.size();j++)
		{
     
			for(int k=0;k<ve.size();k++)
			{
     
				if(ve[i]*ve[j]*ve[k]==n) res++;
			}
		}
	}
	cout<<res<<endl;
	return 0;
} 

试题 E: 路径 【最短路 / Dijkstra】

答案：10266837

#include
#include
#include
#include
using namespace std;
const int N=2030;
long long int dist[N];
long long int g[N][N];
bool st[N];
int n,m;
int gcd(int a,int b)
{
     
	if(b==0) return a;
	else return gcd(b,a%b);
}
long long int Dijkstra()
{
     
	memset(dist,0x3f,sizeof dist);
	dist[1]=0;
	
	for(int i=0;i<n;i++)
	{
     
		int t=-1;
		for(int j=1;j<=n;j++)
		if(!st[j]&&(t==-1 || dist[j]<dist[t])) t=j;
		
		for(int j=1;j<=n;j++)
		{
     
			dist[j]=min(dist[j],dist[t]+g[t][j]);
		}
		
		st[t]=true;
	}
	if(dist[n]==0x3f3f3f3f3f3f3f3f) return -1;
	else return dist[n];
}
int main(void)
{
     
	n=2021;
	memset(g,0x3f,sizeof g);
	for(int i=1;i<=2021;i++)
	{
     
		for(int j=i+1;(j<=i+21)&&j<=2021;j++)
		{
     
			long long int x=i*j/gcd(i,j);
			if(g[i][j]>x) g[i][j]=g[j][i]=x;
		}
	}
	cout<<Dijkstra()<<endl; 
	return 0;
} 

试题 F: 时间显示

#include
#include
using namespace std;
long long int t;
int main(void)
{
     
    cin>>t;
    t/=1000;
    printf("%02ld:%02ld:%02ld",(t%(3600*24))/3600,(t%3600)/60,t%60);
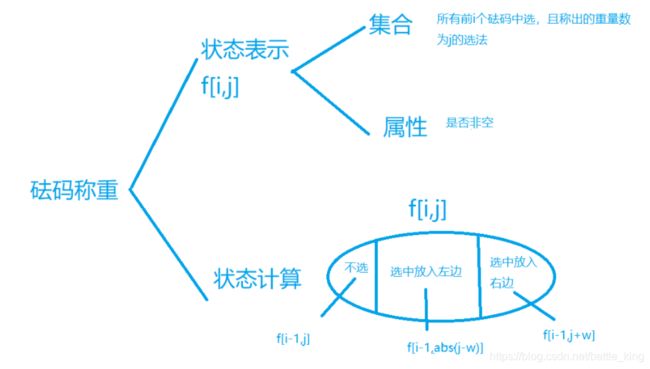
    return 0;
}

试题 G: 砝码称重【DP】

看数据范围推测是一个DP，当然你也可以打暴力，暴力可以过掉一半的分数。
DP分析:
DP的状态表示：f[i][j] 表示选i个砝码可不可以凑出j的体重

首先不难分析出这是一个镜像对称的即，左边放一个 2，3 右边放一个 1 和左边放一个 1 右边放一个 2，3。
这两者测出来的数是一模一样的。
我们假设放左边为 加上 w 放右边为减去 w.
故状态转移方程为: f[i][j]=f[i-1][j] | f[i-1][j-w[i]] | f[i-1][j+w[i]]
因为数组不能有负数故我们统一的加一个偏移量，故总的代码如下:

#include
#include
#include
using namespace std;
const int N=1e5*2+10;
const int B=N/2;
bool f[105][N];
int w[105];
int n;
int main(void)
{
     
	int m=0;
	cin>>n;
	for(int i=1;i<=n;i++) cin>>w[i],m+=w[i];
	f[0][B]=true;
	for(int i=1;i<=n;i++)
	{
     
		for(int j=-m;j<=m;j++)
		{
     
			f[i][j+B]=f[i-1][j+B];
			if(j-w[i]>=-m) f[i][j+B]|=f[i-1][j-w[i]+B];
			if(j+w[i]<=m)  f[i][j+B]|=f[i-1][j+w[i]+B];
		}
	}
	int ans=0;
	for(int i=1;i<=m;i++) if(f[n][i+B]) ans++; // 统计可以凑出来的数量
	cout<<ans<<endl;
	return 0;
}

附上一个大佬画的图。
大佬题解链接

试题 H: 杨辉三角形 【组合数 / 规律】

首先你要知道杨辉三角的一个特点就是它的每一个数都是一个组合数。如上图所示。
由上图对称故：我们只需讨论一半就可以了。

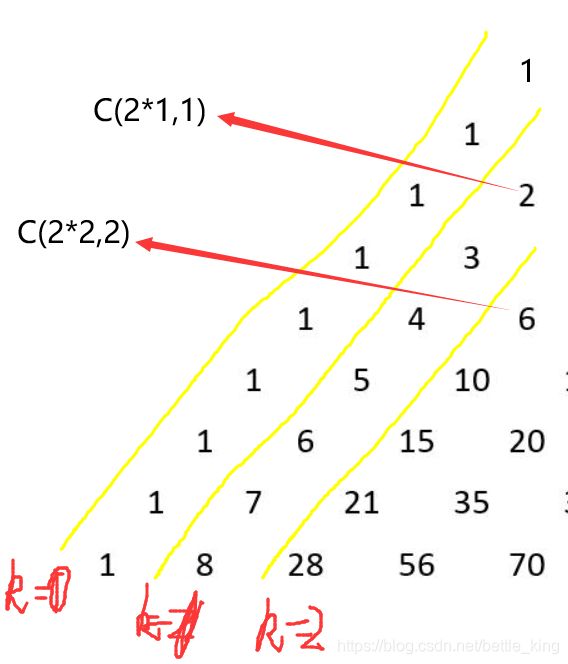
我们斜着一行一行的看，可以看到斜着一行是递增的最小的是 C(2xk,k)
因为C(34,17)>1e9 故我们只需枚举k=16 到 0 就可以了。
注意是从内到外枚举，这样找的才是第一次出现的，不懂的看图分析一下就好了。

#include
#include
#include
using namespace std;
typedef long long int LL;
int n;
LL C(int a,int b)
{
     
    LL res=1;
    for(int i=a,j=1;j<=b;j++,i--)
    {
     
        res=res*i/j;
        if(res>n) return res;
    }
    return res;
}
bool check(int k)
{
     
    int l=k*2,r=n;
    while(l<r)
    {
     
        int mid=l+r>>1;
        if(C(mid,k)>=n) r=mid;
        else l=mid+1;
    }
    if(C(l,k)==n)
    {
     
        cout<<(LL)r*(r+1)/2+k+1<<endl;  //是从0开始的故需加1
        return true;
    }
    return false;
}
int main(void)
{
     
    cin>>n;
    for(int k=16;k>=0;k--)
    {
     
        if(check(k)) break;
    }
    return 0;
}