机器学习笔记6 -- 隐马尔科夫模型 Hidden Markov Model
Table of Contents
问题域
为什么HMM可以解决NLP问题
HMM基于两个假设
模型训练
三组参数
三个基本问题
问题域
概率模型将学习任务归结于计算变量的概率分布,其核心是如何基于可观测变量推测出未知变量的条件分布。
概率图模型就是一类用图来表达变量相关关系的概率模型,根据性质不同可以分为两类:第一类是使用有向无环图表示变量之间的依赖关系,称为有向图模型或者贝叶斯网;第二类是使用无向图表示变量间的相关关系,称为无向图模型或者马尔科夫网。隐马尔科夫模型是结构最简单的动态贝叶斯网,主要用于时序数据建模,是解决大多数自然语言处理问题最为快速、有效的方法。它成功的解决了复杂的语音识别、机器翻译等问题。
为什么HMM可以解决NLP问题
自然语言是人类交流信息等工具,语言和通信有天然的联系。但在自然语言处理研究早期,努力都集中在语法语义上,离通信等原理越来越远,当研究方向回归到通信系统中的解码问题时,很多难题都迎刃而解。所谓语音识别,就是听话人去猜测说话者要表达的意思。好比通信系统中,根据接收端的信号去分析、理解、还原发送端传来的信息。
接收端如何解析?假设接收端的观测信息为o1,o2,...从所有的源信息中找到最可能产生出观测信息的那一个信息串s1,s2,… 就是信号源发送的信息。即使P(s1,s2,...|o1,o2,...)达到最大值的那个信息串s1,s2,… 。利用贝叶斯变换成: P(o1,o2,...|s1,s2,...)⋅P(s1,s2,...)/P(o1,o2,...)。其中P(o1,o2,...)为可以忽略的常数,因此上面公式等价为P(o1,o2,...|s1,s2,...)⋅P(s1,s2,...)--(a)。 这个公式可以由隐含马尔科夫模型来估计。
HMM基于两个假设
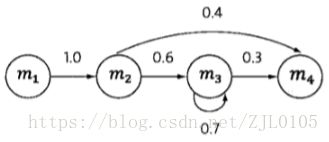
马尔科夫假设-随机过程中各个状态st的概率分布,只与它的前一个状态st−1有关, 即P(st|s1,s2,...,st−1)=P(st|st−1)。符合这个假设的随机过程称为马尔科夫过程,也称马尔科夫链。
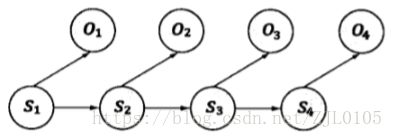
隐含马尔科夫模型是上述马尔科夫链的一个扩展:任一时刻t的状态st是不可见的,但在每个时刻t会输出一个符号ot是可见的。
独立输出假设-ot跟st相关且仅跟st相关,即任意时刻的观测只依赖于该时刻马尔可夫链状态,与其他观测及状态无关。
基于马尔科夫假设和独立输出假设,我们可以计算出某个特定的状态序列s1,s2,...产生出输出符号o1,o2,...的概率。
我们把马尔科夫假设和独立输出假设应用于通信解码问题,即把下面两式代入(a)后同上式相同。
通信解码问题就可以用HMM来解决。很多自然语言处理问题和通信解码是等价的,所以它们也可以用HMM来解决。P (o1,o2,o3,…|s1,s2,s3….) 根据应用的不同而又不同的名称,在语音识别中它被称为“声学模型” (Acoustic Model), 在机器翻译中是“翻译模型” (Translation Model) 而在拼写校正中是“纠错模型” (Correction Model)。
模型训练
三组参数
要确定一个 HMM,除了要指定其对应的状态空间 S 和观测空间 O 之外,还需要三组参数,分别是:
- 状态转移概率:模型在各个状态间转换的概率,通常记作矩阵 A=[aij]N×N。其中,aij=P(st+1=Sj|st=Si),1⩽i,j⩽N 表示在任意时刻 t,若状态为 Si,则下一时刻状态为 Sj 的概率。
- 输出观测概率:模型根据当前状态获得各个观测值的概率,通常记作矩阵 B=[bij]N×M。其中,bij=P(ot=Oj|st=Si),1⩽i⩽N,1⩽j⩽M 表示在任意时刻 t,若状态为 Si,则观测值 Oj 被获取的概率。
- 初始状态概率:模型在初始时刻各状态出现的概率,通常记作 π=(π1,π2,...,πN),其中 πi=P(s1=Si),1⩽i⩽N 表示模型的初始状态为 Si 的概率。
通常我们用 λ=[A,B,π] 来指代这三组参数。
三个基本问题
在实际应用中,HMM常见的三个问题:
概率计算问题又称评价(Evaluation)问题。
已知信息:
- 模型 λ=[A,B,π]
- 观测序列 O=(o1,o2,…,oT)
求解目标:某个特定观测序列 O 出现的概率:P(O|λ)。也就是说,求给定观测序列和给定模型之间的匹配度。
常用算法:前向/后向算法(Forward-Backward)
预测问题又称解码(Decoding)问题。
已知信息:
- 模型 λ=[A,B,π]
- 观测序列 O=(o1,o2,…,oT)
求解目标:使观测序列 O 条件概率 P(O|S) 最大的状态序列 S=(s1,s2,…,sT)。即给定观测序列,求最有可能产生这个输出的状态序列。
常用算法:维特比算法。它是一种动态规划方法,其核心思想是:如果最终的最优路径经过某个Oi,那么从初始节点到Oi-1点路径必然也是一个最优路径-因为每个节点Oi只会影响前后两个P(Oi-1|Oi)和P(Oi|Oi+1)(二元模型)。
学习问题又称训练(Training)问题。
已知信息:
- 观测序列 O=(o1,o2,…,oT)
- 或许也会给定与之对应的状态序列: S=(s1,s2,…,sT)
求解目标:估计模型 λ=[A,B,π] 参数,使得该模型下观测序列概率 P(O|λ) 最大。也就是给定足够量的观测数据,如何估计隐马尔科夫模型的参数。
常用算法:根据训练数据的不同,可以分为有监督学习和无监督学习两种。如果训练数据既包括观测序列,又包括对应的状态序列,且两者之间的对应关系已经明确标注了出来,那么就可以用有监督学习算法。我们可以用频数来估计概率;当训练数据仅有观测序列(设观测序列为 O),而没有与其对应的状态序列时,使用专门的无监督训练算法-鲍姆-韦尔奇算法(Baum-Welch Algorithm)
前两个问题是模型已经存在之后如何使用模型的问题,而最后一个则是如何通过训练得到模型的问题。
参考
周志华--机器学习
吴军--数学之美