LeetCode题解 - 双指针
文章目录
- LeetCode题解 - 双指针
-
- 一、快慢指针的常见算法
-
- 141. 环形链表(简单)
- 142. 环形链表II (中等)
- 876. 链表的中间节点(简单)
- 剑指offer 22. 链表中倒数第k个节点(简单)
- 二、左右指针的常用算法
-
- 1. 二分查找
- 167. 两数之和 II - 输入有序数组(简单)
- 633. 平方数之和(中等)
- 344. 反转字符串(简单)
- 345. 反转字符串中的元音字母(简单)
- 541. 反转字符串 II (简单)
- 189. 旋转数组(中等)
- 680. 验证回文串 II (简单)
- 88. 合并两个有序数组(简单)
- 524. 通过删除字母匹配到字典里最长单词(中等)
- 三、滑动窗口算法
-
- 76. 最小覆盖子串(困难)
- 567. 字符串的排列(中等)
- 438. 找到字符串中所有字母异位词(中等)
- 3. 无重复字串的最长子串(中等)
讲解部分参考:作者:labuladong 公众号:labuladong
labuladong的算法小抄pdf_双指针技巧直接秒杀五道算法题
labuladong的算法小抄pdf_我写了一套框架,把滑动窗口算法变成了默写题
LeetCode题解 - 双指针
双指针技巧还可以分为两类,一类是「快慢指针」,一类是「左右指针」。前者解决主要解决链表中的问题,比如典型的判定链表中是否包含环;后者主要解决数组(或者字符串)中的问题,比如二分查找。
一、快慢指针的常见算法
快慢指针一般都初始化指向链表的头结点 head,前进时快指针 fast 在前,慢指针 slow 在后,巧妙解决一些链表中的问题。
141. 环形链表(简单)
给定一个链表,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
如果链表中存在环,则返回 true 。 否则,返回 false

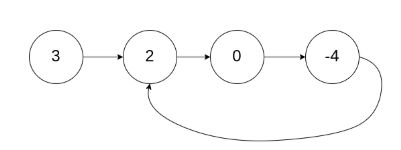
输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。
解题思路:
这应该属于链表最基本的操作了。单链表的特点是每个节点只知道下一个节点,所以一个指针的话无法判断链表中是否含有环的。经典解法就是用两个指针,一个每次前进两步,一个每次前进一步。如果不含有环,跑得快的那个指针最终会遇到 null,说明链表不含环;如果含有环,快指针最终会超慢指针一圈,和慢指针相遇,说明链表含有环。
public class Solution {
public boolean hasCycle(ListNode head) {
ListNode fast = head;
ListNode slow = head;
while(fast != null && fast.next != null){
slow = slow.next;
fast = fast.next.next;
if(fast == slow) return true;
}
return false;
}
}
142. 环形链表II (中等)
给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。注意,pos 仅仅是用于标识环的情况,并不会作为参数传递到函数中。
输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
解题思路:
第一次相遇时,假设慢指针 slow 走了 k 步,那么快指针 fast 一定走了 2k 步,也就是说比 slow 多走了 k 步(也就是环的长度)。
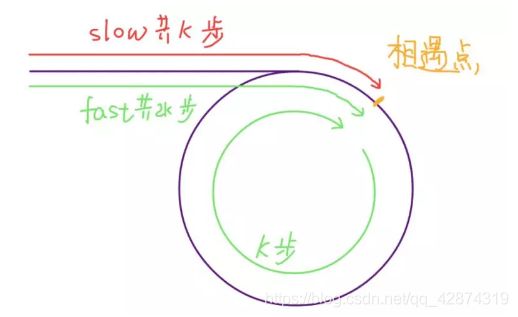
设相遇点距环的起点的距离为 m,那么环的起点距头结点 head 的距离为 k - m,也就是说如果从 head 前进 k - m 步就能到达环起点。
巧的是,如果从相遇点继续前进 k - m 步,也恰好到达环起点。

所以,当快慢指针相遇时,让其中任一个指针重新指向头节点,然后让它俩以相同速度前进,k - m 步后就会相遇,再次相遇时所在的节点位置就是环开始的位置。
public class Solution {
public ListNode detectCycle(ListNode head) {
ListNode slow = head;
ListNode fast = head;
while(fast != null && fast.next != null){
slow = slow.next;
fast = fast.next.next;
if(fast == slow){
slow = head;
while(slow != fast){
slow = slow.next;
fast = fast.next;
}
return slow;
}
}
return null;
}
}
876. 链表的中间节点(简单)
给定一个头结点为 head 的非空单链表,返回链表的中间结点。
如果有两个中间结点,则返回第二个中间结点。
输入:[1,2,3,4,5]
输出:此列表中的结点 3 (序列化形式:[3,4,5])
返回的结点值为 3 。 (测评系统对该结点序列化表述是 [3,4,5])。
注意,我们返回了一个 ListNode 类型的对象 ans,这样:
ans.val = 3, ans.next.val = 4, ans.next.next.val = 5, 以及 ans.next.next.next = NULL.
解题思路:
类似上面的思路,我们还可以让快指针一次前进两步,慢指针一次前进一步,当快指针到达链表尽头时,慢指针就处于链表的中间位置。
当链表的长度是奇数时,slow 恰巧停在中点位置;如果长度是偶数,slow 最终的位置是中间偏右:

class Solution {
public ListNode middleNode(ListNode head) {
ListNode slow = head;
ListNode fast = head;
while(fast != null && fast.next != null){
slow = slow.next;
fast = fast.next.next;
}
return slow;
}
}
寻找链表中点的一个重要作用是对链表进行归并排序。
回想数组的归并排序:求中点索引递归地把数组二分,最后合并两个有序数组。对于链表,合并两个有序链表是很简单的,难点就在于二分。
剑指offer 22. 链表中倒数第k个节点(简单)
输入一个链表,输出该链表中倒数第k个节点。为了符合大多数人的习惯,本题从1开始计数,即链表的尾节点是倒数第1个节点。
例如,一个链表有 6 个节点,从头节点开始,它们的值依次是 1、2、3、4、5、6。这个链表的倒数第 3 个节点是值为 4 的节点
给定一个链表: 1->2->3->4->5, 和 k = 2.
返回链表 4->5.
解题思路:
我们的思路还是使用快慢指针,让快指针先走 k 步,然后快慢指针开始同速前进。这样当快指针走到链表末尾 null 时,慢指针所在的位置就是倒数第 k 个链表节点(为了简化,假设 k 不会超过链表长度):
class Solution {
public ListNode getKthFromEnd(ListNode head, int k) {
ListNode slow = head;
ListNode fast = head;
while(k > 0){
fast = fast.next;
k--;
}
while(fast != null){
slow = slow.next;
fast = fast.next;
}
return slow;
}
}
二、左右指针的常用算法
左右指针在数组中实际是指两个索引值,一般初始化为 left = 0, right = nums.length - 1 。
1. 二分查找
前文 二分查找算法详解 有详细讲解,这里只写最简单的二分算法,旨在突出它的双指针特性:
int binarySearch(int[] nums, int target) {
int left = 0;
int right = nums.length - 1; // 注意
while(left <= right) {
// 注意
int mid = left + (right - left) / 2;
if(nums[mid] == target)
return mid;
else if (nums[mid] < target)
left = mid + 1; // 注意
else if (nums[mid] > target)
right = mid - 1; // 注意
}
return -1;
}
167. 两数之和 II - 输入有序数组(简单)
给定一个已按照 升序排列 的整数数组 numbers ,请你从数组中找出两个数满足相加之和等于目标数 target 。
函数应该以长度为 2 的整数数组的形式返回这两个数的下标值*。*numbers 的下标 从 1 开始计数 ,所以答案数组应当满足 1 <= answer[0]
你可以假设每个输入只对应唯一的答案,而且你不可以重复使用相同的元素。
输入:numbers = [2,7,11,15], target = 9
输出:[1,2]
解释:2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。
输入:numbers = [2,3,4], target = 6
输出:[1,3]
只要数组有序,就应该想到双指针技巧。这道题的解法有点类似二分查找,通过调节 left 和 right 可以调整 sum 的大小:
class Solution {
public int[] twoSum(int[] numbers, int target) {
if(numbers == null || numbers.length == 0){
return new int[]{
-1, -1};
}
int left = 0, right = numbers.length - 1;
while(left <= right){
int sum = numbers[left] + numbers[right];
if(sum < target){
left ++;
}else if(sum > target){
right --;
}else{
return new int[]{
left + 1, right + 1};
}
}
return new int[]{
-1, -1};
}
}
633. 平方数之和(中等)
给定一个非负整数 c ,你要判断是否存在两个整数 a 和 b,使得 a2 + b2 = c 。
输入:c = 5
输出:true
解释:1 * 1 + 2 * 2 = 5
输入:c = 3
输出:false
解题思路:本题和 167. Two Sum II - Input array is sorted 类似,只有一个明显区别:一个是和为 target,一个是平方和为 target。本题同样可以使用双指针得到两个数,使其平方和为 target。
本题的关键是右指针的初始化,实现剪枝,从而降低时间复杂度。设右指针为 x,左指针固定为 0,为了使 0^2+ x^2 的值尽可能接近 target,我们可以将 x 取为 sqrt(target)。
因为最多只需要遍历一次 0~sqrt(target),所以时间复杂度为 O(sqrt(target))。又因为只使用了两个额外的变量,因此空间复杂度为 O(1)。
class Solution {
public boolean judgeSquareSum(int c) {
int left = 0, right = (int)Math.sqrt(c);
while(left <= right){
int sum = left * left + right * right;
if(sum == c){
return true;
}else if(sum > c){
right--;
}else{
left++;
}
}
return false;
}
}
344. 反转字符串(简单)
编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。
不要给另外的数组分配额外的空间,你必须**原地修改输入数组**、使用 O(1) 的额外空间解决这一问题。
你可以假设数组中的所有字符都是 ASCII 码表中的可打印字符。
输入:["h","e","l","l","o"]
输出:["o","l","l","e","h"]
class Solution {
public void reverseString(char[] s) {
int left = 0, right = s.length - 1;
while(left <= right){
char temp = s[left];
s[left] = s[right];
s[right] = temp;
left++;
right--;
}
}
}
345. 反转字符串中的元音字母(简单)
编写一个函数,以字符串作为输入,反转该字符串中的元音字母。
输入:"hello"
输出:"holle"
解题思路:注意这里输入的是字符串,Java是以String类型的对象来实现字符串。String是一个类,当创建一个String对象后,所创建的字符串是不能改变的。在需要使用可修改的字符串时,Java提供两个选择—StringBuffer和StringBuilder。
在本题中,我们可以将字符串转换为字符数组进行交换,如上题所示,最后新建一个新的字符串返回即可。
class Solution {
HashSet<Character> vowels = new HashSet<>(
Arrays.asList('a', 'e', 'i', 'o', 'u', 'A', 'E', 'I', 'O', 'U'));
public String reverseVowels(String s) {
int left = 0, right = s.length() - 1;
char[] arr = s.toCharArray();
while(left <= right){
char c1 = arr[left];
char c2 = arr[right];
if(!vowels.contains(c1)){
left++;
}else if(!vowels.contains(c2)){
right--;
}else{
//转换成字符数组后进行交换操作
char temp = arr[left];
arr[left++] = arr[right];
arr[right--] = temp;
}
}
return new String(arr);
}
}
541. 反转字符串 II (简单)
给定一个字符串 s 和一个整数 k,你需要对从字符串开头算起的每隔 2k 个字符的前 k 个字符进行反转。
-
如果剩余字符少于
k个,则将剩余字符全部反转。 -
如果剩余字符小于
2k但大于或等于k个,则反转前k个字符,其余字符保持原样。
输入: s = "abcdefg", k = 2
输出: "bacdfeg"
class Solution {
public String reverseStr(String s, int k) {
char[] a = s.toCharArray();
for(int i = 0; i < a.length; i = i + 2*k){
int left = i, right = Math.min(i + k - 1, a.length - 1);//注意此处
while(left <= right){
char temp = a[left];
a[left] = a[right];
a[right] = temp;
left++;
right--;
}
}
return new String(a);
}
}
189. 旋转数组(中等)
给定一个数组,将数组中的元素向右移动 k 个位置,其中 k 是非负数。
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右旋转 1 步: [7,1,2,3,4,5,6]
向右旋转 2 步: [6,7,1,2,3,4,5]
向右旋转 3 步: [5,6,7,1,2,3,4]
解题思路一:使用额外的数组
我们可以使用额外的数组来将每个元素放至正确的位置。用 n 表示数组的长度,我们遍历原数组,将原数组下标为 i 的元素放至新数组下标为 (i+k)% n 的位置,最后将新数组拷贝至原数组即可。
class Solution {
public void rotate(int[] nums, int k) {
int n = nums.length;
int[] temp = new int[n];
for(int i = 0; i < n; i++){
temp[(i + k) % n] = nums[i];
}
for(int i = 0; i < n; i++){
nums[i] = temp[i];
}
}
}
解题思路二:翻转数组
该方法为数组的翻转:我们可以先将所有元素翻转,这样尾部的 k % n 个元素就被移至数组头部,然后我们再翻转 [0,k % n − 1]区间的元素和 [k % n, n - 1] 区间的元素即能得到最后的答案。
class Solution {
public void rotate(int[] nums, int k) {
int n = nums.length;
reverse(nums, 0, n - 1);
reverse(nums, 0, k % n - 1);
reverse(nums, k % n, n - 1);
}
private void reverse(int[] nums, int left, int right){
while(left <= right){
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
left++;
right--;
}
}
}
作者:LeetCode-Solution
参考链接
来源:力扣(LeetCode)
680. 验证回文串 II (简单)
给定一个非空字符串 s,最多删除一个字符。判断是否能成为回文字符串。
输入: "aba"
输出: True
输入: "abca"
输出: True
解释: 你可以删除c字符。
解题思路:使用双指针可以很容易判断一个字符串是否是回文字符串:令一个指针从左到右遍历,一个指针从右到左遍历,这两个指针同时移动一个位置,每次都判断两个指针指向的字符是否相同,如果都相同,字符串才是具有左右对称性质的回文字符串。
本题的关键是处理删除一个字符。在使用双指针遍历字符串时,如果出现两个指针指向的字符不相等的情况,我们就试着删除一个字符,再判断删除完之后的字符串是否是回文字符串。
在试着删除字符时,我们既可以删除左指针指向的字符,也可以删除右指针指向的字符。
class Solution {
public boolean validPalindrome(String s) {
int left = 0, right = s.length() -1;
while(left < right){
if(s.charAt(left) != s.charAt(right)){
return isValid(s, left, right - 1) || isValid(s, left + 1, right);
}
left++;
right--;
}
return true;
}
private boolean isValid(String s, int left, int right){
while(left < right){
if(s.charAt(left) != s.charAt(right)){
return false;
}
left++;
right--;
}
return true;
}
}
88. 合并两个有序数组(简单)
给你两个有序整数数组 nums1 和 nums2,请你将 nums2 合并到 nums1 中*,*使 nums1 成为一个有序数组。
初始化 nums1 和 nums2 的元素数量分别为 m 和 n 。你可以假设 nums1 的空间大小等于 m + n,这样它就有足够的空间保存来自 nums2 的元素。
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出:[1,2,2,3,5,6]
解题思路:可以使用双指针方法。这一方法将两个数组看作队列,每次从两个数组头部取出比较小的数字放到结果中。
方法一:为两个数组分别设置一个指针 p1 与 p2 来作为队列的头部指针
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
int p1 = 0, p2 = 0;
int[] sorted = new int[m + n];
int cur;
while(p1 < m || p2 < n){
if(p1 == m){
cur = nums2[p2++];
}else if(p2 == n){
cur = nums1[p1++];
}else if(nums1[p1] < nums2[p2]){
cur = nums1[p1++];
}else{
cur = nums2[p2++];
}
sorted[p1 + p2 - 1] = cur;
}
for(int i = 0; i < m + n; ++i) {
nums1[i] = sorted[i];
}
}
}
方法二:方法一中,之所以要使用临时变量,是因为如果直接合并到数组 nums1中,nums1中的元素可能会在取出之前被覆盖。那么如何直接避免覆盖 nums1中的元素呢?观察可知,nums1 的后半部分是空的,可以直接覆盖而不会影响结果。因此可以指针设置为从后向前遍历,每次取两者之中的较大者放进 nums1的最后面。
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
int p1 = m - 1, p2 = n - 1;
int index = n + m - 1;
int cur;
while(p1 >= 0 || p2 >= 0){
if(p1 < 0){
cur = nums2[p2--];
}else if(p2 < 0){
cur = nums1[p1--];
}else if(nums1[p1] < nums2[p2]){
cur = nums2[p2--];
}else{
cur = nums1[p1--];
}
nums1[index--] = cur;
}
}
}
524. 通过删除字母匹配到字典里最长单词(中等)
给定一个字符串和一个字符串字典,找到字典里面最长的字符串,该字符串可以通过删除给定字符串的某些字符来得到。如果答案不止一个,返回长度最长且字典顺序最小的字符串。如果答案不存在,则返回空字符串。
输入:
s = "abpcplea", d = ["ale","apple","monkey","plea"]
输出:
"apple"
解题思路:一个字符串可以通过删除给定字符串的某些字符来得到,说明该字符串是给定字符串的子序列,我们可以使用双指针来判断一个字符串是否为另一个字符串的子序列。
注意题目中要求的字典顺序最小,字典顺序是按照字母ASCII顺序大小比较 ,可以使用 longestWord.compareTo(d) 来比较,若大于0,说明d的字典顺序较小。
class Solution {
public String findLongestWord(String s, List<String> dictionary) {
String longestWord = "";
for(String d : dictionary){
if(isWord(s, d)){
//如果d的长度大于最长单词的长度,或者d的长度与最长单词长度相等,但是字典序小于它的字典序,则更新最长单词
if(d.length() > longestWord.length() || (d.length() == longestWord.length() && longestWord.compareTo(d) > 0)){
longestWord = d;
}
}
}
return longestWord;
}
private boolean isWord(String s, String d){
int i = 0, j = 0;
while(i < s.length() && j < d.length()){
if(s.charAt(i) == d.charAt(j)){
j++;
}
i++;
}
return j == d.length();
}
}
三、滑动窗口算法
这也许是双指针技巧的最高境界了,如果掌握了此算法,可以解决一大类子字符串匹配的问题,不过「滑动窗口」算法比上述的这些算法稍微复杂些。
幸运的是,这类算法是有框架模板的,下篇文章就准备讲解「滑动窗口」算法模板,帮大家秒杀几道 LeetCode 子串匹配的问题。
/* 滑动窗口算法框架 */
void slidingWindow(string s, string t) {
unordered_map<char, int> need, window;
for (char c : t) need[c]++;
int left = 0, right = 0;
int valid = 0;
while (right < s.size()) {
// c 是将移入窗口的字符
char c = s[right];
// 右移窗口
right++;
// 进行窗口内数据的一系列更新
...
/*** debug 输出的位置 ***/
printf("window: [%d, %d)\n", left, right);
/********************/
// 判断左侧窗口是否要收缩
while (window needs shrink) {
// d 是将移出窗口的字符
char d = s[left];
// 左移窗口
left++;
// 进行窗口内数据的一系列更新
...
}
}
}
其中两处...表示的更新窗口数据的地方,到时候你直接往里面填就行了。
而且,这两个...处的操作分别是右移和左移窗口更新操作,等会你会发现它们操作是完全对称的。
下面就直接上四道 LeetCode 原题来套这个框架
76. 最小覆盖子串(困难)
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。
**注意:**如果 s 中存在这样的子串,我们保证它是唯一的答案。
输入:s = "ADOBECODEBANC", t = "ABC"
输出:"BANC"
解题思路:
如果我们使用暴力解法,代码大概是这样的:
for (int i = 0; i < s.size(); i++)
for (int j = i + 1; j < s.size(); j++)
if s[i:j] 包含 t 的所有字母:
更新答案
思路很直接,但是显然,这个算法的复杂度肯定大于 O(N^2) 了,不好。
滑动窗口算法的思路是这样:
***1、***我们在字符串S中使用双指针中的左右指针技巧,初始化left = right = 0,把索引左闭右开区间[left, right)称为一个「窗口」。
***2、***我们先不断地增加right指针扩大窗口[left, right),直到窗口中的字符串符合要求(包含了T中的所有字符)。
***3、***此时,我们停止增加right,转而不断增加left指针缩小窗口[left, right),直到窗口中的字符串不再符合要求(不包含T中的所有字符了)。同时,每次增加left,我们都要更新一轮结果。
***4、***重复第 2 和第 3 步,直到right到达字符串S的尽头。
这个思路其实也不难,**第 2 步相当于在寻找一个「可行解」,然后第 3 步在优化这个「可行解」,最终找到最优解,**也就是最短的覆盖子串。左右指针轮流前进,窗口大小增增减减,窗口不断向右滑动,这就是「滑动窗口」这个名字的来历。
下面画图理解一下,needs和window相当于计数器,分别记录T中字符出现次数和「窗口」中的相应字符的出现次数。
初始状态:

增加right,直到窗口[left, right)包含了T中所有字符:
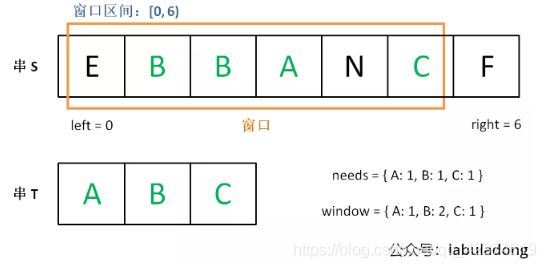
现在开始增加left,缩小窗口[left, right)。

直到窗口中的字符串不再符合要求,left不再继续移动。

之后重复上述过程,先移动right,再移动left…… 直到right指针到达字符串S的末端,算法结束。
class Solution {
public String minWindow(String s, String t) {
Map<Character,Integer> window = new HashMap(); // 用来记录窗口中的字符和数量
Map<Character,Integer> need = new HashMap(); // 需要凑齐的字符和数量
// 构建need字符集
for (char c : t.toCharArray()) {
need.put(c,need.getOrDefault(c,0)+1);
}
int left = 0,right = 0,valid = 0;
// valid是用来记录窗口中满足need要求的字符和数量的数目,比如need中要求字符a数量为2,如果window中的a字符的数量等于了2,valid就+1
int len = Integer.MAX_VALUE; // 记录最小字串的长度
int start = 0; // 记录最小字串的起始位置
while(right < s.length()){
char addChar = s.charAt(right); // 即将要加入window的字符
right++;
// 如果加入的字符是need中要求的字符,并且该字符个数已经达到了need要求的个数,则valid+1
// 这里和下面都有个坑,window.get(addChar)和need.get(addChar)返回的都是对象,最好用.equals()方法比较大小
if(need.containsKey(addChar)){
window.put(addChar,window.getOrDefault(addChar,0) + 1);
if(window.get(addChar).equals(need.get(addChar))){
valid++;
}
}
// 当window中记录的字符和数量满足了need中要求的字符和数量,考虑缩窗口
while(valid == need.size()){
// 先判断当前的最小覆盖字串是否比之前的最小覆盖字串短
if(right - left < len){
// 注意,这里上面已经对right实施了++操作,所以这里的长度不是right - left + 1
len = right - left ;
start = left; // 如果最短,则记录下该最小覆盖字串的起始位置
}
char removeChar = s.charAt(left);// removeChar是将移出窗口的字符
left++;
// 开始缩减窗口,left右移,如果要从window删除的字符正好是need中需要的并且,数目也等于need中需要的数目,
// 则删减后,该字符要求的数量显然不满足need要求的数量,所以valid要-1;
if(need.containsKey(removeChar)){
if(window.get(removeChar).equals(need.get(removeChar))){
valid--;
}
window.put(removeChar,window.get(removeChar) - 1);
}
}
}
// 如果最小覆盖字串的长度相对于定义时没变,则t不包含s中所有的字符,返回"",如果长度改变过,说明存在这样的最小覆盖字串,直接输出。
return len == Integer.MAX_VALUE? "" : s.substring(start, start + len);
}
}
需要注意的是,当我们发现某个字符在window的数量满足了need的需要,就要更新valid,表示有一个字符已经满足要求。而且,你能发现,两次对窗口内数据的更新操作是完全对称的。
当valid == need.size()时,说明T中所有字符已经被覆盖,已经得到一个可行的覆盖子串,现在应该开始收缩窗口了,以便得到「最小覆盖子串」。
移动left收缩窗口时,窗口内的字符都是可行解,所以应该在收缩窗口的阶段进行最小覆盖子串的更新,以便从可行解中找到长度最短的最终结果。
567. 字符串的排列(中等)
给定两个字符串 s1 和 s2,写一个函数来判断 s2 是否包含 s1 的排列。
换句话说,第一个字符串的排列之一是第二个字符串的 子串 。
输入: s1 = "ab" s2 = "eidbaooo"
输出: True
解释: s2 包含 s1 的排列之一 ("ba").
输入: s1= "ab" s2 = "eidboaoo"
输出: False
解题思路:
对于这道题的解法代码,基本上和最小覆盖子串一模一样,只需要改变两个地方:
**1、**本题移动left缩小窗口的时机是窗口大小大于t.size()时,因为排列嘛,显然长度应该是一样的。
**2、**当发现valid == need.size()时,就说明窗口中就是一个合法的排列,所以立即返回true。
至于如何处理窗口的扩大和缩小,和最小覆盖子串完全相同。
class Solution {
public boolean checkInclusion(String s1, String s2) {
Map<Character, Integer> need = new HashMap<>();
Map<Character, Integer> window = new HashMap<>();
for(char c : s1.toCharArray()){
need.put(c, need.getOrDefault(c, 0) + 1);
}
int left = 0, right = 0, valid = 0;
while(right < s2.length()){
char addChar = s2.charAt(right);
right++;
/// 进行窗口内数据的一系列更新
if(need.containsKey(addChar)){
window.put(addChar, window.getOrDefault(addChar, 0) + 1);
if(window.get(addChar).equals(need.get(addChar))){
valid++;
}
}
//移动left缩小窗口的时机是窗口大小大于t.size()时,因为排列嘛,显然长度应该是一样的。
while (right - left >= s1.length()){
if(valid == need.size()){
// 完全匹配返回true
return true;
}
char removeChar = s2.charAt(left);
left++;
// 进行窗口内数据的一系列更新
if(need.containsKey(removeChar)){
if(window.get(removeChar).equals(need.get(removeChar))){
valid--;
}
window.put(removeChar,window.getOrDefault(removeChar,0) -1);
}
}
}
return false;
}
}
438. 找到字符串中所有字母异位词(中等)
给定一个字符串 s 和一个非空字符串 p,找到 s 中所有是 p 的字母异位词的子串,返回这些子串的起始索引。字符串只包含小写英文字母,并且字符串 s 和 p 的长度都不超过 20100。
说明:
- 字母异位词指字母相同,但排列不同的字符串。
- 不考虑答案输出的顺序。
输入:
s: "cbaebabacd" p: "abc"
输出:
[0, 6]
解释:
起始索引等于 0 的子串是 "cba", 它是 "abc" 的字母异位词。
起始索引等于 6 的子串是 "bac", 它是 "abc" 的字母异位词。
解题思路:相当于,输入一个串s,一个串p,找到s中所有t的排列,返回它们的起始索引。跟寻找字符串的排列一样,只是找到一个合法异位词(排列)之后将起始索引加入res即可。
class Solution {
public List<Integer> findAnagrams(String s, String p) {
List<Integer> res = new ArrayList<>();
Map<Character, Integer> need = new HashMap<>();
Map<Character, Integer> window = new HashMap<>();
for(char c : p.toCharArray()){
need.put(c, need.getOrDefault(c, 0) + 1);
}
int left = 0, right = 0, valid = 0;
while(right < s.length()){
char addChar = s.charAt(right);
right++;
if(need.containsKey(addChar)){
window.put(addChar, window.getOrDefault(addChar, 0) + 1);
if(window.get(addChar).equals(need.get(addChar))){
valid++;
}
}
while(right - left == p.length()){
// 当窗口符合条件时,把起始索引加入 res
if(valid == need.size()){
res.add(left);
}
char removeChar = s.charAt(left);
left++;
if(need.containsKey(removeChar)){
if(window.get(removeChar).equals(need.get(removeChar))){
valid--;
}
window.put(removeChar, window.getOrDefault(removeChar, 0) - 1);
}
}
}
return res;
}
}
3. 无重复字串的最长子串(中等)
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1
解题思路:这就是变简单了,连need和valid都不需要,而且更新窗口内数据也只需要简单的更新计数器window即可。
当window[c]值大于 1 时,说明窗口中存在重复字符,不符合条件,就该移动left缩小窗口了嘛。
唯一需要注意的是,在哪里更新结果res呢?我们要的是最长无重复子串,哪一个阶段可以保证窗口中的字符串是没有重复的呢?
这里和之前不一样,要在收缩窗口完成后更新res,因为窗口收缩的 while 条件是存在重复元素,换句话说收缩完成后一定保证窗口中没有重复嘛。
class Solution {
public int lengthOfLongestSubstring(String s) {
Map<Character, Integer> window = new HashMap<>();
int left = 0, right = 0;
int maxLen = 0;
while(right < s.length()){
char addChar = s.charAt(right);
right++;
window.put(addChar, window.getOrDefault(addChar, 0) + 1);
//当`window[c]`值大于 1 时,说明窗口中存在重复字符,移动left缩小窗口
while(window.get(addChar) > 1){
char removeChar = s.charAt(left);
left++;
window.put(removeChar, window.getOrDefault(removeChar, 0) - 1);
}
// 在这里更新答案
maxLen = Math.max(maxLen, right - left);
}
return maxLen;
}
}
于 1 时,说明窗口中存在重复字符,不符合条件,就该移动left缩小窗口了嘛。
唯一需要注意的是,在哪里更新结果res呢?我们要的是最长无重复子串,哪一个阶段可以保证窗口中的字符串是没有重复的呢?
这里和之前不一样,要在收缩窗口完成后更新res,因为窗口收缩的 while 条件是存在重复元素,换句话说收缩完成后一定保证窗口中没有重复嘛。
class Solution {
public int lengthOfLongestSubstring(String s) {
Map<Character, Integer> window = new HashMap<>();
int left = 0, right = 0;
int maxLen = 0;
while(right < s.length()){
char addChar = s.charAt(right);
right++;
window.put(addChar, window.getOrDefault(addChar, 0) + 1);
//当`window[c]`值大于 1 时,说明窗口中存在重复字符,移动left缩小窗口
while(window.get(addChar) > 1){
char removeChar = s.charAt(left);
left++;
window.put(removeChar, window.getOrDefault(removeChar, 0) - 1);
}
// 在这里更新答案
maxLen = Math.max(maxLen, right - left);
}
return maxLen;
}
}