【源码系列】Java中的数据结构——栈，队列，链表与LinkedList

前言

自从上次字节面试凉了之后，我就一直有这个想法，想写个源码系列的博客。无奈最近事情太多，无法真正静下心来写。原本是想暑假来好好写这个系列，但因为下周要由我来负责协会授课，所以只能在这周写完。也好，毕竟只有ddl才有效率嘛（笑哭）。

关于本系列

作为源码系列的文章，我肯定会讲讲源码，当然我也只能是作为一个菜鸟的身份，带着大家一起阅读源码，顺便说说我自己的理解。

当然了，我也不想仅限于源码，我更希望达到一种效果——让概念与实践融合。

所以在讲源码之前，我会把这个数据结构的概念通讲一遍，在这个过程中我也会尽量抛出一些问题，来帮助大家思考理解。

当然，本人技术水平有限，大佬勿喷。

注：本系列的jdk版本为1.8

一、数据结构通讲

1.链表

①链表基本介绍

在上篇讲完了数组【源码系列】Java中的数据结构——数组与ArrayList之后，我们知道了数组因为连续存储的原因，所以用下标访问时时间复杂度为O(1)。但连续存储也带来一个问题——数组对于内存条件太苛刻了，系统不可能为它之后预留一大块连续空间，所以数组的大小在一开始便确认了。

在这种情况下，数组对于增删扩容的操作并不友好，每次删除增加都伴随着后续元素的前移和后移，如果容量不够，还得进行数组的复制来达到扩容的效果。

所以数组适合于一些增删操作不怎么频繁且不会经常需要扩容的情况。

但是面对增删操作比较频繁的情况该怎么办呢？
面对这种情况，有没有一种方式可以适应这种增删操作特别平凡的情况呢？

这时候就轮到我们的链表出场了。

我们知道数组这些优缺点的根本原因在于它的存储方式——连续存储。那么我们能不能不连续存储，采取零散存储的方式来避免这种情况呢。

答案是可以的，但此时又面临着一个问题——如何访问对应的元素？

数组因为连续存储的方式可以根据下标轻而易举地确定元素的地址，可是链表是如何做的呢？

在链表中，我们把每个元素叫做结点，结点一般包括该元素的值以及指向下一个元素的指针，有了下一个元素的指针我们便可以方便地访问下一个元素的地址，这样就可以访问对应的元素了。

换个形象点的说法，我们可以把每个元素想象成一个铁链上的一个铁环，元素的指针就是那个环扣，这样我们把每个铁环环环相扣，那么便组成了一条长长的链子，而这便是链表。

（图片来自王争的数据结构与算法之美）

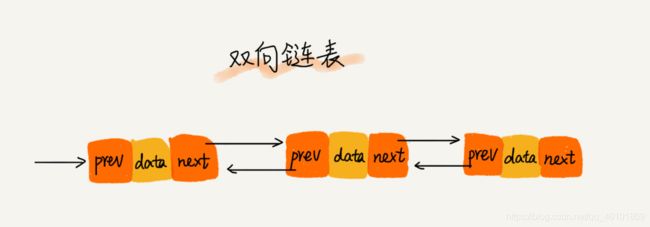
而链表的结构也五花八门，常见的有单链表，双向链表，循环链表。

（图片来自王争的数据结构与算法之美）

看图应该很快就能明白，它们的区别就在于结点之间的连接方式，或者说结点里的指针。

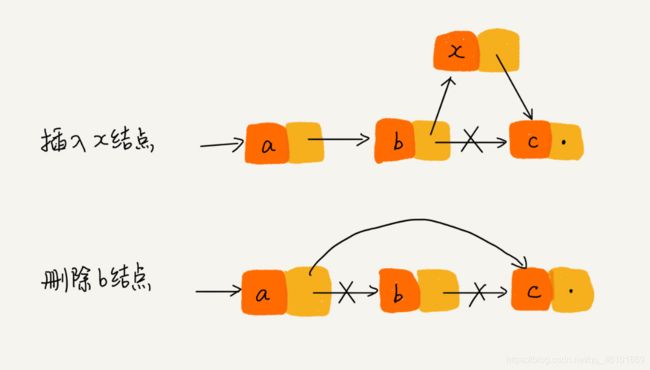
对于单链表，
如果我们要删除链表中的结点时，只需将前一个结点指针指向这个结点即可。事实上，从内存上看，这个结点并未“删除”，只是链表中指向它的指针指向了另一个结点，这样这个结点就脱离了这个链表，逻辑上就是在这个链表上删除了这个元素。

增加也同理，只需把前一个结点的指针指向新加的结点，新加的结点指针只需指向下一个结点即可。

这样链表增加删除元素实际只需做好指针重新赋值即可，时间复杂度也是O（1）。

②链表的优缺点

优点：
1.由于分散存储，对于内存的要求不高，可以有效利用现有内存空间
2.增删元素非常方便快速，只需把结点的指针重新赋值即可

缺点：
1.根据下标查询效率慢，只能一个一个遍历
2.因为每个结点还需要存储其他结点的指针，所以占用的内存空间会多一些

2.栈

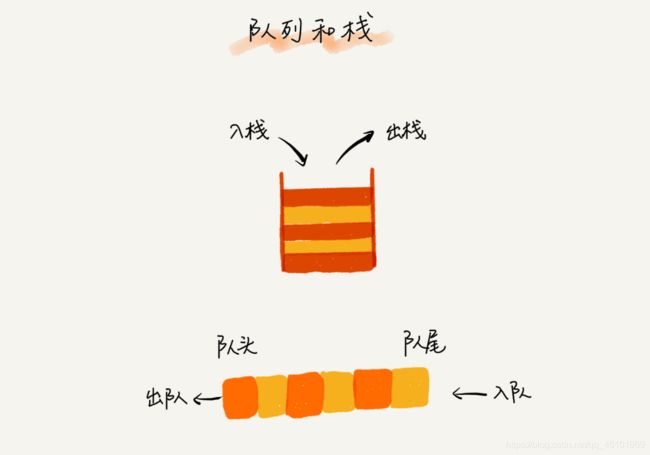
关于“栈”，你可以把它想象成一摞叠在一起的盘子。我们平时放盘子的时候，都是从下往上一个一个放；取的时候，我们也是从上往下一个一个地依次取，不能从中间任意抽出。后进者先出，先进者后出，这就是典型的“栈”结构。

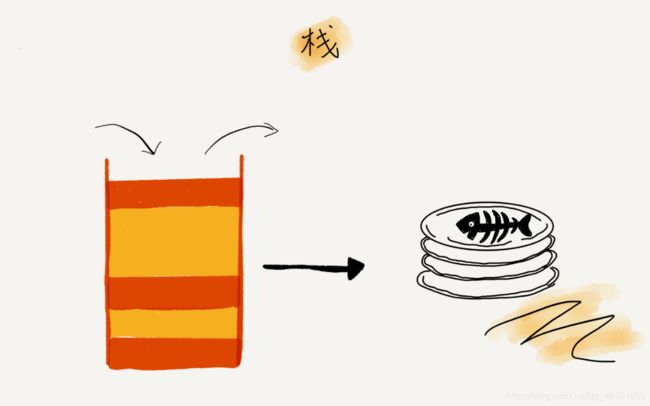
（来自王争的数据结构与算法之美）

从栈的操作特性上来看，栈是一种“操作受限”的线性表，只允许在一端插入和删除数据。

3.队列

队列这个概念非常好理解。
你可以把它想象成排队买票，先来的先买，后来的人只能站末尾，不允许插队。先进者先出，这就是典型的“队列”。

我们知道，栈只支持两个基本操作：入栈 push()和出栈 pop()。队列跟栈非常相似，支持的操作也很有限，最基本的操作也是两个：入队 enqueue()，放一个数据到队列尾部；出队 dequeue()，从队列头部取一个元素。

（来自王争的数据结构与算法之美）

所以，队列跟栈一样，也是一种操作受限的线性表数据结构。

二、LinkedList源码探究

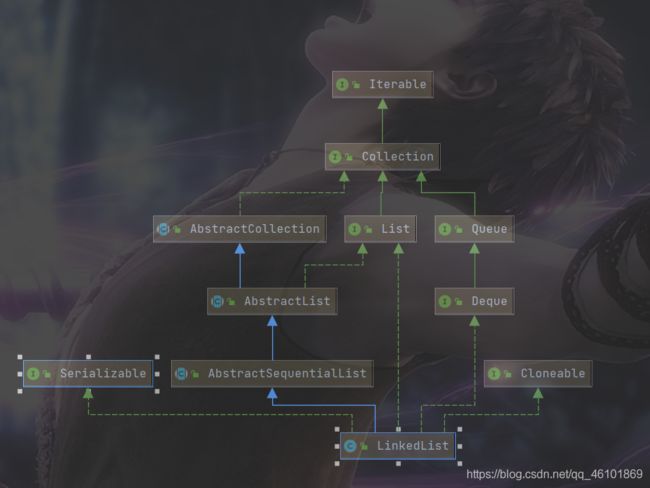
1.LinkedList继承关系

可以看到LinkedList既实现了List接口，也实现了Queue接口（队列），同时也实现了Queue的子类接口Deque接口（双向队列）。

我们前面讲队列和栈的时候讲到栈和队列都是操作受限的线性表，所以我们完全可以用链表来实现队列和栈。而这就是为什么LinkedList会实现Queue和Deque的原因，目的就是提供一个操作受限的接口供用户使用。

2.LinkedList核心原理

2.1内部类Node

private static class Node<E> {
     
		//值
        E item;
        //下一个结点的指针
        Node<E> next;
        //上一个结点的指针
        Node<E> prev;

        Node(Node<E> prev, E element, Node<E> next) {
     
            this.item = element;
            this.next = next;
            this.prev = prev;
        }
    }

这里看到结点里有两个指针，一个指向上一个结点，一个指向下一个结点，所以我们可以知道LinkedList实际上是一个双向链表。

2.2属性

	//当前list中元素的数量
	transient int size = 0;
    /**
     * 指向第一个结点的指针
     */
    transient Node<E> first;

    /**
     * 指向最后一个结点的指针
     */
    transient Node<E> last;

LinkedList对象中的属性就只有三个，事实上在所有集合类中，为了尽可能减少内存消耗，都会尽可能少地去设计属性。

2.3 构造方法

public LinkedList() {
     
}

    
public LinkedList(Collection<? extends E> c) {
     
    this();
    addAll(c);
}

一个是空构造函数，里面啥也没干；一个是创建一个LinkedList对象，然后将集合c中的元素都添加进对象中。

PS：这里并没有像ArrayList那样有规定初始大小的构造函数，因为链表容量本来就是可以增加的，所以不需要有这样的构造函数。

点开addAll（）方法

public boolean addAll(Collection<? extends E> c) {
     
        return addAll(size, c);
    }

public boolean addAll(int index, Collection<? extends E> c) {
     
        checkPositionIndex(index);
		//调用集合c的toArray方法将集合类对象转化为对象数组
        Object[] a = c.toArray();
        int numNew = a.length;
        if (numNew == 0)
            return false;

        Node<E> pred, succ;
        //找到对应下标的结点
        if (index == size) {
     
            succ = null;
            pred = last;
        } else {
     
            succ = node(index);
            pred = succ.prev;
        }
		//循环插入
        for (Object o : a) {
     
            @SuppressWarnings("unchecked") 
            E e = (E) o;
            Node<E> newNode = new Node<>(pred, e, null);
            if (pred == null)
                first = newNode;
            else
                pred.next = newNode;
            pred = newNode;
        }
		//最后一个结点的处理
        if (succ == null) {
     
            last = pred;
        } else {
     
            pred.next = succ;
            succ.prev = pred;
        }

        size += numNew;
        //修改操作计数+1
        modCount++;
        return true;
    }

大致来讲它调用了集合的toArray()方法将集合c化为数组，然后循环创建结点然后加到对应的位置，同时修改计数+1

3.List接口的常用方法

①add(E e)

public boolean add(E e) {
     
        linkLast(e);
        return true;
    }

点开linkLast方法看看，

//向尾部增加一个元素
void linkLast(E e) {
     
	//最后一个结点
    final Node<E> l = last;
    //创建一个新的结点对象
    final Node<E> newNode = new Node<>(l, e, null);
    //更新last指针为新的
    last = newNode;
    if (l == null)
        first = newNode;
    else
        l.next = newNode;
    //元素数量自增1
    size++;
    //修改的数量
    modCount++;
}

可以看到这个方法就是向尾部增加一个新的结点

②remove（Object o）

//遍历所有结点，如果是该对象则删除结点，返回true;否则返回false表示未找到
public boolean remove(Object o) {
     
        if (o == null) {
     
            for (Node<E> x = first; x != null; x = x.next) {
     
                if (x.item == null) {
     
                    unlink(x);
                    return true;
                }
            }
        } else {
     
            for (Node<E> x = first; x != null; x = x.next) {
     
                if (o.equals(x.item)) {
     
                    unlink(x);
                    return true;
                }
            }
        }
        return false;
}

我们看看unlink方法（其实从方法名称中也能知道这个方法就是解除绑定的意思），

E unlink(Node<E> x) {
     
        // assert x != null;
        final E element = x.item;
        final Node<E> next = x.next;
        final Node<E> prev = x.prev;
		
		//判断是不是首结点
        if (prev == null) {
     
        	//如果是则first指针指向下一个即可
            first = next;
        } else {
     
        	//如果不是则将前一个结点指向后一个结点
            prev.next = next;
            x.prev = null;
        }
		//判断是不是尾结点
        if (next == null) {
     
            last = prev;
        } else {
     
            next.prev = prev;
            x.next = null;
        }
		//将其值改为null,其实按理来说只需指针丢弃即可在逻辑上将结点从链表上删除，但这里可能是想让拥有这个结点指针的程序知道这个结点已经被删除了，同时把结点的值对象指针丢弃也利于gc回收
        x.item = null;
        //更新size
        size--;
        //修改计数+1
        modCount++;
        return element;
    }

这里有个有意思的地方，其实按理来说只需指针丢弃即可在逻辑上将结点从链表上删除，但这里却有个x.item=null的操作，我猜测作者可能是想让拥有这个结点指针的程序知道这个结点已经被删除了，还有就是把这个结点的对象指针丢弃可以利于gc回收（毕竟有指针指着，gc也不会强行回收掉）。

③remove(int index)

public E remove(int index) {
     
		//边界检查，就是看看index合不合法
        checkElementIndex(index);
        return unlink(node(index));
    }

这里我们可以看看node(int index)方法，

Node<E> node(int index) {
     
		//把index下标与size的一半去比较，言外之意就是比较index是在前半部分还是后半部分，这样可以较快效率
        if (index < (size >> 1)) {
     
        	//如果在前半部分便从头结点开始遍历
            Node<E> x = first;
            for (int i = 0; i < index; i++)
                x = x.next;
            return x;
        } else {
     
        	//如果在后半部分则从后半部分开始遍历
            Node<E> x = last;
            for (int i = size - 1; i > index; i--)
                x = x.prev;
            return x;
        }
    }

这个方法就是根据下标去寻找对应的元素，不过呢，这里有点小优化，他会判断这个下标是前半部分还是后半部分来选择从前往后遍历还是从后往前遍历。然后把对应的几点返回。

④set(int index, E element)

public E set(int index, E element) {
     
		//下标检查
        checkElementIndex(index);
        //查找对应的结点
        Node<E> x = node(index);
        E oldVal = x.item;
        //更新值
        x.item = element;
        //返回旧值
        return oldVal;
}

这个方法就是根据下标对对应结点值进行修改。

⑤indexOf(Object o)

public int indexOf(Object o) {
     
        int index = 0;
        if (o == null) {
     
            for (Node<E> x = first; x != null; x = x.next) {
     
                if (x.item == null)
                    return index;
                index++;
            }
        } else {
     
            for (Node<E> x = first; x != null; x = x.next) {
     
                if (o.equals(x.item))
                    return index;
                index++;
            }
        }
        return -1;
    }

该方法就是寻找该对象的下标，它会从前往后遍历，如果遇到相同值的结点就会返回第一个相同值的下标；如果没找到则返回-1；

⑥lastIndexOf(Object o)

public int lastIndexOf(Object o) {
     
        int index = size;
        if (o == null) {
     
            for (Node<E> x = last; x != null; x = x.prev) {
     
                index--;
                if (x.item == null)
                    return index;
            }
        } else {
     
            for (Node<E> x = last; x != null; x = x.prev) {
     
                index--;
                if (o.equals(x.item))
                    return index;
            }
        }
        return -1;
    }

这个方法和上面方法类似，都是返回值相同的结点下标，不过它是从后往前找，所以它会返回最后那个值相同的结点下标；若没找到则返回-1。

⑦clear()

public void clear() {
     
        // Clearing all of the links between nodes is "unnecessary", but:
        // - helps a generational GC if the discarded nodes inhabit
        //   more than one generation
        // - is sure to free memory even if there is a reachable Iterator
        for (Node<E> x = first; x != null; ) {
     
            Node<E> next = x.next;
            x.item = null;
            x.next = null;
            x.prev = null;
            x = next;
        }
        first = last = null;
        size = 0;
        modCount++;
    }

这里有一步奇怪的的操作，就是循环把每个结点里的结点指针和对象指针都设为null，源码里注释就是上面那句英文，大概意思是清除所有不需要的结点之间的联系，利于帮助gc回收。

你可能看起来很奇怪，我给你解释一下：
这步操作涉及gc的内存回收的过程，我们如何判断这块内存有没有用呢？很重要的依据就是有没有指针指向块内存。这里就是要把这种指针给消除了，把这种相互之间的联系去除了。具体的操作就是把这些无用的对象指针都变为null，这样gc就能更好的判定它是无用的，从而更早的回收掉这部分无用的内存。

4.Queue接口的常用方法

我们之前说了，队列实际上就是一个操作受限的线性表，用链表也可以实现一个队列。
事实上LinkedList就可以当做队列来操作，比如下面这样

Queue<Integer> queue=new LinkedList();
//入队
queue.add(1);
//打印队首元素
System.out.println(queue.peek());
//出队
queue.poll();

这里就是一个典型队列使用例子，Queue接口约束了其他方法，从而实现了队列那种先进先出的效果

①add(E e)

public boolean add(E e) {
     
		//创建一个值为e的结点，加到队尾
        linkLast(e);
        return true;
}

这个add方法实际上就是之前List接口里的add方法

②poll()

public E poll() {
     
        final Node<E> f = first;
        return (f == null) ? null : unlinkFirst(f);
    }

取出队首元素，实际上就是取出链表头部的元素。

③peek()

public E peek() {
     
        final Node<E> f = first;
        return (f == null) ? null : f.item;
    }

返回队首元素的值，实际上就是返回链表头部元素的值。

5.Deque接口的常用方法

Deque是个双向队列的接口，但实际上也是可以用来当做栈使用的。就像下面这样，

Deque<Integer> stack=new LinkedList();
//入栈
stack.push(1);
//输出栈顶元素
System.out.println(stack.peek());
//出栈
stack.pop();

①push(E e)

public void push(E e) {
     
        addFirst(e);
}

入栈，实际上就是往链表头部插入一个元素

②pop()

public E pop() {
     
        return removeFirst();
    }

出栈，实际上也是删除返回链表头部元素

③peek()

返回栈顶元素，
这个和Queue中一样就不展示了。

6.LinkedList迭代器

注意：LinkedList没有Iterator的实现，调用Iterator（）方法也是返回ListItr对象

①ListItr

private class ListItr implements ListIterator<E> {
     
        private Node<E> lastReturned;
        private Node<E> next;
        private int nextIndex;
        private int expectedModCount = modCount;

        ListItr(int index) {
     
            // assert isPositionIndex(index);
            next = (index == size) ? null : node(index);
            nextIndex = index;
        }

        public boolean hasNext() {
     
            return nextIndex < size;
        }

        public E next() {
     
        	//检查是否存在预期外的修改
            checkForComodification();
            //判断next是否越界
            if (!hasNext())
                throw new NoSuchElementException();
			//指针后移
            lastReturned = next;
            next = next.next;
            //下标+1
            nextIndex++;
            return lastReturned.item;
        }

        public boolean hasPrevious() {
     
            return nextIndex > 0;
        }

        public E previous() {
     
            checkForComodification();
            if (!hasPrevious())
                throw new NoSuchElementException();

            lastReturned = next = (next == null) ? last : next.prev;
            nextIndex--;
            return lastReturned.item;
        }

        public int nextIndex() {
     
            return nextIndex;
        }

        public int previousIndex() {
     
            return nextIndex - 1;
        }

        public void remove() {
     
            checkForComodification();
            if (lastReturned == null)
                throw new IllegalStateException();

            Node<E> lastNext = lastReturned.next;
            unlink(lastReturned);
            if (next == lastReturned)
                next = lastNext;
            else
                nextIndex--;
            lastReturned = null;
            expectedModCount++;
        }

        public void set(E e) {
     
            if (lastReturned == null)
                throw new IllegalStateException();
            checkForComodification();
            lastReturned.item = e;
        }

        public void add(E e) {
     
            checkForComodification();
            lastReturned = null;
            if (next == null)
                linkLast(e);
            else
                linkBefore(e, next);
            nextIndex++;
            //预期修改增加
            expectedModCount++;
        }

        public void forEachRemaining(Consumer<? super E> action) {
     
        	//检查action参数对象是否为null
            Objects.requireNonNull(action);
            //遍历执行action的accept方法，把结点的值作为参数传入
            while (modCount == expectedModCount && nextIndex < size) {
     
                action.accept(next.item);
                lastReturned = next;
                next = next.next;
                nextIndex++;
            }
            //检查是否有预期外的修改
            checkForComodification();
        }

        final void checkForComodification() {
     
            if (modCount != expectedModCount)
                throw new ConcurrentModificationException();
        }
    }

这个迭代器和ArrayList中的ListItr的套路如出一辙，唯一的区别就是LinkedList遍历是通过结点的指针不断往前。具体的可以看我前一篇【源码系列】Java中的数据结构——数组与ArrayList，里面也讲了为什么会有modcount以及迭代器是如何实现干扰检测的机制。当然这里的机制实现也有一点小的区别，在ArrayList中expectedModCount是通过expectedModCount = modCount;直接改变的，而这里是expectedModCount++。但这里我感觉区别不大，这里就不再赘述了。

当然，这里的forEachRemaining方法特别有意思，它可以支持我们用lambda表达式。从这里的源码可以看出lambda表达式的原理——看似写的是函数，实际上写的只是一个实现了对应接口的匿名内部类而已，这里的参数也并不是一个函数，而是一个接口的实现类。

②DescendingIterator 逆序迭代器

private class DescendingIterator implements Iterator<E> {
     
        private final ListItr itr = new ListItr(size());
        public boolean hasNext() {
     
            return itr.hasPrevious();
        }
        public E next() {
     
            return itr.previous();
        }
        public void remove() {
     
            itr.remove();
        }
    }

是不是很有意思，里面的实现还是ListItr，只不过next和它反着来（笑哭）。

③DescendingIterator 拆分迭代器

static final class LLSpliterator<E> implements Spliterator<E> {
     
        static final int BATCH_UNIT = 1 << 10;  // batch array size increment
        static final int MAX_BATCH = 1 << 25;  // max batch array size;
        final LinkedList<E> list; // null OK unless traversed
        Node<E> current;      // current node; null until initialized
        int est;              // size estimate; -1 until first needed
        int expectedModCount; // initialized when est set
        int batch;            // batch size for splits

        LLSpliterator(LinkedList<E> list, int est, int expectedModCount) {
     
            this.list = list;
            this.est = est;
            this.expectedModCount = expectedModCount;
        }

        final int getEst() {
     
            int s; // force initialization
            final LinkedList<E> lst;
            if ((s = est) < 0) {
     
                if ((lst = list) == null)
                    s = est = 0;
                else {
     
                    expectedModCount = lst.modCount;
                    current = lst.first;
                    s = est = lst.size;
                }
            }
            return s;
        }

        public long estimateSize() {
      return (long) getEst(); }

        public Spliterator<E> trySplit() {
     
            Node<E> p;
            int s = getEst();
            if (s > 1 && (p = current) != null) {
     
                int n = batch + BATCH_UNIT;
                if (n > s)
                    n = s;
                if (n > MAX_BATCH)
                    n = MAX_BATCH;
                Object[] a = new Object[n];
                int j = 0;
                do {
      a[j++] = p.item; } while ((p = p.next) != null && j < n);
                current = p;
                batch = j;
                est = s - j;
                return Spliterators.spliterator(a, 0, j, Spliterator.ORDERED);
            }
            return null;
        }

        public void forEachRemaining(Consumer<? super E> action) {
     
            Node<E> p; int n;
            if (action == null) throw new NullPointerException();
            if ((n = getEst()) > 0 && (p = current) != null) {
     
                current = null;
                est = 0;
                do {
     
                    E e = p.item;
                    p = p.next;
                    action.accept(e);
                } while (p != null && --n > 0);
            }
            if (list.modCount != expectedModCount)
                throw new ConcurrentModificationException();
        }

        public boolean tryAdvance(Consumer<? super E> action) {
     
            Node<E> p;
            if (action == null) throw new NullPointerException();
            if (getEst() > 0 && (p = current) != null) {
     
                --est;
                E e = p.item;
                current = p.next;
                action.accept(e);
                if (list.modCount != expectedModCount)
                    throw new ConcurrentModificationException();
                return true;
            }
            return false;
        }

        public int characteristics() {
     
            return Spliterator.ORDERED | Spliterator.SIZED | Spliterator.SUBSIZED;
        }
    }

这个拆分迭代器时jdk8引入的，是为了满足流式编程的需要，用于并行流的拆分，这块我以后再补。（未完待续…）

三、总结

链表和数组一样都是线性表的一种，不过有别于数组的连续存储，它采取零散存储的方式，尽管它会造成更多的内存消耗，但是也会带来一些数组没有的好处。而LinkedList便是链表的实现和封装。

对于LinkedList你需要记住以下几点：

1. LinedList实际是由链表实现，是一种双向链表的实现。
2. LinkedList可以是栈、队列的实现，LinkedList实现了Queue，Deque（Queue的子接口）的接口，可以分别对应队列和栈的实现，能这样做的根本原因就在于队列和栈都是一种受限制的线性表。
3. LinkedList增删操作快，时间复杂度为O(1)；但是根据下标查找元素慢，其时间复杂度为O(n)。
4. LinkedList查找下标元素时，会进行对下标进行判断，如果是前半部分就从头结点开始遍历查找，否则从尾结点开始遍历查找，这样做可以提升效率（思路有点像跳表）。
5. LinkedList适用于增删多，查询操作少的情况。
6. LinkedList迭代器中同样用modcount来进行干扰检测，提示集合迭代过程中程序出现的问题。
7. LinkedList在执行clear方法进行清除所有元素时，它会把所有元素结点的所有指针都赋值为null，这么做的目的就是使这些无用对象尽快地被gc回收。

---

好了，这篇的内容到这里就差不多结束了，当然本文也并非讲解所有的源码，只是挑了核心原理的一部分来讲，至于其他方法，个人认为是一些其他方面的封装，这里我就不一一赘述了，感兴趣的同学可以自己去研读。

愿我们以梦为马，不负人生韶华。
与君共勉！