MATLAB绘图功能
图形窗口的创建与控制,图形窗口的基本操作;二维和三维绘图基本的指令、着色、线型控制‘特殊图形表现特殊数据的性质;坐标轴的控制和图形标注命令
目录
- 1.图形窗口的创建
- 2.二维平面图形与坐标系
-
- 2.1.几个基本的绘图指令
-
- 2.1.1.线性坐标曲线plot
- 2.1.2.plot(X,Y)注意事项
- 2.1.3.plot(Z)绘图
- 2.1.4.对数坐标曲线命令
- 2.1.5.双y轴图形
- 2.2.线型和颜色
- 2.3.图形窗口的分割
- 2.4.坐标系的调整
- 3.三维绘图
-
- 3.1.三维曲线绘图指令
- 3.2.三维曲面绘图指令
-
- 3.2.1.平面网格点的生成
- 3.2.2.三维网格命令mesh
- 3.2.3.三维网格命令meshc、meshz
- 3.2.4.三维表面命令surf
- 3.2.5.等高线图形的绘制
- 3.2.6.柱面和球面的三维表达
- 4.特殊图形绘制
-
- 4.1.直方图命令 bar
- 4.2.饼图命令 pie
- 5.极坐标系下绘制图形
- 6.坐标轴的调整和图形的标注
-
- 6.1.坐标轴调整命令
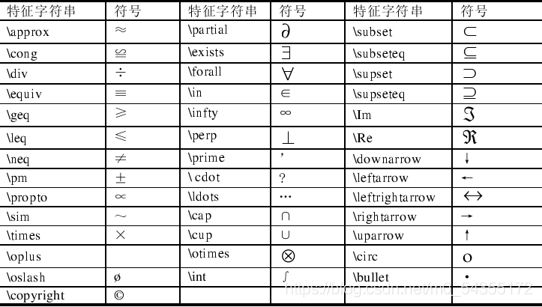
- 6.2.特征字符串中的希腊字母
- 6.3.特征字符串中的其他字符
- 6.4.图例的标注
-
- 6.4.1.图例的说明legend
- 6.4.2.控制分格线grid
- 6.4.3.标记函数text
- 6.4.4.设置坐标轴set
- 6.4.5.使用函数 xlabel、title 和 legend 命令进行标注
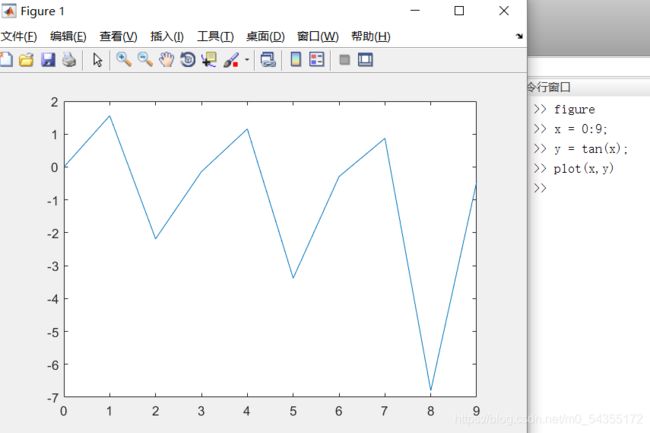
1.图形窗口的创建
- 对离散区间进行更细的划分,逐步趋近函数的连续变化特性,直到视觉上呈现连续的效果
- 把每两个离散点用直线连续,以每两个离散点之间的直线来近似表示两点间函数特性
2.二维平面图形与坐标系
2.1.几个基本的绘图指令
2.1.1.线性坐标曲线plot
plot 是 MATLAB 二维曲线绘图中最简单、最重要、使用最广泛的一个线性绘图函数。它可以生成线段、曲线和参数方程曲线的函数图形
| 指令 | 说明 |
|---|---|
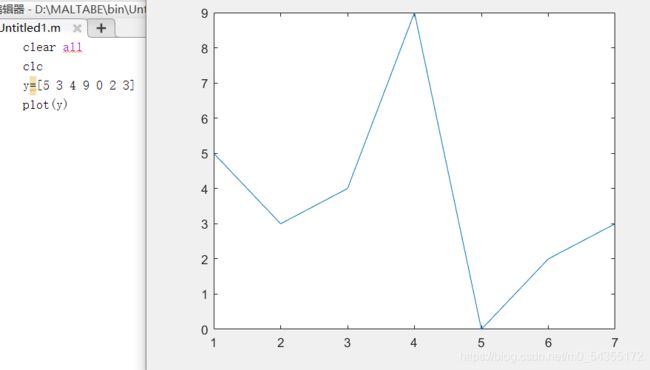
| plot(y) | 单参数式(y为纵坐标向量,横坐标为向量[1 2 3 4 …]) |
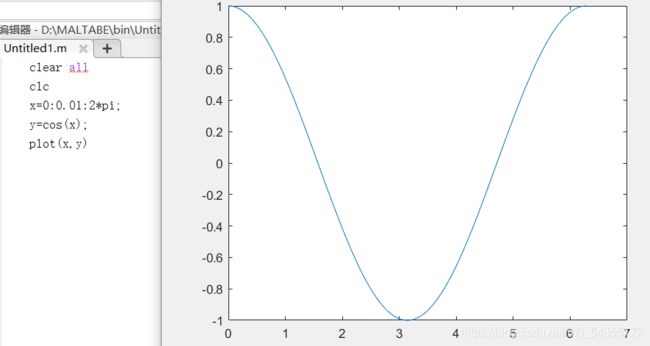
| plot(x,y) | 参数式 (x 为横坐标向量,y为纵坐标向量) |
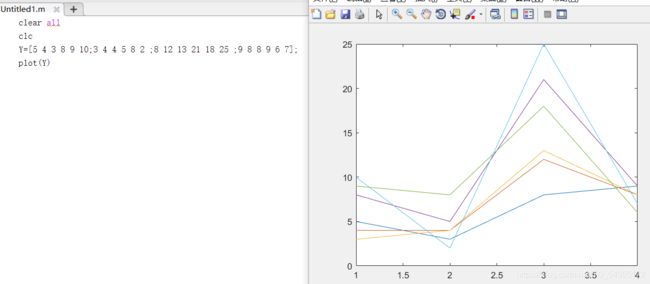
| plot(Y) | m×n 矩阵式(矩阵的每列为纵坐标,横坐标为向量[1:m]) |
| plot(X,Y) | 混合式 |
| plot(Z) | 复向量式 |
| plot(x1,y1,x2,y2,…) | 综合调用方式 |
2.1.2.plot(X,Y)注意事项
- 如果 X 和 Y 都是向量,则长度必须相等
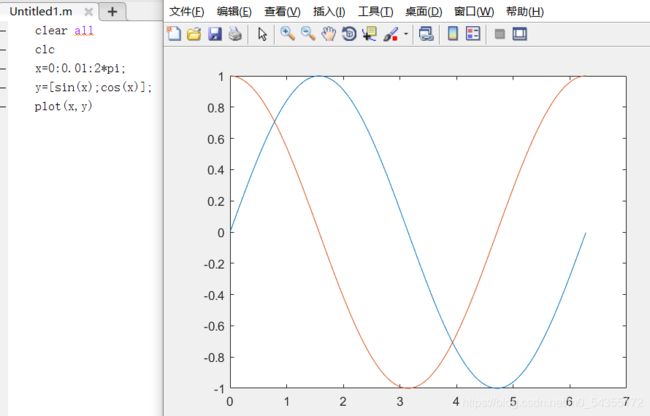
- 如果 X 是向量,而 Y 是一个矩阵,X 的长度与矩阵 Y 的行数或列数相等,则它的作用是将向量 X 与矩阵 Y 的每列或每行的向量相对应作折( 曲)线,当 Y 是方阵时,则将向量 X 与矩阵 Y 的列向量对应作图
- 如果 X 是矩阵,Y 是向量,Y 的长度等于矩阵 X 的行数或列数,则将 X 的每列或每行的向量与 Y 相对应作图。当 X 是方阵时,则将 X 的各列与 Y 对应作图
- 如果 X 和 Y 都是矩阵,且维数相同,则按列与列的对应方式来作图。
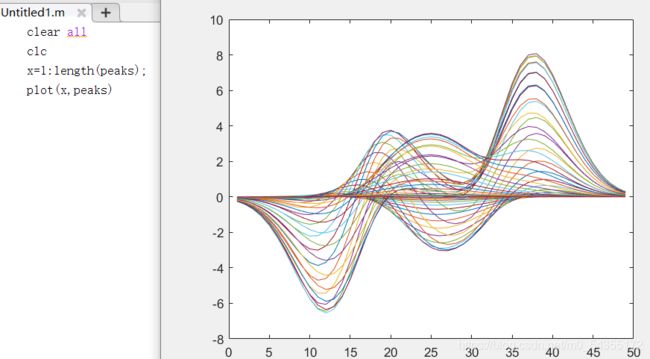
2.1.3.plot(Z)绘图
2.1.4.对数坐标曲线命令
semilogx:横坐标为对数坐标
semilogy:纵坐标为对数坐标
loglog:横纵坐标均为对数坐标
clear all
clc
t=0.1:0.1:3*pi;
y=sin(t)+1;
figure(1) %创建一个新的窗口
semilogx(t,y)
grid on %打开网格
figure(2)
semilogy(t,y)
figure(3)
loglog(t,y)
2.1.5.双y轴图形
绘制左右均有y轴的图形
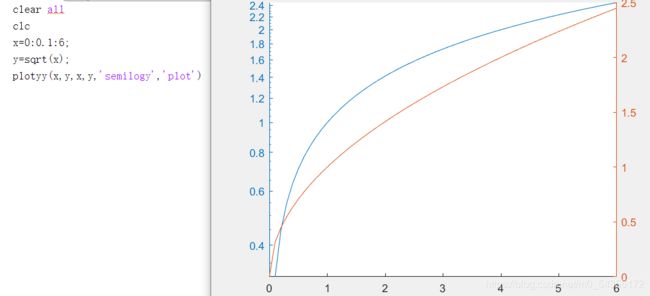
plotyy(x1,y1,x2,y2):在窗口中同时绘制两条曲线:(x1,y1)和(x2,y2),曲线(x1,y1)用左侧的 y 轴,曲线(x2,y2)用右侧的 y 轴
plotyy(x1,y1,x2,y2, 'fun'):'fun’是字符串,用来指定绘图的函数名,如 plot、semilogx、semilogy 等
plotyy(z1,y1,x2,y2, ‘fun1’, ‘fun2’):'fun1’和’fun2’指定不同的绘图函数分别绘制
注意: plotyy 函数不能加入设置曲线线型、颜色及标出数据点的参数
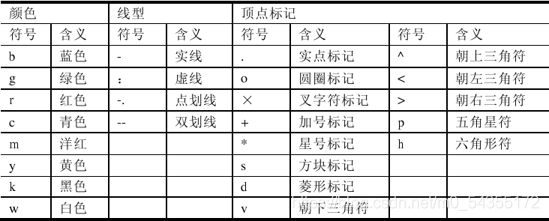
2.2.线型和颜色
调用格式
plot(x,y,s):s 为类型说明参数,是字符串
- s 字符串可以是三种类型的符号之一,也可以是线型与颜色和定点标记与颜色的组合
- 如果没有 s 参数,plot 将使用缺省设置(实线,前七种颜色顺序着色)绘制曲线
- 在当前坐标系中绘图时,每调用一次绘图函数,MATLAB将擦掉坐标系中已有的图形对象。可以用
hold on命令在一个坐标系中增加新的图形对象
注意: MATLAB会根据新图形的大小,重新改变坐标系的比例
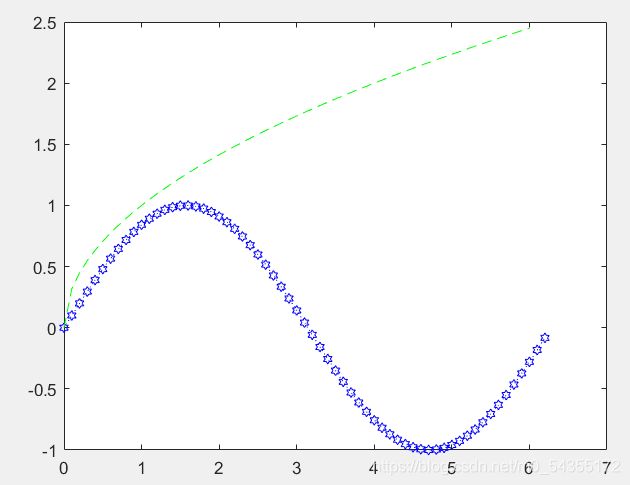
clear all
clc
t1=0:0.1:2*pi;
t2=0:0.1:6;
y1=sin(t1);
y2=sqrt(t2);
plot(t1,y1,':hb',t2,y2,'--g')
2.3.图形窗口的分割
subplot:实现在同一个窗口中同时显示多个图像的命令
subplot(m,n,i):把图形窗口分割为 m 行 n 列子窗口,然后选定第 i 个窗口为当前窗口
- subplot 命令不仅用于二维图形,对三维图形一样适用
- 其本质是将 figure 窗口分为几个区域,再在每个区域内分别绘图
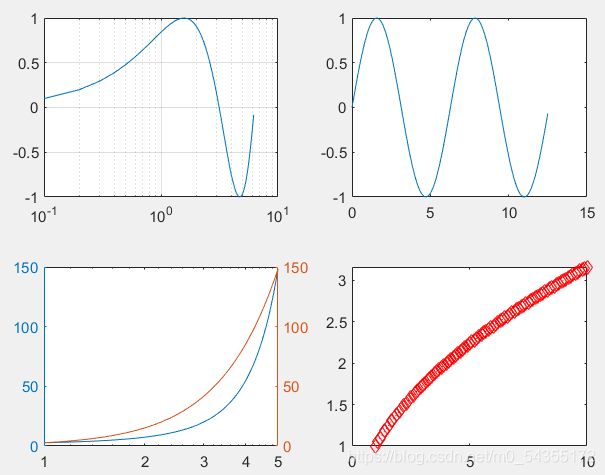
clear all
clc
%在第一个子窗口绘图
subplot(2,2,1)
t=0.1:0.1:2*pi;
y=sin(t);
semilogx(t,y)
grid on
%在第二个子窗口绘图
subplot(2,2,2)
t=0:0.1:4*pi;
y=sin(t);
plot(t,y)
%在第三个子窗口绘图
subplot(2,2,3)
x=1:0.01:5; y=exp(x);
plotyy(x,y,x,y,'semilogx','plot')
%在第四个子窗口绘图
subplot(2,2,4)
x=1:0.1:10; y=sqrt(x);
plot(x,y,':rd')
2.4.坐标系的调整
格式:axis([xmin,xmax,ymin,ymax,zmin,zmax])
坐标的最小值( xmin,ymin,zmin)必须小于相应的最大值( xmax,ymax,zmax),否则会出错
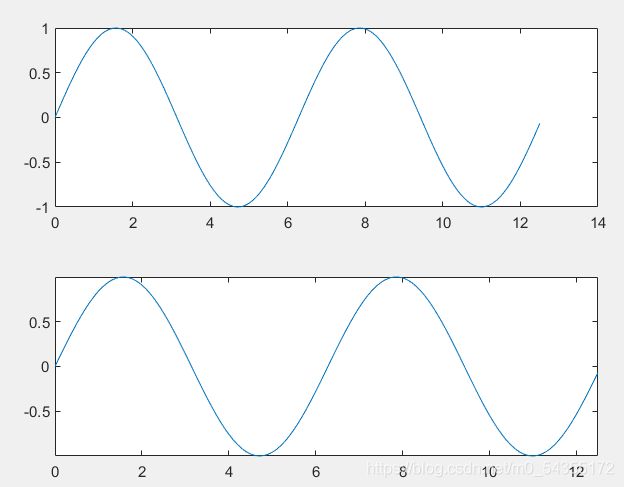
clear all
clc
%第一个图,未调整坐标系
subplot(2,1,1)
t=0:0.1:4*pi;
y=sin(t);
plot(t,y)
%第二个图,调整坐标系
subplot(2,1,2)
t=0:0.1:4*pi;
y=sin(t);
plot(t,y)
axis([0,max(t),min(y),max(y)])
3.三维绘图
3.1.三维曲线绘图指令
plot3:用来表现单参数的三维曲线
调用格式:
plot3(X1,Y1,Z1,s1,X2,Y2,Z2,s2,…)或plot3(X,Y,Z,s)
- Xn、Yn、Zn:第一到三维数据,是尺寸相等的向量/矩阵
1.1. X、Y、Z 是向量时,绘制以向量 X、Y、Z 的元素为 x、y、z 坐标的三维曲线
1.2.X、Y、Z 是矩阵时,以 X、Y、Z 对应列元素为 x、y、z 坐标分别绘制曲线- s、s1、s2:是字符串,用来设置线型、颜色、数据点标记
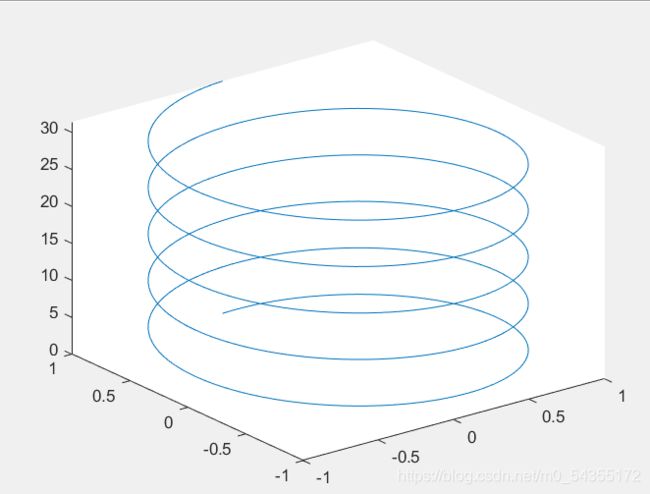
clear all
clc
t = 0:pi/50:10*pi;
st = sin(t);
ct = cos(t);
plot3(st,ct,t)
3.2.三维曲面绘图指令
绘制定义在平面区域 D =[x0,xm]×[y0,yn ]上的三维曲面z=f(x,y)
[x0,xm]在 x 方向分成 m 份,将[y0,yn]在 y 方向分成 n 份,由各划点分别作平行于坐标轴的直线,将区域 D 分成 m×n 个小矩形;对于每个小矩形,计算出网格点的函数值,决定出空间中四个顶点( xi,yi,f(xi,yi)),连接四个顶点得到一个空间的四边形片;所有四边形片连在一起构成函数 z=f(x,y)定义在区域 D 上的空间网格曲面
三维曲面绘图命令可分为平面网格点的生成、在平面网格基础上绘制三维网格及对三维表面进行处理三个步骤
3.2.1.平面网格点的生成
meshgrid:生成 x-y 平面上的网格点矩阵( 将由两个向量决定的区域转换为对应的网格点矩阵)
生成size(y)*size(x)的矩阵,相当于x从一行重复增加到size(y)行,把y转置成一列再重复增加到size(x)列
[X,Y]=meshgrid(x,y),[X,Y]=meshgrid(x)/[X,Y]=meshgrid(x,x)
- x:区间[x0,xm]上分划的向量
- y:区间[y0,yn]上分划的向量
- X,Y:输出变量矩阵,矩阵 X 的行向量都是向量 x,矩阵 Y 的列向量都是向量 y
[X,Y] = meshgrid(-2:2:2, -2:2:2)
Z = X.*exp(-X.^2 - Y.^2)
3.2.2.三维网格命令mesh
mesh:生成网格曲面
调用格式
| 格式 | 说明 |
|---|---|
| mesh(X,Y,Z,C) | X、Y、Z、C 是同维数的矩阵,X、Y、Z 对应空间上的网格点,网格线颜色由C决定 |
| mesh(X,Y,Z) | 相当于上面的 C=Z 的情况 |
| mesh(x,y,Z,C) | x 和 y 是向量,Z 和 C 是同维数的矩阵,网格曲面的网格顶点是( x(j),y(i),Z(i,j)),网格线的颜色由矩阵 C 决定 |
| mesh(x,y,Z) | 相当于上面的 C=Z 的情况 |
| mesh(Z,C) | 等价于 mesh(x,y,Z,C),此时向量x=1:n,向量 y=1:m |
| mesh(Z) | 相当于上面的 C=Z 的情况 |
| mesh(…,’PropertyName’,PropertyValue,…) | 给函mesh设置曲面属性 |
clear all
clc
[X,Y] = meshgrid(-2:0.2:2, -2:0.2:2);
Z = X.*exp(-X.^2 - Y.^2);
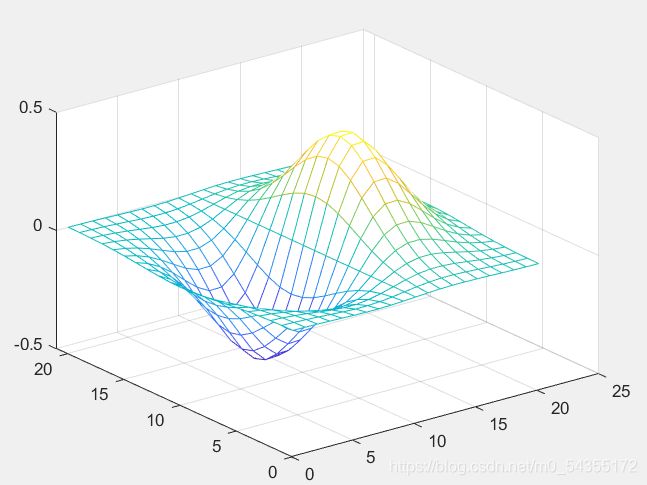
mesh(Z)
x = -7:0.2:7;
y = -7:0.2:7;
[X,Y] = meshgrid(x);
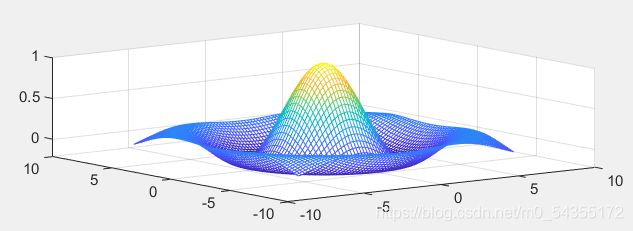
z = sin(sqrt(X.^2 + Y.^2))./(sqrt(X.^2 + Y.^2));
subplot(2,1,1)
mesh(X,Y,z)
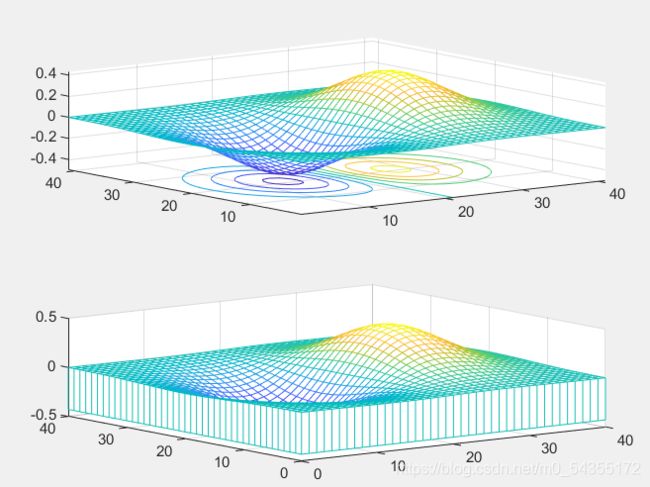
3.2.3.三维网格命令meshc、meshz
meshc:除生成网格曲面外,还在 x-y 平面上生成曲面的等高线图形
meshz:除生成与 mesh 相同的网格曲面外,还在曲面下面加上一个长方体的台柱
clear all
clc
[X,Y] = meshgrid(-2:0.1:2, -2:0.1:2);
Z = X.*exp(-X.^2 - Y.^2);
subplot(2,1,1)
meshc(Z)
subplot(2,1,2)
meshz(Z)
3.2.4.三维表面命令surf
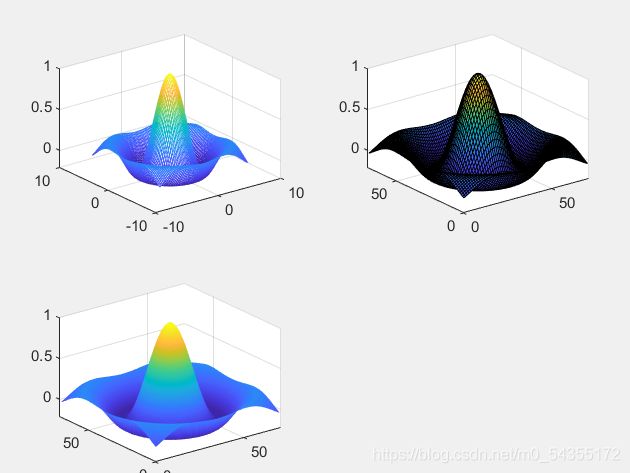
surf:实现对网格曲面片进行着色,将网格曲面转化为实曲面(surf 命令的调用格式与 mesh 相同)
shading interp:平滑处理
x = -7:0.2:7;
y = -7:0.2:7;
[X,Y] = meshgrid(x);
z = sin(sqrt(X.^2 + Y.^2))./(sqrt(X.^2 + Y.^2));
subplot(2,2,1)
mesh(X,Y,z)
subplot(2,2,2)
surf(z)
subplot(2,2,3)
surf(z)
shading interp
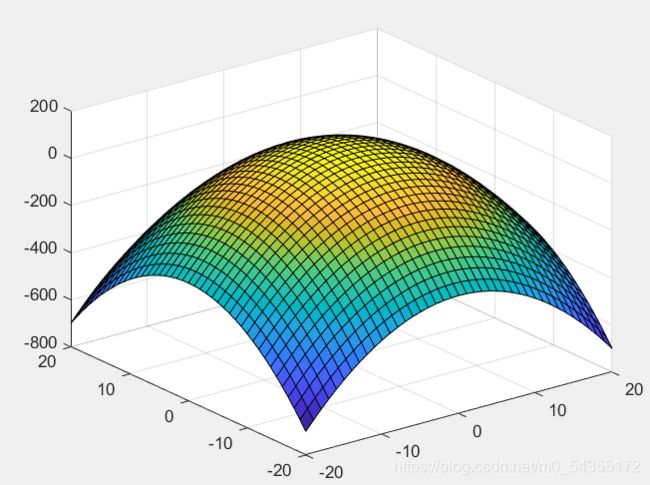
clear all
clc
x=-20:1:20;
y=-20:1:20;
[X,Y]=meshgrid(x,y);
z=-X.^2-Y.^2+100;
surf(X,Y,z)
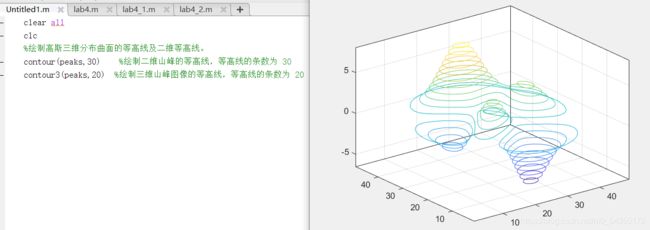
3.2.5.等高线图形的绘制
counter:绘制出二维图形的等高线
contour3:绘制出三维图形的等高线
| 指令 | 说明 |
|---|---|
| contour(Z) | 直接绘制矩阵 Z 的等高线 |
| contour(X,Y,Z) | 用 X 和 Y 指定等高线的 x、y 坐标 |
| contour(Z,n) contour(X,Y,Z,n) |
绘制 n 条等高线 |
| contour(Z,V) contour(X,Y,Z,V) |
向量 V 的元素指定等高线的位置,该向量长度 length(V)对应绘制的等高线条数 |
3.2.6.柱面和球面的三维表达
cylinder:柱面表达式(柱面的轴线定义为 z 轴,只要给出母线的描述就可完成一个柱面)
调用格式:
[X,Y,Z] = cylinder(R,N)[X,Y,Z] = cylinder(R):缺省值 N=20[X,Y,Z] = cylinder:缺省值 N=20,R=[1,1]
R:是一描述柱面母线的向量;
N:是旋转柱面上的分割线条数;
[X,Y,Z] :是返回的x,y,z坐标向量
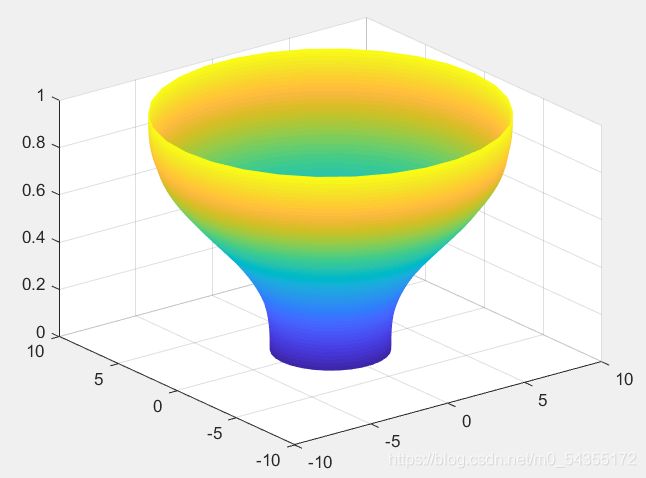
clear all
clc
t=pi:0.01:3*pi;
r=sin(t)+t;
cylinder(r,30)
shading interp %平滑处理
sphere:球面的表达式
调用格式:
[X,Y,Z]=sphere(N):产生一个( N+1)×( N+1)的矩阵,然后用函数 surf 命令绘制一个单位的球面,N 为设置分割线的条数[X,Y,Z] = sphere:缺省值 N = 20
4.特殊图形绘制
4.1.直方图命令 bar
bar、bar3:直方图常用于统计数据的作图(两指令调用格式类似)
调用格式:
1.bar(X,Y):X 是横坐标向量,Y 可以是向量或矩阵。Y 是向量时,每一个元素对应一个竖条;Y 是 m 行 n 列矩阵时,将画出 m 组竖条,每组包括 n 个竖条
2.bar(Y):横坐标使用缺省值 X=1:M
3.bar(X,Y,WIDTH)、bar(Y,WIDTH):用 WIDTH 指定竖条的宽度,如果 WIDTH>1,条与条之间将重合。缺省宽度为 0.8
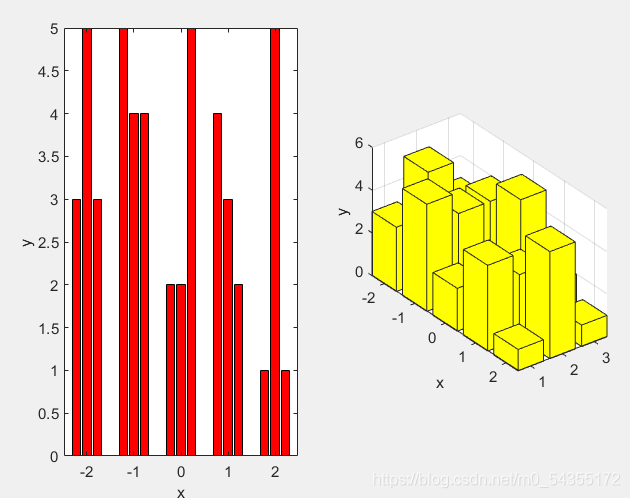
clear all
clc
X=-2:2;
Y=[3,5,2,4,1;5,4,2,3,5;3,4,5,2,1];
subplot(1,2,1)
bar(X,Y','r')
xlabel('x')
ylabel('y')
subplot(1,2,2)
bar3(X,Y','y')
zlabel('y')
ylabel('x')
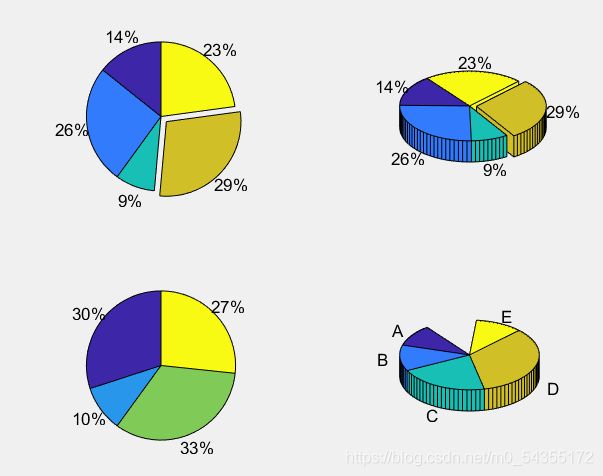
4.2.饼图命令 pie
pie 、 pie3:饼图又叫扇形图,用于显示向量中元素所占向量元素总和的百分比(两指令调用格式类似)
调用格式:
pie(X):向量 X 的饼图。把 X 的每一个元素在所有元素总和中占的比例表达出来pie(X,Y):向量Y(和向量X长度相等)用于指定饼图中抽出一部分的块(非零值对应的块)pie(...,LABELS):LABELS 是用于标注饼图的字符串数组细胞,其长度必须和向量 X相等H = pie(...):返回包括饼图和文本对象句柄
clear all
clc
x=[200,360,120,400,320];
subplot(2,2,1),
pie(x,[0 0 0 1 0])
subplot(2,2,2),
pie3(x,[0 0 0 1 0])
subplot(2,2,3),
pie(x(2:5))
subplot(2,2,4),
x=[0.1,0.12,0.21,0.34,0.11];
pie3(x ,{'A','B','C','D','E'})
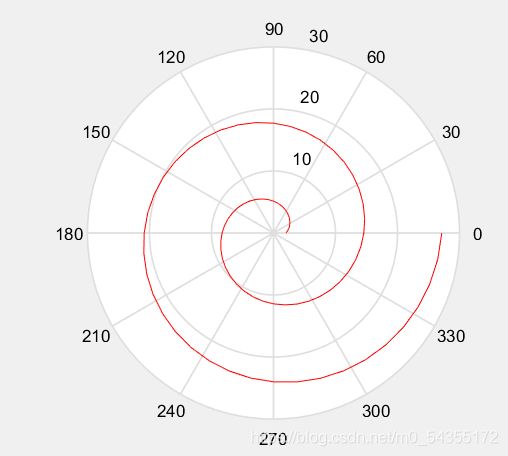
5.极坐标系下绘制图形
polar:直接在极坐标系下绘图的命令
polar(THETA, RHO,S):按照坐标的角度theta,半径rho绘制图形,S 是字符串,用来控制图形的线型
clear all
clc
rhe=2;
theta=0:pi/20:4*pi;
rho=rhe+theta*rhe;
polar(theta,rho,'r')
6.坐标轴的调整和图形的标注
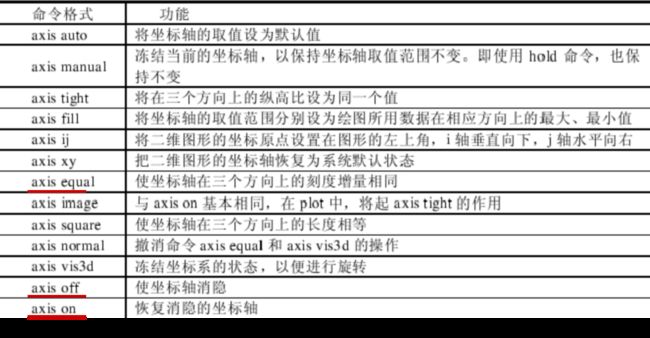
6.1.坐标轴调整命令
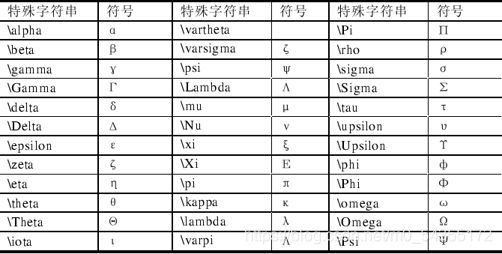
6.2.特征字符串中的希腊字母
6.3.特征字符串中的其他字符
6.4.图例的标注
6.4.1.图例的说明legend
legend:实现不同图例的说明
调用格式:
legend(string1,string2,string3, ...)、legend(string1,string2,string3,...,’Location’,’Pos’):按顺序把字符串添加到相应的曲线线型符号之后Pos:NorthEast 图窗右上角(默认)、NorthWest 图窗左上角、SouthEast 图窗右下角、SouthWest 图窗左下角
clear all
clc
a=rand(10,10);
surf(a)
xlabel('x');
ylabel('y');
zlabel('z');
title('三维曲面')
legend('曲面','location','northwest')
6.4.2.控制分格线grid
grid on:打开分格线控制开关,以后绘制的图形都带有分格线
grid off:关闭分格线控制开关,以后绘制的图形都不带分格线
grid:用于实现分格线绘制切换
6.4.3.标记函数text
text(x,y,'text'):图形窗口的(x,y)处写字符串’text’
6.4.4.设置坐标轴set
set(gca,’属性’,value)
clear all
clc
x = linspace(0,10);
y = sin(4*x);
plot(x,y)
set(gca,'fontsize',16,'fontname','times New Roman');
set(gca,'ylim',[-2,2])
set(gca,'xlim',[1,5])
6.4.5.使用函数 xlabel、title 和 legend 命令进行标注
clear all
clc
t=0:0.1:4*pi;
y=sin(t);
y1=cos(t);
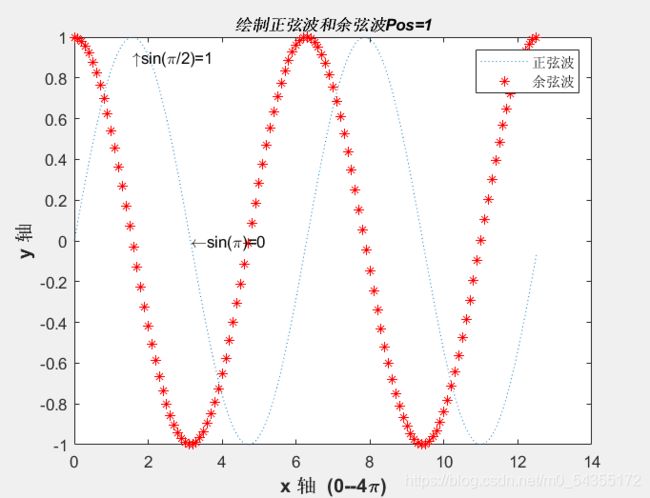
plot(t,y,':',t,y1,'r*')
xlabel('x 轴 (0--4\pi)','fontsize',12,'fontweight','bold')
ylabel('y 轴','fontsize',12,'fontweight','bold')
title('绘制正弦波和余弦波Pos=1','fontsize',10,'fontweight','bold','fontangle','italic')
text(pi,0,'\leftarrowsin(\pi)=0')
text(pi/2,0.9,['\uparrowsin(\pi/2)=',num2str(sin(pi/2))])
legend('正弦波','余弦波')