KMP --算法竞赛（33）

前驱教材：《算法竞赛入门到进阶》 清华大学出版社
网购：京东 当当   作者签名书：点我
有建议请加QQ 群：567554289

本系列文章将于2021年整理出版。最近忙着赶稿，有一个多月没有发专题了。今天发一篇。一个多月后基本搞完初稿，再多发一些。

   KMP是字符串模式匹配算法，它包括预处理模式串和匹配两部分，复杂度为O(m + n)，是此类算法能达到的最优复杂度。KMP的思路和编码很巧妙。

1. 朴素的模式匹配算法

  模式匹配（Pattern Matching）问题：在一篇长度为$n$的文本$S$中，找某个长度为$m$的关键词$P$。$P$可能多次出现，都需要找到。
  最优的模式匹配算法复杂度能达到多好？由于至少需要检索文本$S$的$n$个字符和关键词$P$的$m$个字符，所以复杂度至少是$O(m+n)$。
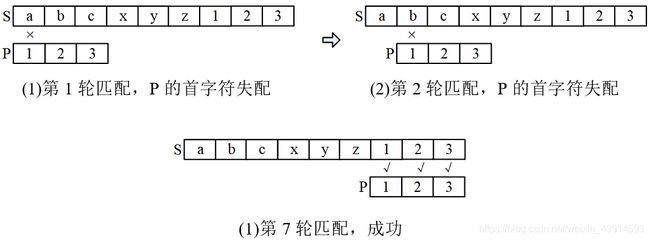
  先考虑朴素的模式匹配算法（暴力方法）：从$S$的第一个字符开始，逐个匹配$P$的每个字符。例如$S=“abcxyz123”，P=“123”$。第1轮匹配，$P[0]\ne S[0]$，称为“失配”，后面的$P[1]、P[2]$不用再比较。一共比较6 + 3 = 9次：前6轮比较$P$的第1个字符，第7轮比较$P$的3个字符 。
  (把P看成一个滑块，在轨道S上滑动，直到匹配。)

图1 朴素的模式匹配算法例1

  这个例子比较特殊，$P$和$S$的字符基本都不一样。在每轮匹配时，往往第1个字符就对不上，用不着继续匹配$P$后面的字符。复杂度差不多是$O(n)$，这已经是字符串匹配能达到的最优复杂度了。所以，如果字符串$S、P$符合这个特征，暴力法是不错的选择。

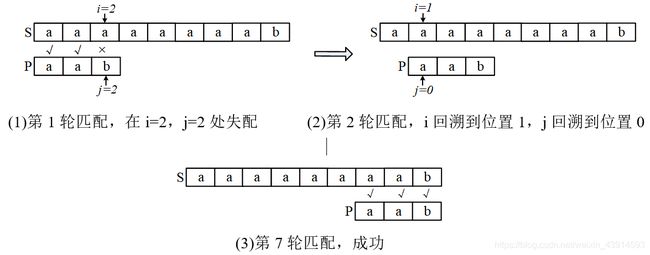
  但是如果情况很坏，例如$P$的前$m-1$个都容易找到匹配，只有最后一个不匹配，那么复杂度就退化成$O(nm)$。例如$S=“aaaaaaaab”，P=“aab”$。图2中$i$指向$S[i]$，$j$指向$P[j]，0\le i<n，0\le j<m$。第1轮匹配后，在$i=2，j=2$的位置失配。第2轮让$i$回溯到1，$j$回溯到0，重新开始匹配。最后经过7轮，共匹配7×3 = 21次，远远超过上面例子中的9次。

图2 朴素的模式匹配算法例2

2. KMP算法

  KMP是一种在任何情况下都能达到$O(n+m)$复杂度的算法。它是如何做到的？用KMP算法时，指向$S$的$i$指针不会回溯，而是一直往后走到底。与朴素方法比较，大大加快了匹配速度。

  在朴素方法中，每次新的匹配都需要对比$S$和$P$的全部$m$个字符，这实际上做了重复操作。例如第一轮匹配$S$的前3个字符$“aaa”$和$P$的$“aab”$，第二轮从$S$的第2个字符$‘a’$开始，与和$P$的第一个字符$‘a’$比较，这其实不必要，因为在第一轮比较时已经检查过这两个字符，知道它们相同。如果能记住每次的比较，用于指导下一次比较，使得$S$的$i$指针不用回溯，就能提高效率。
  如何让$i$不回溯？分析两种情况。

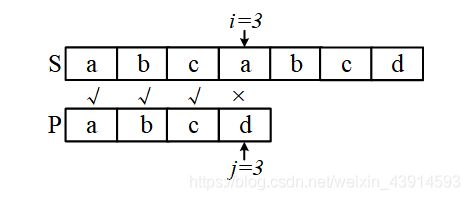
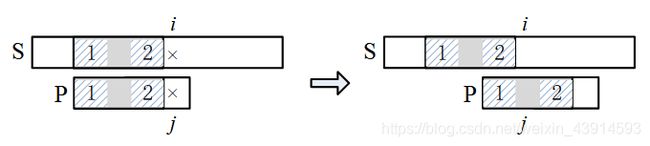
（1）P在失配点之前的每个字符都不同
  例如$S=“abcabcd”，P=“abcd”$，第一次匹配的失配点是$i=3，j=3$。失配点之前的$P$的每个字符都不同，$P[0]\ne P[1]\ne P[2]$；而失配点之前的$S$与$P$相同，即$P[0]=S[0]、P[1]=S[1]、P[2]=S[2]$。下一步如果按朴素方法，$j$要回到位置0，$i$要回到1，去比较$P[0]$和$S[1]$。但$i$的回溯是不必要的。由$P[0]\ne P[1]、P[1]=S[1]$推出$P[0]\ne S[1]$，所以$i$没有必要回到位置1。同理，$P[0]\ne S[2]$，$i$也没有必要回溯到位置2。所以i不用回溯，继续从$i=3、j=0$开始下一轮的匹配。

图3 失配点之前的P的每个字符都不同

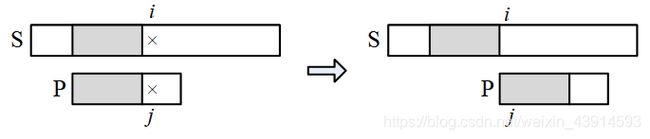
  下面画出示意图。当$P$滑动到左图位置时，$i$和$j$所处的位置是失配点，$S$与$P$的阴影部分相同，且阴影内部的$P$的字符都不同。下一步直接把$P$滑到$S$的$i$位置，此时$i$不变、$j$回到0，然后开始下一轮的匹配。

图4 P的每个字符都不同的滑动情况

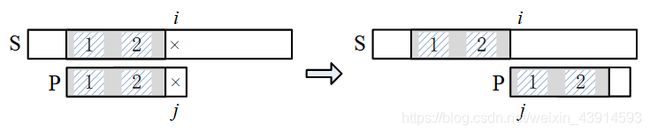
（2）P在失配点之前的字符有部分相同
  再细分两种情况：

  1）相同的部分是前缀（位于$P$的最前面）和后缀（位于$j$的前面）。
  这里给出前缀和后缀的定义：字符串$A$和$B$，若存在$A=BC$，其中$C$是任意的非空字符串，称$B$为$A$的前缀；同理可定义后缀，若存在$A=CB$， $C$是任意非空字符串，称$B$为$A$的后缀。从定义可知，一个字符串的前缀和后缀不包括自己。
  当$P$滑动到下面左图位置时，$i$和$j$所处的位置是失配点，$j$之前的部分与$S$匹配，且子串1（前缀）和子串2（后缀）相同，设子串长度为$L$。下一步把$P$滑到右图位置，让$P$的子串1和$S$的子串2对齐，此时$i$不变、$j=L$，然后开始下一轮的匹配。注意，前缀和后缀可以部分重合。

图5 相同的部分是前缀和后缀

  2）相同部分不是前缀或后缀。
  下面左图，$P$滑动到失配点$i$和$j$，前面的阴影部分是匹配的，且子串1和2相同，但是1不是前缀（或者2不是后缀），这种情况与“（1）失配点之前的P的每个字符都不同”类似，下一步滑动到右图位置，即$i$不变，$j$回溯到0。请读者自己分析。

图6 相同的部分不是前缀或后缀

  通过上面的分析可知，不回溯$i$完全可行。KMP算法的关键在于模式$P$的前缀和后缀，计算每个$P[j]$的前缀、后缀，记录在$Next[]$数组（也有写成$shift$或者$fail$的）中，$Next[j]$的值等于$P[0]-P[j-1]$这部分子串的前缀集合和后缀集合的交集的最长元素的长度。把这个最长元素称为“最长公共前后缀”。

  例如$P=“abcaab”$，计算过程如下表，每一行的红色带下划线的子串是最长公共前后缀。

图7 最长公共前后缀

  $Next[]$只和$P$有关，通过预处理$P$得到。下面介绍一种复杂度只有$O(m)$的极快的方法，它巧妙地利用了前缀和后缀的关系，从$Next[i]$递推到$Next[i+1]$。
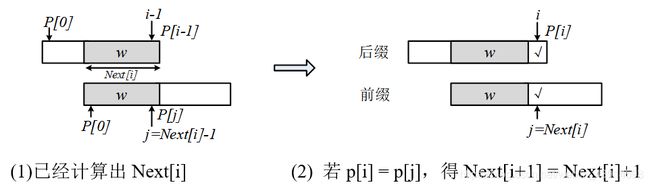
  假设已经计算出了$Next[i]$，它对应$P[0]-P[i-1]$这部分子串的后缀和前缀，见下面图8(1)所示。后缀的最后一个字符是$P[i-1]$。阴影部分$w$是最长交集，交集$w$的长度为$Next[i]$，这个交集必须包括后缀的最后一个字符$P[i-1]$和前缀的第一个字符$P[0]$。前缀中阴影的最后一个字符是$P[j]，j=Next[i]-1$。

  图8(2)推广到求$Next[i+1]$，它对应$P[0]P[i]$的后缀和前缀。此时后缀的最后一个字符是$P[i]$，与这个字符相对应，把前缀的$j$也往后移一个字符，$j=Next[i]$。判断两种情况：
  （1）若$P[i]=P[j]$，则新的交集等于“阴影$w+P[i]$”，交集的长度$Next[i+1]=Next[i]+1$。如图(2)所示。

图8 若p[i] = p[j]，从Next[i]推广到Next[i+1]

  （2）若$P[i]\ne P[j]$，说明后缀的“阴影$w+P[i]$”与前缀的“阴影$w+P[j]$”不匹配，只能缩小范围找新的交集。把前缀往后滑动，也就是通过减小j来缩小前缀的范围，直到找到一个匹配的$P[i]=P[j]$为止。如何减小$j$？只能在$w$上继续找最大交集，这个新的最大交集是$Next[j]$，所以更新$j’=Next[j]$。下图(2)画出了完整的子串$P[0]P[i]$，最后的字符$P[i]$和$P[j]$不等。斜线阴影$v$是$w$上的最大交集，下一步判断：若$P[i]=P[j’]$，则$Next[i+1]$等于$v$的长度加1，即$Next[j’]+1$；若$P[i]\ne P[j’]$，继续更新$j’$。

图9 若p[i] ≠ p[j]，更新j’ = Next[j]

  重复以上操作，逐步扩展$i$，直到求得所有的$Next[i]$。

3. 模板代码

  用下面的例题hdu 2087给出模板代码，包括$getNext()、kmp()$两个函数。$getNext()$预计算$Next[]$数组，是前面图解思路的完全实现，请对照注释学习这种巧妙的方法。$kmp()$函数在$S$中匹配所有的$P$，注意每次匹配到的起始位置是$s[i+1-plen]$，末尾是$s[i]$。
  KMP算法的复杂度：$getNext()$函数的复杂度为$O(m)$；匹配函数$kmp()$从$S[0]$到$S[n-1]$只走了一遍，$S$的每个字符只与$P$的某个字符比较了1次，复杂度为$O(n)$；总复杂度为$O(n+m)$。

---

剪花布条 hdu 2087
题目描述：一块花布条，上面印有一些图案，另有一块直接可用的小饰条，也印有一些图案。对于给定的花布条和小饰条，计算一下能从花布条中尽可能剪出几块小饰条。
输入：每一行是成对出现的花布条和小饰条。#表示结束。
输出：输出能从花纹布中剪出的最多小饰条个数。
Sample Input：
abcde a3
aaaaaa aa

Sample Output：
0
3

---

  本题代码套用了KMP的模板。找到的$P$有很多个，而且可能重合，例如$“aaaaaa”$包含了5个$“aa”$。但在本题中，需要找到能分开的子串，即剪出不同的小饰条。这个问题容易解决，只需要在程序中加一句$if(i-last>=plen)$进行判断即可。

#include
using namespace std;
const int N = 1005;
char str[N], pattern[N];
int Next[N];
int cnt;
void getNext(char *p, int plen){
      //计算Next[1]~Next[plen]
    Next[0]=0; Next[1]=0;
    for(int i=1; i < plen; i++){
       //把i的增加看成后缀的逐步扩展
        int j = Next[i];          //j的后移：j指向前缀阴影w的后一个字符
        while(j && p[i] != p[j])  //阴影的后一个字符不相同
            j = Next[j];          //更新j
        if(p[i]==p[j])   Next[i+1] = j+1;
        else             Next[i+1] = 0;
    }
}
int kmp(char *s, char *p) {
              //在s中找p
    int last = -1;
    int slen=strlen(s), plen=strlen(p);
    getNext(p, plen);               //预计算Next[]数组
    int j=0;
    for(int i=0; i<slen; i++) {
          //匹配S和P的每个字符
        while(j && s[i]!=p[j])      //失配了。注意j==0是情况(1)
             j=Next[j];             //j滑动到Next[j]位置
        if(s[i]==p[j])  j++;        //当前位置的字符匹配，继续
        if(j == plen) {
                  //j到了P的末尾，找到了一个匹配
           	//这个匹配，在S中的起点是i+1-plen，末尾是i。如有需要可以打印：
           	// printf("at location=%d, %s\n", i+1-plen,&s[i+1-plen]);
            //-------------------30--33行是本题相关
            if( i-last >= plen) {
        //判断新的匹配和上一个匹配是否能分开
                cnt++;
                last=i;              //last指向上一次匹配的末尾位置
            }
            //-------------------
        }
    }
}
int main(){
     
    while(~scanf("%s", str)){
           //读串
        if(str[0] == '#')  break;
        scanf("%s", pattern);      //读模式串
        cnt = 0;
        kmp(str, pattern);
        printf("%d\n", cnt);
    }
    return 0;
}

4. 例题

4.1 最短循环节问题

---

洛谷 P4391
题目描述：字符串$S1$由某个字符串$S2$不断自我连接形成，但是字符串$S2$未知。给出$S1$的一个长度为$n$的片段$S$，问可能的$S2$的最短长度是多少。例如给出$S1$的一个长度为8的片段$P=“cabcabca”$，求最短的$S2$长度，答案是3，$S2$可能是$“abc”、“cab”、“bca”$等。

---

题解：求字符串$P$的最短循环节，读者可能想不到和最长公共前后缀、KMP的$Next[]$数组有关。下面讨论两种情况，请读者自己画图帮助理解。
  1）$P$由完整的$k$个$S2$连接而成。则$Next[n]$等于$k-1$个$S2$的长度，那么剩下的$n-Next[n]$等于一个$S2$的长度。
  2）$P$由$k$个完整的$S2$和1个不完整的$S2$连接而成。设$S2$长度为$L$，不完整的部分长度为$Z$。则$Next[n]=(k-1)L+Z，n-Next[n]=kL+Z-(k-1)L-Z=L$就是答案。
  综合起来答案等于$n-Next[n]$。本题例子$“cabcabca”，n=8，Next[n]=5$，最长公共前后缀是$“cabca”$，答案是$n-Next[n]=3$。
  这一题可以帮助深入理解最长公共前后缀和$Next[]$数组。

4.2 在S中删除所有的P

---

洛谷 P4824
题目描述：给定一个字符串$S$和一个子串$P$，删除$S$中第一次出现的$P$，把剩下的拼在一起，然后继续删除$P$，直到$S$中没有$P$，最后输出$S$剩下的部分。$S$中最多有$10^6$个字符。
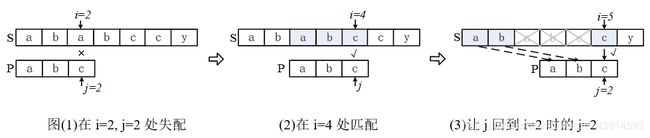
  本题的麻烦之处在于，删除一个$P$之后两端的字符串有可能会拼接出一个新的$P$。例如$S=“ababccy”，P=“abc”$，删除第一个$P$后，$S=“abcy”$，出现了一个新的$P$，继续删除，得$S=“y”$。

---

题解：在$S$中找$P$是典型的KMP算法。不过，如果每找到并删除一个$P$后，就重组$S$然后在新的$S$上再做一次KMP，会超时。能不能在删除一个$P$后，继续在原$S$上匹配和删除，总共只做一次KMP？
  如果对KMP算法中$i、j$指针的移动有深刻理解，本题的任务是能用一次KMP完成的。如图10所示，图(1)在$i=2，j=2$处失配。图(2)找到了一个匹配，$i=4$，在正常情况下，$j$应该回到0开始下一轮的匹配，但是这里让$j$回到被删除的$P$前面的值，即$i=2$时的$j=2$，然后直接与$i=5$对比，这样就衔接上了被删除的$P$前后的字符串。在这个过程中$S$不用重组，$i$不用回溯，一共只做了一次KMP。

图10 删除P后衔接前后的字符

  编码时在正常KMP中加入两条：
  1）定义一个和$S$一样大的数组记录每个字符对应的$j$值，用于删除一个$P$后$j$回到P前面的值。
  2）用一个栈记录删除$P$后的结果。每移动一次$i$就把$S[i]$进栈，若KMP匹配到一个$P$，此时栈顶就是$P$，把栈顶的$P$弹出栈，相当于删除了这个$P$。最后栈中留下的就是$S$删除了所有$P$的结果。

【习题】

Hdu：1686，1711，2222，2896，3065，3336，2594。
POJ：1961，2406。
洛谷：P3375，P3435，P2375，P3426，P3193。