排序算法 - 快速排序

简介

同冒泡排序一样，快速排序也属于交换排序，通过元素之间的比较和 交换位置来达到排序的目的。

不同的是，冒泡排序在每一轮中只把1个元素冒泡到数列的一端，而快速排序则在每一轮挑选一个基准元素，并让其他比它大的元素移动到数列一边，比它小的元素移动到数列的另一边，从而把数列拆分成两个部分。

• 紫色：基准元素
• 绿色：比基准元素大的元素
• 黄色：比基准元素小的元素

这种思路叫做分治法，假如给出如上图数组，一般情况下，使用冒泡排序需要比较七轮，每一轮把1个元素移动刀数列的一端，时间复杂度O(n^)。

基准元素的选择

基准元素，英文pivot ，在分治过程中，以基准元素位中心，把其他元素移动到它的两侧

1. 一般情况下最简单的方式是选择数列的第一个元素
2. 随机选择一个 元素作为基准元素，并且让基准元素和数列首元素交换位置

快速排序流程：

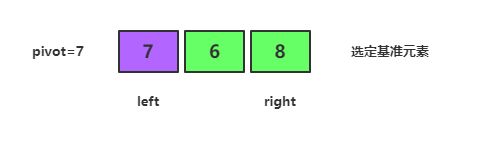
首先，选定基准元素 pivot ，并且设置 left 和 right 指针，指向左右两个元素

       

• 第一次循环

        right 指针开始，让指向的元素和基准元素做比较。如果大于或等于基准元素，则指针向左移动，如果小于基准元素，则 right 停止移动。当前数列 7 > 5 向左移动，1 < 5 停止移动,切换 left 指针。

        left 指针开始，让指向的元素和基准元素做比较。如果小于或等于基准元素，则指针向右移动，如果大于基准元素，则 left 指针停止移动， 8 > 5 停止移动

        当 right 和 left 都停止后，让 left 和 right 指针所指向的元素交换位置

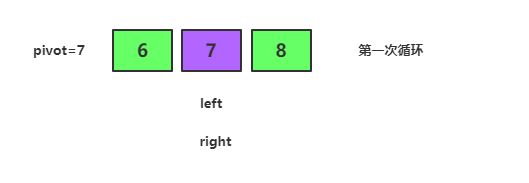
• 第二次循环

        切换到 right 指针，向左移动 right 先移动到 2， 2 < 5 停止移动

        切换到 left 指针，向右移动 left 移动到6 ，6 > 5 停止移动

• 第三次循环

        切换到 right 指针，向左移动 right 先移动到 9， 9 > 5 向左继续移动 right 移动到 3 ，3 < 5 停止移动

        切换到 left 指针，向右移动 left 移动到 3 ，和 right 重合，将 基准元素 5 和 重合元素 3 交换

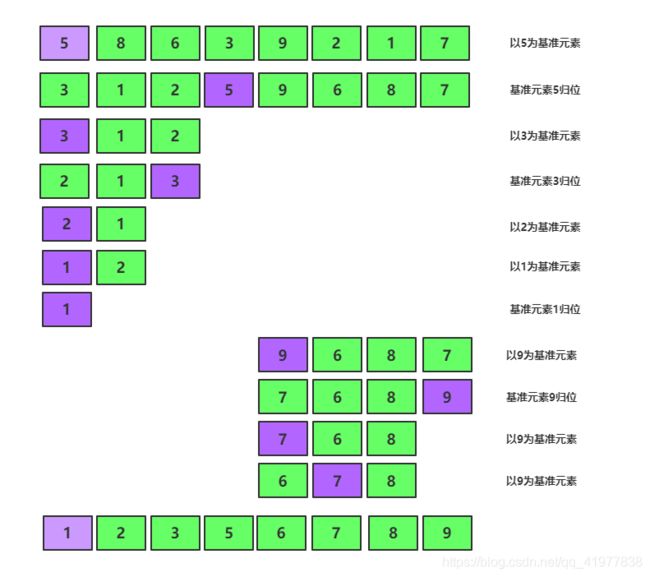
到此第一轮“探测”真正结束。此时以基准数 5 为分界点，5 左边的数都小于等于5，5 右边的数都大于等于5 。

现在 基准元素 5 已经归位 ， 此时我们以 5为分界点拆分成两个数列 ，左边的数列 [3，1,2] ，右边的数列 [9，6，8，7]，接下来还需要分别处理这两个数列

左边序列 ：

• 第一轮循环

        从 right 指针开始，2 < 3 停止移动

        切换到 left 指针，1 < 3 继续向右移动，left 和 right 重合，交换元素

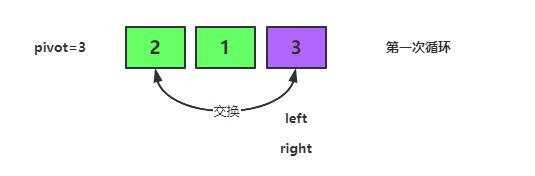
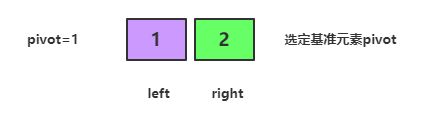
基准元素 3 已经归位，接下来需要处理 基准元素 3 左边的序列 [2，1]

右边序列 ：

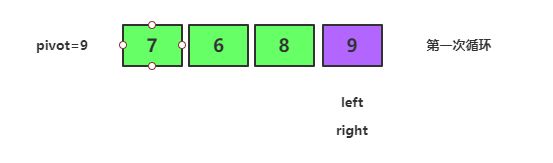
        从 right 指针开始，7 < 9 停止移动

        切换到 left 指针，6 < 9 继续向右移动，8 < 9 继续向右移动 与 right 指针重合，交换元素

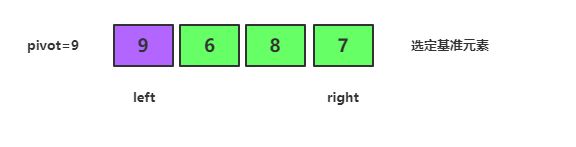
基准元素 9 已经归位，接下来需要处理 基准元素 9 左边的序列 [7，6，8]

最后得到的序列如下：[1，2，3，5，6，7，8]

在分治法的思想下，原数列在每一轮都被拆分成两部分，每一部分在下一轮又分别被拆分成两部分，直到不可再分为止。

算法处理过程：

代码 ：

/**
 * 快速排序
 */
public class demo3 {
     

    public static void main(String[] args) {
     
        int array[] = {
     5,8,6,3,9,2,1,7};
        quickSort(array,0,array.length-1);
        System.out.printf(Arrays.toString(array));
    }


    public static void quickSort(int[] arr,int startIndex,int endIndex){
     
        //递归结束
        if(startIndex >= endIndex){
     
            return;
        }
       //取第一个位置为基准元素
        int pivot = arr[startIndex];
        int left = startIndex;
        int right = endIndex;

        while (left != right){
     
            //控制right指针比较并且左移
            while (left < right && arr[right] > pivot){
     
                right--;
            }
            //控制left指针比较并且右移
            while (left < right && arr[left] <= pivot){
     
                left++;
            }
            if(left<right){
     
                int p = arr[left];
                arr[left] = arr[right];
                arr[right] = p;
            }

        }

        //pivot和指针重合点交换
        arr[startIndex] = arr[left];
        arr[left] = pivot;

        quickSort(arr,startIndex,right - 1);
        quickSort(arr,right + 1,endIndex);

    }


}

[1, 2, 3, 5, 6, 7, 8, 9]

个人博客地址：http://blog.yanxiaolong.cn ｜ 『纵有疾风起，人生不言弃』