图论(graph)相关算法总结
图论(graph)相关算法总结
文章目录
-
- 图论(graph)相关算法总结
-
- 1 图的典型应用
- 2 无向图
- 2.1 术语表
- 2.2 表示无向图的数据类型
- 2.3 图的几种表示方法
- 2.4 邻接表的数据结构
- 2.5 深度优先搜索(DFS)
- 2.6 广度优先搜索(BFS)
- 2.7 连通分量
- 2.8 无环图的判断
- 2.9 二分图的判断
- 3 有向图
- 3.1 有向图术语
- 3.2 有向图的数据类型
- 3.3 标记-清除的垃圾收集
- 3.4 寻找有向环
- 3.5 有向图基于DFS搜索的顶点排序
- 3.6 拓扑排序
- 3.7 有向图的强连通性
- 3.8 `Kosaraju`算法求强连通分量
1 图的典型应用
| 应用 | 结点 | 连接 |
|---|---|---|
| 地图 | 十字路口 | 公路 |
| 网络内容 | 网页 | 超链接 |
| 电路 | 元器件 | 导线 |
| 任务调度 | 任务 | 限制条件 |
| 商业交易 | 客户 | 交易 |
| 计算机网络 | 网站 | 物理连接 |
| 软件 | 方法 | 调用关系 |
| 社交网络 | 人 | 友谊关系 |
2 无向图
定义:
无向图是由一组顶点(vertex)和一组能够将两个顶点相连的边(edge)组成的。
特殊的图:我们的定义允许出现两种简单而特殊的情况
-
自环,即一条连接一个顶点和其自身的边 - 连接同一对顶点的两条边称为
平行边
数学家常常将含有平行边的图称为多重图,而将没有平行边或自环的图称为简单图。一般来说,允许出现自环和平行边。
2.1 术语表
当两个顶点通过一条边相连时,我们称这两个顶点是相邻的,并称这条边依附于这两个顶点。某个顶点的度数即为依附于它的边的总数。子图是由一幅图的所有边的一个子集(以及它们所依附的所有顶点)组成的图。
定义:在图中,
路径是由边顺序连接的一系列顶点。简单路径是一条没有重复顶点的路径。环是一条至少含有一条边且起点和终点相同的路径。简单环是一条(除了起点和终点必须相同之外)不含有重复顶点和边的环。路径或者边的长度为其中所包含的边数。
✨
定义:如果从任意一个顶点都存在一条路径到达另一个任意顶点,我们称这幅图是
连通图。一幅非连通的图由若干连通的部分组成,它们都是其极大连通子图
✨
定义:
树是一幅无环连通图。互不相连的树组成的集合称为森林。连通图的生成树是它的一幅子图,它含有图中的所有顶点且是一颗树。图的生成树森林是它的所有连通子图的生成树的集合。
✨
图的密度是指已经连接的顶点对所占可能被连接的顶点对的比例。在稀疏图中,被连接的顶点对很少;而在稠密图中,只有少部分顶点对之间没有边连接。
✨
二分图是一种能够将所有结点分为两部分的图,其中图的每条边所连接的两个顶点都分别属于不同的部分。
2.2 表示无向图的数据类型
无向图的API
public class Graph
---------------------------------------------------------------------------------
Graph(int V) 创建一个含有V个顶点但不含有边的图
Graph(In in) 从标准输入流in中读入一幅图
int V() 顶点数
int E() 边数
void addEdge(int v, int w) 向图中添加一条边
Iterable<Integer> adj(int v) 和v相邻的所有顶点
String toString() 对象的字符串表示
最常用的图处理代码
//计算v的度数
public static int degree(Graph G, int v) {
int degree = 0;
for (int w : G.adj(v)) degree++;
return degree;
}
//计算所有顶点的最大度数
public static int maxDegree(Graph G) {
int max = 0;
for (int v = 0; v < G.V(); v++) {
if (degree(G, v) > max)
max = degree(G, v);
}
return max;
}
//计算所有定点的平均度数
public static double avgDegree(Graph G) {
return 2.0 * G.E() / G.V();
}
//计算自环的个数
public static int numberOfSelfLoops(Graph G) {
int count = 0;
for (int v = 0; v < G.V(); v++) {
for (int w : G.adj(v)) {
if (w == v) count++;
}
}
//每一条边都被标记过两次
return count / 2;
}
2.3 图的几种表示方法
图处理实现API必须满足以下两个要求:
- 它必须为可能在应用中碰到的各种类型的图预留出足够的空间
- Graph的实例方法的实现一定要快——它们是开发处理图的各种用例的基础
下面是图的三种表示方法:
- 邻接矩阵:我们可以使用一个V乘V的布尔矩阵来表示,但对于大图(上百万顶点)来说,
VxV个布尔值所需的空间是不能满足的。 - 边的数组:我们可以使用一个Edge类,它含有两个int实例变量。这种方法简单却不满足第二个条件——要实现
adj()需要检查图中的所有边 - 邻接表数组:以顶点为索引的列表数组,其中的每个元素都是和该顶点相邻的顶点列表。
2.4 邻接表的数据结构
非稠密图的标准表示称为邻接表的数据结构,它将每个顶点的所有相邻顶点都保存在该顶点对应的元素所指向的一张链表中。我们使用这个数组就是为了快速访问给定顶点的邻接顶点列表。
Graph数据类型
class Graph{
private final int V; //顶点数目
private int E; //边的数目
private Set<Integer>[] adj; //邻接表
public Graph(int V, int[][] edges) {
this.V = V;
adj = (HashSet<Integer>[]) new HashSet[V];
for (int v = 0; v < V; v++) {
adj[v] = new HashSet<Integer>();
}
for (int[] edge : edges) {
int w = edge[0]; //第一个顶点
int v = edge[1]; //第二个顶点
addEdge(w, v);
}
}
public void addEdge(int w, int v) {
adj[w].add(v);
adj[v].add(w);
E++;
}
public int V() {
return V;
}
public int E() {
return E;
}
public Set<Integer> adj(int v) {
return adj[v];
}
}
注:为了方便,相对于《算法》第四版中的代码有所修改

创建上图的邻接表数组测试代码如下
/*** main ***/
public class GraphTest {
public static void main(String[] args) {
int V = 6;
int[][] edges = {
{
0, 1}, {
0, 2}, {
0, 5}, {
1, 2}, {
2, 3}, {
2, 4}, {
3, 4}, {
3, 5}};
Graph g = new Graph(V, edges);
System.out.println("顶点数为:" + g.V());
System.out.println("边数为:" + g.E());
HashSet<Integer> set = (HashSet<Integer>) g.adj(2);
System.out.println("顶点2包含的边有:");
for (Integer v : set) {
System.out.println(v);
}
}
}
2.5 深度优先搜索(DFS)
深度优先搜索适合解决单点路径问题
class DepthFirstSearch{
private boolean[] marked;
private int count;
public DepthFirstSearch(Graph G, int s) {
marked = new boolean[G.V()];
dfs(G, s);
}
private void dfs(Graph G, int v) {
//System.out.println("结" + v + "已被标记");
marked[v] = true;
count++;
for (int w : G.adj(v)) {
if (!marked[w]) {
dfs(G, w);
}
}
}
public int getCount() {
return count;
}
}
从结点0开始遍历上图,遍历顺序为[0, 1, 2, 3, 4, 5]
使用深度优先搜索查找图中的路径
class DepthFirstPaths{
private boolean[] marked;
private int[] edgeTo; //从起点到一个顶点的已知路径上的最后一个顶点(父链接数组)
private final int s; //起点
public DepthFirstPaths(Graph G, int s) {
marked = new boolean[G.V()];
edgeTo = new int[G.V()];
this.s = s;
dfs(G, s);
}
private void dfs(Graph G, int v) {
marked[v] = true;
for (int w : G.adj(v)) {
if (!marked[w]) {
edgeTo[w] = v;
dfs(G, w);
}
}
}
public boolean hasPathTo(int v) {
return marked[v];
}
public Stack<Integer> pathTo(int v) {
if (!hasPathTo(v)) return null;
Stack<Integer> path = new Stack<Integer>();
for (int x = v; x != s; x = edgeTo[x]) {
path.push(x);
}
path.push(s);
return path;
}
}
2.6 广度优先搜索(BFS)
广度优先搜索适合解决单点最短路径问题
使用广度优先搜索查找图中的路径
class BreadthFirstPaths{
private boolean[] marked;
private int[] edgeTo; //父链接数组
private final int s; //起点
public BreadthFirstPaths(Graph G, int s) {
marked = new boolean[G.V()];
edgeTo = new int[G.V()];
this.s = s;
bfs(G, s);
}
private void bfs(Graph G, int s) {
Queue<Integer> queue = new ArrayDeque<>();
marked[s] = true; //标记起点
queue.offer(s);
while (!queue.isEmpty()) {
int v = queue.poll();
for (int w : G.adj(v)) {
if (!marked[w]) {
edgeTo[w] = v;
marked[w] = true;
queue.offer(w);
}
}
}
}
public boolean hasPathTo(int v) {
return marked[v];
}
public Stack<Integer> pathTo(int v) {
if (!hasPathTo(v)) return null;
Stack<Integer> path = new Stack<Integer>();
for (int x = v; x != s; x = edgeTo[x]) {
path.push(x);
}
path.push(s);
return path;
}
}
命题B:对于从s可达的任意顶点v,广度优先搜索都能找到一条从s到v的最短路径
命题B(续):广度优先搜索所需的时间在最坏情况下和
V+E成正比
相应测试代码如下
/*** main ***/
public class GraphTest {
public static void main(String[] args) {
int V = 6;
int[][] edges = {
{
0, 1}, {
0, 2}, {
0, 5}, {
1, 2}, {
2, 3}, {
2, 4}, {
3, 4}, {
3, 5}};
Graph g = new Graph(V, edges);
System.out.println("顶点数为:" + g.V());
System.out.println("边数为:" + g.E());
HashSet<Integer> set = (HashSet<Integer>) g.adj(2);
System.out.println("顶点2包含的边有:");
for (Integer v : set) {
System.out.println(v);
}
DepthFirstSearch df = new DepthFirstSearch(g, 0);
System.out.println("结点数为:" + df.getCount());
System.out.println("\n深度优先遍历:");
DepthFirstPaths dps = new DepthFirstPaths(g, 3);
Stack<Integer> stackd = dps.pathTo(1);
while (!stackd.isEmpty()) {
System.out.println("-> " + stackd.pop());
}
System.out.println("\n广度优先遍历:");
BreadthFirstPaths bps = new BreadthFirstPaths(g, 0);
Stack<Integer> stackb = bps.pathTo(5);
while (!stackb.isEmpty()) {
System.out.println("-> " + stackb.pop());
}
}
}
2.7 连通分量
连通是一种等价关系,它能够将所有顶点切分为等价类(连通分量);
连通分量的API
public class CC
------------------------------------------------------------------------------------
CC(Graph G) 预处理构造函数
boolean connected(int v, int w) v和w连通吗
int count() 连通分量数
int id(int v) v所在的连通分量标识符(0~count-1)
使用深度优先搜索找出图中的所有连通分量
class CC{
private boolean[] marked;
private int[] id;
private int count;
public CC(Graph G) {
marked = new boolean[G.V()];
id = new int[G.V()];
for (int s = 0; s < G.V(); s++) {
if (!marked[s]) {
dfs(G, s);
count++;
}
}
}
private void dfs(Graph G, int v) {
marked[v] = true;
id[v] = count;
for (int w : G.adj(v)) {
if (!marked[w]) {
dfs(G, w);
}
}
}
public boolean connected(int v, int w) {
return id[v] == id[w];
}
public int id(int v) {
return id[v];
}
public int count() {
return count;
}
}
union-find算法求连通分量
并查集相关知识见往期博客总结高级数据结构(Ⅰ)并查集(Union-Find)
class UF{
int N;
int count;
int[] id;
int[] sz;
UF(int N){
this.N = N;
count = N;
id = new int[N];
sz = new int[N];
for(int i = 0; i < N; i++) {
id[i] = i;
sz[i] = 1;
}
}
public int getCount() {
return count;
}
public void union(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if(pRoot != qRoot) {
if(sz[pRoot] < sz[qRoot]) {
id[pRoot] = id[qRoot];
sz[qRoot] += sz[pRoot];
}else {
id[qRoot] = id[pRoot];
sz[pRoot] += sz[qRoot];
}
count--;
}
}
public boolean connected(int p, int q) {
return find(p) == find(q);
}
private int find(int p) {
if(p == id[p]) return p;
id[p] = find(id[p]);
return id[p];
}
}
理论上,深度优先搜索比并并查集算法快,因为它能保证所需的时间是常数而并查集算法不行;但在实际应用中,这点差异微不足道。union-find 算法其实更快,因为它并不需要完整地构造并表示一幅图。更重要的是,union-find算法是一种动态算法(我们在任何时候都能用接近常数的时间检查两个顶点是否连通,甚至是在添加一条边的时候),但深度优先搜索则必须要对图进行预处理。因此,我们在完成只需要判断连通性或是需要完成有大量连通性查询和插入操作混合等类似的任务时,更倾向于使用union-find算法,而深度优先搜索则更适合实现图的抽象数据类型,因为它能有效地利用已有的数据结构。
从下面的测试就可以看出两者调用的差异
相应测试代码如下
/*** main ***/
public class GraphTest {
public static void main(String[] args) {
int V = 13;
int[][] edges = {
{
0, 1}, {
0, 2}, {
0, 5}, {
0, 6}, {
3, 4}, {
3, 5},
{
4, 5}, {
4, 6}, {
7, 8}, {
9, 10}, {
9, 11}, {
9, 12}, {
11, 12}};
Graph g = new Graph(V, edges);
System.out.println("\n深度优先遍历连通分量:");
CC cc = new CC(g);
System.out.println("共有"+ cc.count()+"个连通分量");
System.out.println("0 和 4 是否连通: " + cc.connected(0, 4));
System.out.println("4 和 7 是否连通: " + cc.connected(4, 7));
System.out.println("\n并查集求连通分量:");
UF uf = new UF(g.V());
//此处为了简单直接遍历边
for (int[] edge : edges) {
uf.union(edge[0], edge[1]);
}
System.out.println("共有"+ uf.getCount()+"个连通分量");
System.out.println("0 和 4 是否连通: " + uf.connected(0, 4));
System.out.println("4 和 7 是否连通: " + uf.connected(4, 7));
}
}
2.8 无环图的判断
给定的图是无环图吗?(假设不存在自环或平行边)
class Cycle{
private boolean[] marked;
private boolean hasCycle;
public Cycle(Graph G) {
marked = new boolean[G.V()];
for (int s = 0; s < G.V(); s++) {
if (!marked[s]) {
dfs(G, s, s);
}
}
}
private void dfs(Graph G, int v, int u) {
marked[v] = true;
for (int w : G.adj(v)) {
if (!marked[w]) {
dfs(G, w, v);
} else if (w != u) {
//若当前结点w已被标记且不等于其最初遍历父链接顶点u,表示有环
hasCycle = true;
}
}
}
public boolean hasCycle() {
return hasCycle;
}
}
2.9 二分图的判断
二分图也称为二部图。
双色问题:能够用两种颜色将图的所有顶点着色,使得任意一条边的两个端点的颜色都不相同。
无向图G为二分图的充要条件是:
- G中至少包含两个顶点
- G中所有的回路长度都必须是偶数
class TwoColor{
private boolean[] marked;
private boolean[] color;
private boolean isTwoColorable = true;
public TwoColor(Graph G) {
marked = new boolean[G.V()];
color = new boolean[G.V()];
for (int s = 0; s <G.V(); s++) {
if (!marked[s]) {
dfs(G, s);
}
}
}
private void dfs(Graph G, int v) {
marked[v] = true;
for (int w : G.adj(v)) {
if (!marked[w]) {
color[w] = !color[v];
dfs(G, w);
} else if (color[w] == color[v]) {
isTwoColorable = false;
return;
}
}
}
public boolean isBipartite() {
return isTwoColorable;
}
}
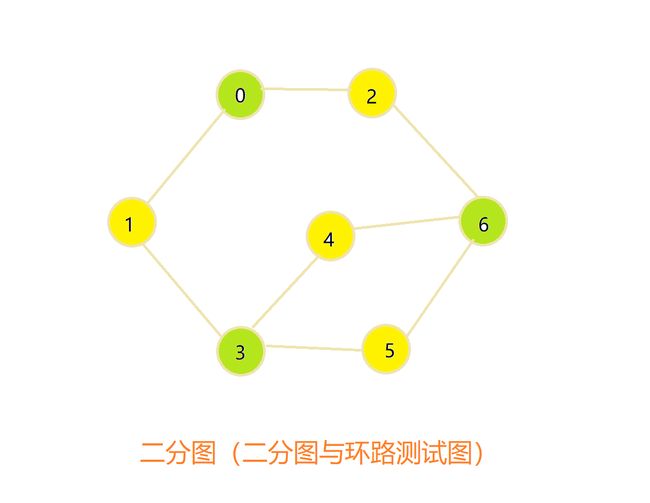
相应测试代码如下
/*** main ***/
public class GraphTest {
public static void main(String[] args)
int V = 7;
int[][] edges = {
{
0, 1}, {
0, 2}, {
1, 3}, {
2, 6}, {
3, 5}, {
3, 5}, {
4, 6}, {
5, 6}};
Graph g = new Graph(V, edges);
System.out.println("\n判断G中是否含有环:");
Cycle cy = new Cycle(g);
System.out.println(cy.hasCycle());
System.out.println("\n判断G是否是二部图:");
TwoColor tc = new TwoColor(g);
System.out.println(tc.isBipartite());
}
}
3 有向图
在有向图中,边是单向的:每条边所连接的两个顶点都是一个有序对,它们的邻接性是单向的。
实际生活中的典型有向图
| 应用 | 顶点 | 边 |
|---|---|---|
| 食物链 | 物种 | 捕食关系 |
| 互联网连接 | 网页 | 超链接 |
| 程序 | 模块 | 外部引用 |
| 手机 | 电话 | 呼叫 |
| 学术研究 | 论文 | 引用 |
| 金融 | 股票 | 交易 |
| 网络 | 计算机 | 网络连接 |
3.1 有向图术语
定义:一幅有方向性的图(或
有向图)是由一组顶点和一组有方向的边组成的,每条有方向的边都连接着有序的一对顶点。
我们称一条有向边由第一个顶点指出并指向第二个顶点。在一幅有向图中,一个顶点的出度为由该顶点指出的边的总数;一个顶点的入度为指向该顶点的边的总数。
定义:在一幅有向图中,
有向路径由一系列顶点组成,对于其中的每个顶点都存在一条有向边从它指向序列中的下一个顶点。有向环为一条至少含有一条边且起点和终点相同的有向路径。简单有向环是一条(除了起点和终点必须相同之外)不含有重复的顶点和边的环。路径或者环的长度即为其中所包含的边数。
3.2 有向图的数据类型
有向图的API
public class Digraph
-----------------------------------------------------------------------------------
Digraph(int V) 创建一幅含有V个顶点但没有边的有向图
Digraph(In in) 从输入流in中读入一幅有向图
int V() 顶点总数
int E() 边的总数
void addEdge(int v, int w) 添加一条边v->w
Iterable<Integer> adj<int v> 由v指出的边所连接的所有顶点
Digraph reverse() 该图的反向图
String toString() 对象的字符串表示
Digraph数据类型
class Digraph{
private final int V;
private int E;
private List<Integer>[] adj;
public Digraph(int V) {
this.V = V;
this.E = 0;
adj = new ArrayList[V];
for (int v = 0; v < V; v++) {
adj[v] = new ArrayList<Integer>();
}
}
public Digraph(int V, int[][] edges) {
this.V = V;
this.E = 0;
adj = new ArrayList[V];
for (int v = 0; v < V; v++) {
adj[v] = new ArrayList<Integer>();
}
for (int[] edge : edges) {
addEdge(edge[0], edge[1]);
}
}
public void addEdge(int w, int v) {
adj[w].add(v);
E++;
}
public int V() {
return V;
}
public int E() {
return E;
}
public List<Integer> adj(int v) {
return adj[v];
}
public Digraph reverse() {
Digraph R = new Digraph(V);
for (int v = 0; v < V; v++) {
for (int w : adj(v)) {
R.addEdge(w, v);
}
}
return R;
}
public String toString() {
String str = "";
for (int v = 0; v < V; v++) {
str += v + " : ";
for (int w : adj(v)) {
str += " -> " + w;
}
str += "\n";
}
return str;
}
}
注:有向图的深度优先遍历、广度优先遍历与无向图相同,在此不做介绍。
3.3 标记-清除的垃圾收集
多点可达性的一个重要的实际应用是在典型的内存管理系统中,包括许多Java的实现。在一幅有向图中,一个顶点表示一个对象,一条边则表示一个对象对另一个对象的引用。这个模型很好地表现了运行中的Java程序的内存使用状况。在程序执行的任何时候都有某些对象是可以被直接访问的,而不能通过这些对象访问到的所有对象都应该被回收以便释放内存。标记-清除的垃圾回收策略会为每个对象保留一个位做垃圾收集之用。它会周期性地运行一个类似于DirectedDFS的有向图可达性算法来标记所有可以被访问到的对象,然后清理所有对象,回收没有被标记的对象,以腾出内存供新的对象使用。
3.4 寻找有向环
class DirectedCycle{
private boolean[] marked;
private int[] edgeTo;
private Stack<Integer> cycle; //有向环中的所有顶点
private boolean[] onStack; //递归调用的栈上所有顶点
public DirectedCycle (Digraph G) {
onStack = new boolean[G.V()];
edgeTo = new int[G.V()];
marked = new boolean[G.V()];
for (int v = 0; v < G.V(); v++) {
if (!marked[v]) {
dfs(G, v);
}
}
}
private void dfs(Digraph G, int v) {
onStack[v] = true;
marked[v] = true;
for (int w : G.adj(v)) {
if (this.hasCycle()) return;
else if (!marked[w]) {
edgeTo[v] = w;
dfs(G, w);
} else if (onStack[w]){
cycle = new Stack<Integer>();
for (int x = v; x != w; x = edgeTo[x]) {
cycle.push(x);
}
cycle.push(w);
cycle.push(v);
}
}
onStack[v] = false;
}
public boolean hasCycle() {
return cycle != null;
}
public Stack<Integer> cycle() {
return cycle;
}
}
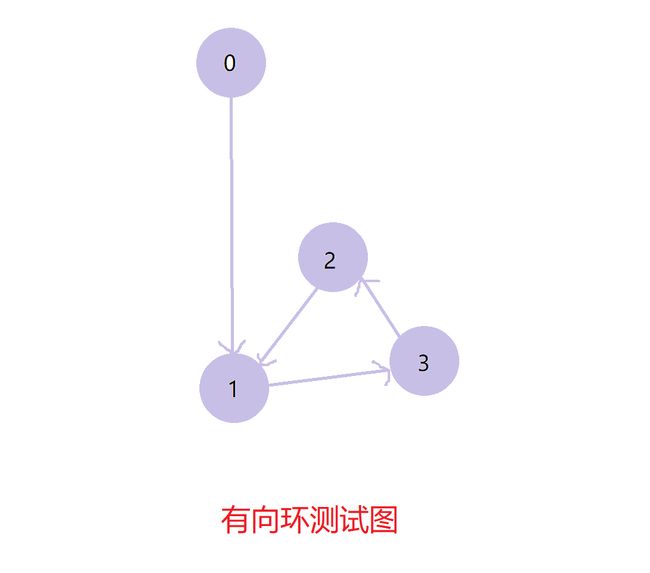
public class DigraphTest {
public static void main(String[] args) {
int V = 4;
int[][] edges = {
{
0, 1}, {
1, 3}, {
3, 2}, {
2, 1}};
Digraph g = new Digraph(V, edges);
DirectedCycle dc = new DirectedCycle(g);
if (dc.hasCycle()) {
Stack<Integer> cycle = dc.cycle();
String cycleV = "";
while (!cycle.isEmpty()) {
cycleV += "->" + String.valueOf(cycle.pop());
}
System.out.println("环为 : " + cycleV);
}
}
}
3.5 有向图基于DFS搜索的顶点排序
- 前序:在递归调用之前将顶点加入
队列 - 后序:在递归调用之后将顶点加入
队列 - 逆后序:在递归调用之后将顶点压入
栈

注:下面的测试均以此图为主
class DepthFirstOrder{
private boolean[] marked;
private Queue<Integer> pre; //所有顶点的前序排列
private Queue<Integer> post; //所有顶点的后序排列
private Stack<Integer> reversepost; //所有顶点的逆后续排列
public DepthFirstOrder(Digraph G) {
pre = new ArrayDeque<>();
post = new ArrayDeque<>();
reversepost = new Stack<>();
marked = new boolean[G.V()];
for (int v = 0; v < G.V(); v++) {
if (!marked[v]) {
dfs(G, v);
}
}
}
private void dfs(Digraph G, int v) {
pre.offer(v);
marked[v] = true;
for (int w : G.adj(v)) {
if (!marked[w]) {
dfs(G, w);
}
}
post.offer(v);
reversepost.push(v);
}
public Iterable<Integer> pre() {
return pre;
}
public Iterable<Integer> post() {
return post;
}
//注意:此处不用迭代器的原因是迭代器对栈的遍历是从栈底开始的
public Stack<Integer> reversePost() {
return reversepost;
}
}
上图的三种排列顺序为
前序排列为:0, 1, 5, 4, 6, 9, 10, 11, 12, 2, 3, 7, 8
后序排列为:1, 4, 5, 10, 12, 11, 9, 6, 0, 3, 2, 7, 8
逆后序排列为:8, 7, 2, 3, 0, 6, 9, 11, 12, 10, 5, 4, 1
测试代码如下
public class DigraphTest {
public static void main(String[] args) {
int V = 13;
int[][] edges = {
{
0, 1}, {
0, 5}, {
0, 6}, {
2, 0}, {
2, 3}, {
3, 5}, {
5, 4},
{
6, 4}, {
6, 9}, {
7, 6}, {
8, 7}, {
9, 10}, {
9, 11}, {
9, 12}, {
11, 12}};
Digraph g = new Digraph(V, edges);
DepthFirstOrder df = new DepthFirstOrder(g);
Iterable<Integer> pre = df.pre();
String spre = "";
Iterator ipre = pre.iterator();
while (ipre.hasNext()) {
spre += ipre.next() + ", ";
}
System.out.println("前序排列为:" + spre);
//同理可得后序排列,逆后续排列
Iterable<Integer> post = df.post();
String spost = "";
Iterator ipost = post.iterator();
while (ipost.hasNext()) {
spost += ipost.next() + ", ";
}
System.out.println("后序排列为:" + spost);
Stack<Integer> reversePost = df.reversePost();
String sreversePost = "";
while (!reversePost.isEmpty()) {
sreversePost += reversePost.pop() + ", ";
}
System.out.println("逆后序排列为:" + sreversePost);
}
}
3.6 拓扑排序
命题: 当且仅当一幅有向无环图是无环图时它才能进行拓扑排序
命题: 一幅有向图的拓扑排序顺序即为所有顶点的逆后续排列
class Topological{
private Stack<Integer> order; //顶点的拓扑排序
public Topological(Digraph G) {
DirectedCycle cycleFinder = new DirectedCycle(G);
if (!cycleFinder.hasCycle()) {
DepthFirstOrder dfs = new DepthFirstOrder(G);
order = dfs.reversePost();
}
}
public Stack<Integer> order() {
return order;
}
//是有向无环图吗
public boolean isDAG() {
return order != null;
}
}
基于队列的拓扑排序
class BaseQueueTopological{
private Queue<Integer> order;
private int[] degrees;
BaseQueueTopological(Digraph G) {
order = new ArrayDeque<>();
DirectedCycle cycleFinder = new DirectedCycle(G);
if (!cycleFinder.hasCycle()) {
degrees = new int[G.V()];
for (int v = 0; v < G.V(); v++) {
for (int w : G.adj(v)) {
degrees[w]++;
}
}
ordered(G);
}
}
private void ordered(Digraph G) {
Queue<Integer> queue = new ArrayDeque<>();
for (int v = 0; v < G.V(); v++) {
if (degrees[v] == 0) {
queue.offer(v);
}
}
while (!queue.isEmpty()) {
int v = queue.poll();
order.offer(v);
for (int w : G.adj(v)) {
degrees[w]--;
if (degrees[w] == 0) {
queue.offer(w);
}
}
}
}
public Iterable<Integer> order() {
return order;
}
//是有向无环图吗
public boolean isDAG() {
return !order.isEmpty();
}
}
测试代码如下
输出为:
拓扑排序为: 2, 8, 0, 3, 7, 1, 5, 6, 4, 9, 10, 11, 12,
public class DigraphTest {
public static void main(String[] args) {
int V = 13;
int[][] edges = {
{
0, 1}, {
0, 5}, {
0, 6}, {
2, 0}, {
2, 3}, {
3, 5}, {
5, 4},
{
6, 4}, {
6, 9}, {
7, 6}, {
8, 7}, {
9, 10}, {
9, 11}, {
9, 12}, {
11, 12}};
Digraph g = new Digraph(V, edges);
BaseQueueTopological bt = new BaseQueueTopological(g);
if (!bt.isDAG()) {
System.out.println("有环");
} else {
Iterator<Integer> order = bt.order().iterator();
String so = "";
while (order.hasNext()) {
so += order.next() + ", ";
}
System.out.println("拓扑排序为: " + so);
}
}
}
3.7 有向图的强连通性
定义:如果两个顶点v和w是相互可达的,则称它们为
强连通的。也就是说,也就是说,既存在一条从v到w的有向路径,也存在一条从w到v的有向路径。如果一幅有向图中的任意两个顶点都是强连通的,则称这幅有向图也是强连通的。
两个顶点是强连通的当且仅当它们都在一个普通的有向环中。
强连通分量
和无向图中的连通性一样,有向图中的强连通性也是一种顶点之间的等价关系,因为它有着以下性质。
- 自反性
- 对称性
- 传递性
作为一种等价关系,强连通性将所有顶点分为了一些等价类,每个等价类都是由相互均为强连通的顶点的最大子集组成的,我们将这些子集称为强连通分量。
- 一个含有V个顶点的有向图含有1~V个强连通分量
- 一个强连通图只含有一个强连通分量
- 一个有向无环图中含有V个强连通分量
需要注意的是强连通分量的定义是基于顶点的,而非边。
3.8 Kosaraju算法求强连通分量
Kosaraju(科萨拉朱)算法的步骤:
- 在给定的一幅有向图G中,使用DepthFirstOrder来计算它的
反图(即转置图)G的逆后续排列 - 在G中按照得到的逆后续排列进行标准的
深度优先搜索来访问未标记结点,其每一次调用递归所标记的顶点都在同一个强连通分量中
(封住连通分量往外走的路)
算法原理:
- 反图与原图的强连通分量相同
- 若原图能从分量1走到分量2,则反图不能从分量1走到分量2
class KosarajuSCC{
private boolean[] marked;
private int[] id; //强连通分量的标识符
private int count; //强连通分量的数量
public KosarajuSCC(Digraph G) {
marked = new boolean[G.V()];
id = new int[G.V()];
DepthFirstOrder order = new DepthFirstOrder(G.reverse());
Stack<Integer> reversePost = order.reversePost();
while (!reversePost.isEmpty()) {
int w = reversePost.pop();
if (!marked[w]) {
dfs(G, w);
count++;
}
}
}
private void dfs(Digraph G, int v) {
marked[v] = true;
id[v] = count;
for (int w : G.adj(v))
if (!marked[w])
dfs(G, w);
}
public boolean stronglyConnected(int v, int w) {
return id[v] == id[w];
}
public int id(int v) {
return id[v];
}
public int count() {
return count;
}
}
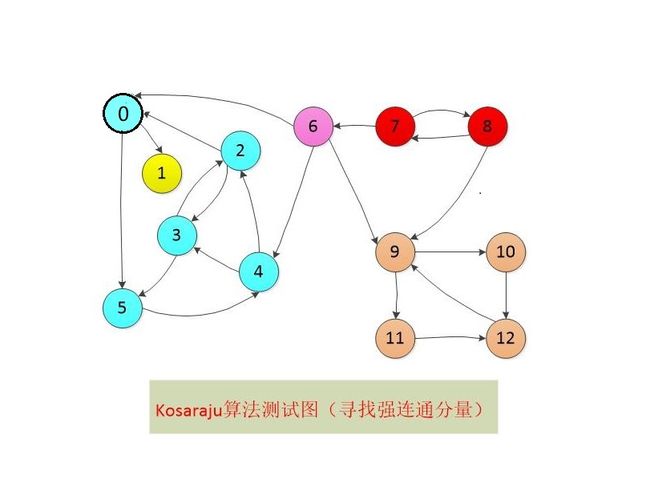
测试代码如下
public class DigraphTest {
public static void main(String[] args) {
int V = 13;
int[][] edges = {
{
0, 1}, {
0, 5}, {
2, 0}, {
2, 3}, {
3, 2}, {
3, 5}, {
4, 2},
{
4, 3}, {
5, 4}, {
6, 0}, {
6, 4}, {
6, 9}, {
7, 6}, {
7, 8}, {
8, 7},
{
8, 9}, {
9, 10}, {
9, 11}, {
10, 12}, {
11, 12}, {
12, 9}};
Digraph g = new Digraph(V, edges);
KosarajuSCC ko = new KosarajuSCC(g);
System.out.println("共有几个连通分量:" + ko.count());
for (int i = 0; i < ko.count(); i++) {
System.out.print("第" + (i + 1) + "个连通分量:");
for (int v = 0; v < g.V(); v++) {
if (ko.id(v) == i) {
System.out.print(v + ", ");
}
}
System.out.println("");
}
}
}
测试上图输出结果如下
共有几个连通分量:5
第1个连通分量:9, 10, 11, 12,
第2个连通分量:1,
第3个连通分量:0, 2, 3, 4, 5,
第4个连通分量:6,
第5个连通分量:7, 8,
参考资料:《算法》第四版
B站up主<董晓算法>:强连通分量Kosaraju算法——信息学奥赛培训课程

