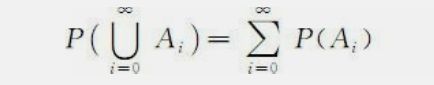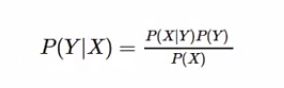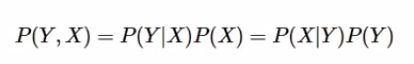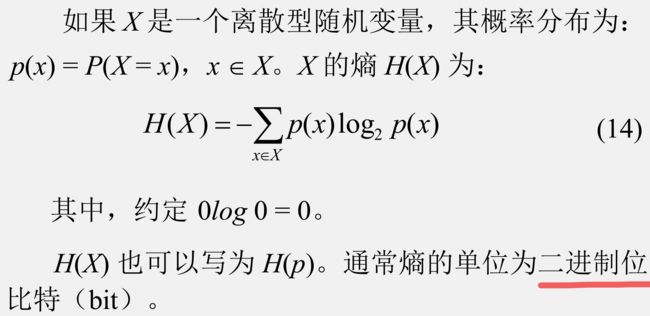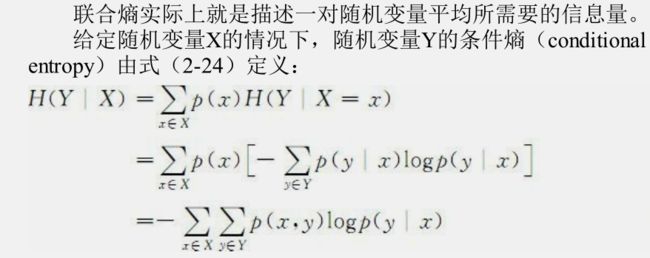在基于统计方法的自然语言处理研究中,有关统计学和信息论等方面的知识是不可缺少的基础,所以这一篇主要回顾一些基本的数学知识,侧重点在怎样在自然语言处理中使用这些数学知识。所以写的会侧重概念的介绍,觉得没有掌握的同学都可以查资料深入看一下
概率论基本概念
1.概率
概率(probability)是从随机试验中的事件到实数域的映射函数,用以表示事件发生的可能性
数学定义:概率是从随机实验中的事件到实数域的函数,用以表示事件发生的可能性
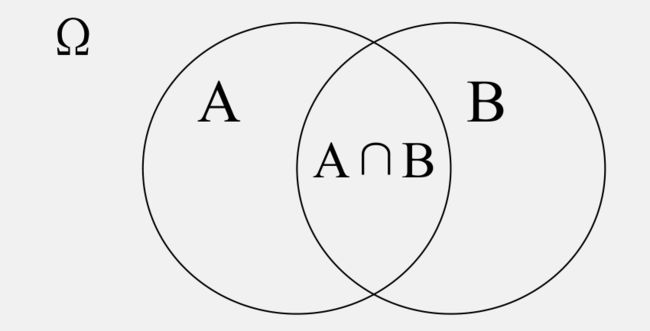
如果用P(A)作为事件A的概率,Ω是试验的样本空间,则概率函数必须满足如下三条公理:
公理1(非负性) P(A)≥0(概率不可能为负的)
公理2(规范性) P(Ω)=1(所有概率加起来必须要等于1,也就是归一性)
公理3(可列可加性) 对于可列无穷多个事件A 1 ,A 2 ,…,如果事件两两互不相容,即对于任意的i和j(i≠j),事件A i 和A j 不相交(A i ∩A j =∅),则有:
1.1.怎么计算概率?
概率是一个很抽象的概念,要想算一个时间发生的可能性,只能从有限的空间中去得到,这个有限的空间我们就使用最大似然估计得方法来算某个样本空间中的某个时间出现(经过若干次实验)的次数(或叫相对频率)
2.最大似然估计
如果进行n次实验(n趋向于无穷大),我们把某个时间发生的相对频率叫默认为时间的发生概率,用这样的方法来计算概率,这个方法就叫做最大似然估计(谁起的名字)
3.条件概率
条件概率 P(A|B) 给出了在已知事件 B 发生的情况下,事件 A 发生的概率。一般地,P(A|B) ≠ P(A)
4.贝叶斯法则(重点)
4.1贝叶斯方法历史悠久...有着坚实的理论基础,处理很多的问题直接又高效,很多高级的自然语言处理模型都是从它演化而来,很多fancy的模型看起来nb,但往往用的时候才发现还是贝叶斯效果好...
4.2贝叶斯公式
这个公式我觉得大家都学过吧,没想到在自然语言处理中有遇上了,这公式我记得高中时通常是和袋子里的球一起出现的....
它其实是由以下的联合概率公式推导来的:
其中P(Y)叫做先验概率,P(Y|X)叫做后验概率,P|(Y,X)叫做联合概率,就这些,这么nb的东西就这两公式
这公式用的地方那可是非常多,我举几个例子:垃圾邮件识别、中文分词、词性标注、文本分类等等
贴个列子:语音识别问题
5.期望值
期望值(expectation)是指随机变量所取值的概率平均
6.方差
一个随机变量的方差(variance)描述的是该随机变量的值偏离其期望值的程度
信息论基本概念
1.熵
香农(Claude Elwood Shannon)于1940年获得麻省理工学院数学博士学位和电子工程硕士学位后,于1941年加入了贝尔实验室数学部,并在那里工作了15年。1948年6月和10月,由贝尔实验室出版的《贝尔系统技术》杂志连载了香农博士的文章《通讯的数学原理》,该文奠定了香农信息论的基础
1.1定义
它实际上反映的是对某一个随机变量要进行编码的时候所采用的比特位的个数(直白的解释),所以熵又称为自信息(self-information),表示信源X 每发一个符号(不论发什么符号)所提供的平均信息量。熵也可以被视为描述一个随机变量的不确定性的数量。一个随机变量的熵越大,它的不确定性越大。那么,正确估计其值的可能性就越小。越不确定的随机变量越需要大的信息量用以确定其值
也就是说你要预测某一个信息量,对某一个信息量进行编码的时候,它熵越大,你需要的比特位越多,因为越小的话你描述的随机变量的值是月确定的,如果你只要两种情况的话,你只需要一个比特位就可以描述了,要么是1,要么是1.
2.联合熵
联合熵实际上就是描述一对随机变量平均所需要的信息量
和联合概率
3.条件熵
同样是合条件概率很想吧
4.相对熵
相对熵又称Kullback-Leibler差异,或简称KL距离,是衡量相同事件空间里两个概率分布相对差距的测度,当两个随机分布完全相同时,相对熵为0。当两个随机分布的差别增加时,其相对熵期望值也增大
5.交叉熵(cross entropy)
这个概念在神经网络中也经常提到,听过吴恩达老师的机器学习课程的应该都知道,交叉熵越小越能证明模型有效
6.困惑度
困惑度是替代交叉熵用来衡量模型好坏的,实际上就是取一个2的指数次方,公式就可以看出来,那么为啥不用交叉熵,实际上交叉熵算出来总是小数,因为取得log嘛,小数就不利于我们的计算,于是就再取个2次方,主要就是为了计算起来方便
于是语言模型设计的任务就是寻找困惑度最小的模型,使其最接近真实的语言
实际上交叉熵和困惑度就是一个概念啊,都是越小越好,大家不要被迷惑了
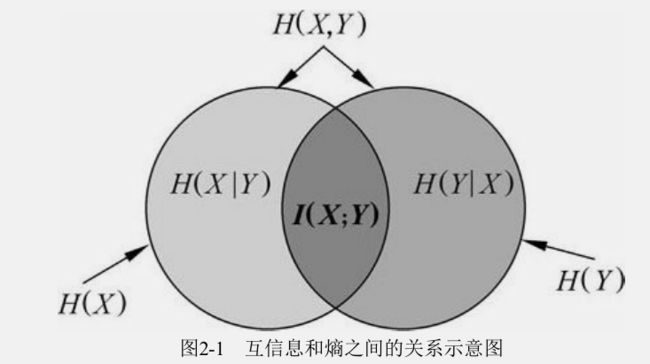
7.互信息
这个互信息反映的是在知道了Y的值以后X的不确定性的减少量。可以理解为Y的值透露了多少关于X的信息量
用到的概念大概就这么多,如果遇到其他的再找资料看看就好
END