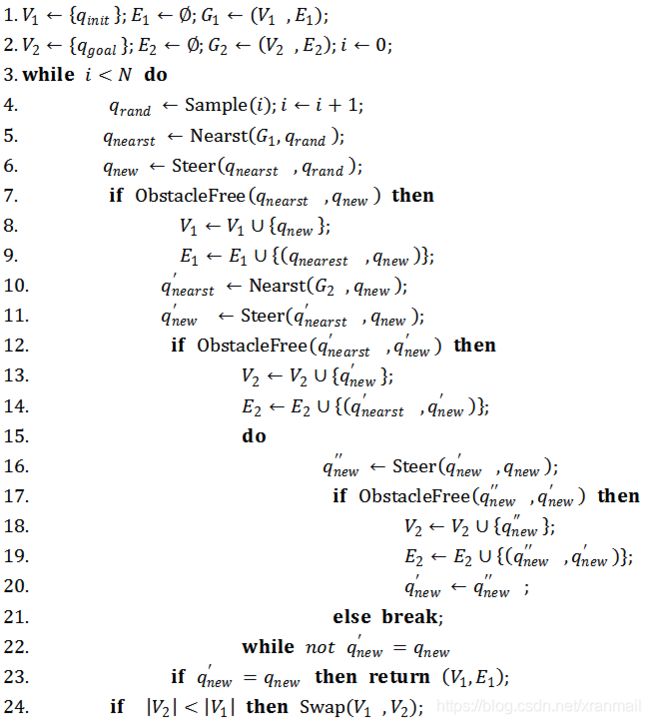基本的路径规划算法
随机路图法(Probabilistic Road Map,PRM):传统的人工势场、单元分解法需要对空间中的障碍物进行精确建模,当环境中的障碍物较为复杂时,将导致规划算法计算量较大。基于随机采样技术的PRM法可以有效解决高维空间和复杂约束中的路径规划问题。PRM是一种基于图搜索的方法,它将连续空间转换成离散空间,再利用A*等搜索算法在路线图上寻找路径,以提高搜索效率。这种方法能用相对少的随机采样点来找到一个解,对多数问题而言,相对少的样本足以覆盖大部分可行的空间,并且找到路径的概率为1(随着采样数增加,P(找到一条路径)指数的趋向于1)。显然,当采样点太少,或者分布不合理时,PRM算法是不完备的,但是随着采用点的增加,也可以达到完备。所以PRM是概率完备且不最优的。
快速扩展随机树法(RRT): 是基于树状结构的搜索算法,RRT算法是从起始点开始向外拓展一个树状结构,而树状结构的拓展方向是通过在规划空间内随机采点确定的。与PRM类似,该方法是概率完备且不最优的。
function BuildRRT(qinit, K, Δq)
T.init(qinit)
for k = 1 to K
qrand = Sample() -- chooses a random configuration
qnearest = Nearest(T, qrand) -- selects the node in the RRT tree that is closest to qrand
if Distance(qnearest, qgoal) < Threshold then
return true
qnew = Extend(qnearest, qrand, Δq) -- moving from qnearest an incremental distance in the direction of qrand
if qnew ≠ NULL then
T.AddNode(qnew)
return false
function Sample() -- Alternatively,one could replace Sample with SampleFree(by using a collision detection algorithm to reject samples in C_obstacle
p = Random(0, 1.0)
if 0 < p < Prob then
return qgoal
elseif Prob < p < 1.0 then
return RandomNode()初始化时随机树T只包含一个节点:根节点qinit。首先Sample函数从状态空间中随机选择一个采样点qrand(4行);然后Nearest函数从随机树中选择一个距离qrand最近的节点qnearest(5行);最后Extend函数通过从qnearest向qrand扩展一段距离,得到一个新的节点qnew(8行)。如果qnew与障碍物发生碰撞,则Extend函数返回空,放弃这次生长,否则将qnew加入到随机树中。重复上述步骤直到qnearest和目标点qgoal距离小于一个阈值,则代表随机树到达了目标点,算法返回成功(6~7行)。为了使算法可控,可以设定运行时间上限或搜索次数上限(3行)。如果在限制次数内无法到达目标点,则算法返回失败。
为了加快随机树到达目标点的速度,简单的改进方法是:在随机树每次的生长过程中,根据随机概率来决定qrand是目标点还是随机点。在Sample函数中设定参数Prob,每次得到一个0到1.0的随机值p,当0
Bidirectional RRT / RRT Connect:基本的RRT每次搜索都只有从初始状态点生长的快速扩展随机树来搜索整个状态空间,如果从初始状态点和目标状态点同时生长两棵快速扩展随机树来搜索状态空间,效率会更高。为此,基于双向扩展平衡的连结型双树RRT算法,即RRT_Connect算法被提出.
该算法与原始RRT相比,在目标点区域建立第二棵树进行扩展。每一次迭代中,开始步骤与原始的RRT算法一样,都是采样随机点然后进行扩展。然后扩展完第一棵树的新节点qnew,以这个新的目标点作为第二棵树扩展的方向。同时第二棵树扩展的方式略有不同(15~22行),首先它会扩展第一步得到q'new如果没有碰撞,继续往相同的方向扩展.第二步,直到扩展失败或者q'new=qnew表示与第一棵树相连了,即connect了,整个算法结束。当然每次迭代中必须考虑两棵树的平衡性,即两棵树的节点数的多少(也可以考虑两棵树总共花费的路径长度),交换次序选择“小”的那棵树进行扩展。这种双向的RRT技术具有良好的搜索特性,比原始RRT算法的搜索速度、搜索效率有了显著提高,被广泛应用。首先,Connect算法较之前的算法在扩展的步长上更长,使得树的生长更快;其次,两棵树不断朝向对方交替扩展,而不是采用随机扩展的方式,特别当起始位姿和目标位姿处于约束区域时,两棵树可以通过朝向对方快速扩展而逃离各自的约束区域。这种带有启发性的扩展使得树的扩展更加贪婪和明确,使得双树RRT算法较之单树RRT算法更加有效。
Dijkstra算法:狄克斯特拉算法。是从一个特定的顶点(又可称为原点,可自己定义)到其余各顶点的最短路径算法,解决的是有向图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
步骤:a.初始时,S只包含源点,即S={v},v的距离为0。U包含除v外的其他顶点,即:U={其余顶点},若v与U中顶点u有边,则{u,v}正常有权值,若u不是v的出边邻接点,则{u,v}权值为∞。
b.从U中选取一个距离v最小的顶点k,把k,加入S中(该选定的距离就是v到k的最短路径长度)。
c.以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u的距离(经过顶点k)比原来距离
(不经过顶点k)短,则修改顶点u的距离值,修改后的距离值的顶点k的距离加上边上的权。
d.重复步骤b和c直到所有顶点都包含在S中。
广度优先搜索(BFS)算法按照类似的流程运行,不同的是它能够评估(称为启发式的)任意结点到目标点的代价。与选择离初始结点最近的结点不同的是,它选择离目标最近的结点。BFS不能保证找到一条最短路径。然而,它比Dijkstra算法快的多,因为它用了一个启发式函数(heuristic )快速地导向目标结点。例如,如果目标位于出发点的南方,BFS将趋向于导向南方的路径。在下面的图中,越黄的结点代表越高的启发式值(移动到目标的代价高),而越黑的结点代表越低的启发式值(移动到目标的代价低)。这表明了与Dijkstra 算法相比,BFS运行得更快。
A*算法:A*是路径搜索中最受欢迎的选择,因为它相当灵活,并且能用于多种多样的情形之中。和其它的图搜索算法一样,A*潜在地搜索图中一个很大的区域。和Dijkstra一样,A*能用于搜索最短路径。和BFS一样,A*能用启发式函数(注:原文为heuristic)引导它自己。在简单的情况中,它和BFS一样快。公式表示为: f(n)=g(n)+h(n),其中, f(n) 是从初始状态经由状态n到目标状态的代价估计,g(n) 是在状态空间中从初始状态到状态n的实际代价,h(n) 是从状态n到目标状态的最佳路径的估计代价。
开始搜索: 搜索的从A点开始,首先将A点加入开启列表,此时取开启列表中的最小值,初始阶段开启列表中只有A一个节点,因此将A点从开启列表中取出,将A点加入关闭列表。 取出A点的相邻点,将相邻点加入开启列表。如图2所示,此时A点即为相邻点的父节点。图中箭头指向父节点。将相邻点与A点加入追溯表中。
计算耗费评分:对相邻点,一次计算每一点的g,h,最后得到f
选最小值,再次搜索:选出开启列表中的F值最小的节点,将此节点设为当前节点,移出开启列表,同时加入关闭列表。 取出当前点的相邻点,当相邻点为关闭点或者墙时,不操作。此外,查看相邻点是否在开启列表中,如不在开启列表中将相邻点加入开启列表。如相邻点已经在开启列表中,则需要进行G值判定。
G值判定: 对于相邻点在开启列表中的,计算相邻点的G值,计算按照当前路径的G值与原开启列表中的G值大小。如果当前路径G值小于原开启列表G值,则相邻点以当前点为父节点,将相邻点与当前点加入追溯表中。同时更新此相邻点的H值。如果当前路径G值大于等于原开启列表G值,则相邻点按照原开启列表中的节点关系,H值不变。因为图示中,当前点G值比原开启列表G值大,因此节点关系按照原父子关系和F值。
计算耗费评分,选最小值:此时计算开启列表中F值最小的点,将此节点设为当前节点,并列最小F值的按添加开启列表顺序,以最新添加为佳。
重复搜索判定工作: 直到当goal点B加入开启列表中,则搜索完成。此时事实上生成的路径并一定是最佳路径,而是最快计算出的路径。若判定标准改为当goal点B加入关闭列表中搜索完成,则得出路径是最佳路径,但此时计算量较前者大。 当没有找到goal点,同时开启列表已空,则搜索不到路径。结束搜索。
生成路径:由goal点B向上逐级追溯父节点,追溯至起点A,此时各节点组成的路径即使A*算法生成的最优路径。
while(OPEN!=NULL)
{ 从OPEN表中取f(n)最小的节点n;
if(n节点==目标节点) break;
for(当前节点n的每个子节点X)
{ 计算f(X);
if(X in OPEN)
if(新的f(X)保存路径,即从终点开始,每个节点沿着父节点移动直至起点,这就是你的路径。
迪杰斯特拉算法,类似于广度优先遍历,利用源点到当前节点的代价值作为指标,其一定可以获得从原点到目标节点的最短路,但是其访问的节点数很多。当地图中包含障碍物时,迪杰斯特拉算法,仍然可以获得最短路径的路径,最好优先搜索的节点尽管少,但是其不能获得最优解. A*算法,参考了从原点到当前节点的代价值和当前节点到目标节点启发值,综合了迪杰斯特拉算法和做好优先搜索算法优点,在有障碍物和无障碍物的地图上,可以像迪杰斯特拉算法一样求得最短路径同时,同时能够像最好优先搜索一样减少搜索范围,减少搜索节点的数目。
人工势场法:它的基本思想是将机器人在周围环境中的运动,设计成一种抽象的人造引力场中的运动,目标点对移动机器人产生“引力”,障碍物对移动机器人产生“斥力”,最后通过求合力来控制移动机器人的运动。应用势场法规划出来的路径一般是比较平滑并且安全,但是这种方法存在局部最优点问题。
还有遗传算法:粒子群优化算法:改进蚁群算法:等待补充。