二叉树(二)
二叉树(二)
1:二叉树链式结构的遍历
所谓遍历(Traversal)是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。访问结点所做 的操作依赖于具体的应用问 题。 遍历是二叉树上最重要的运算之一,是二叉树上进行其它运算之基础。
1.1:前序/中序/后序的递归结构遍历:是根据访问结点操作发生位置命名
1. NLR:前序遍历(先根 后左子树 其次右子树)——访问根结点的操作发生在遍历其左右子树之前。
2. LNR:中序遍历(先左子树 后根节点 其次右子树)——访问根结点的操作发生在遍历其左右子树之中(间)。
3. LRN:后序遍历(先左子树 后右子树 其次根节点)——访问根结点的操作发生在遍历其左右子树之后。
4. 层序遍历:设二叉树的根节点所在 层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层 上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
备注:前三者叫深度优先遍历 最后一个叫广度优先遍历
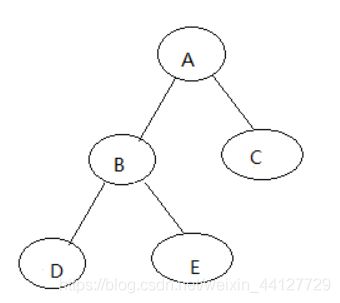
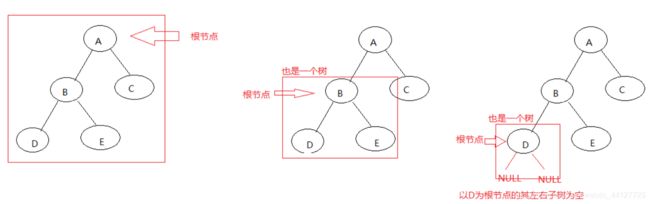
图解:
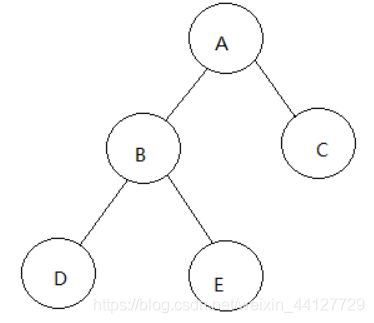
如上图是一个完全二叉树
1:先序遍历
A B D (NULL) (NULL) E (NULL) (NULL) C (NULL) (NULL)
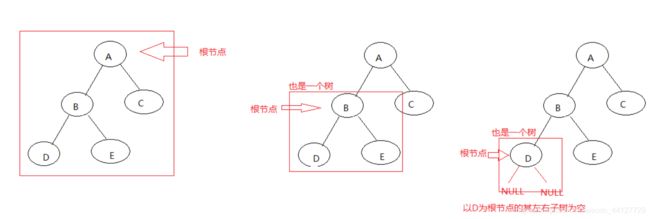
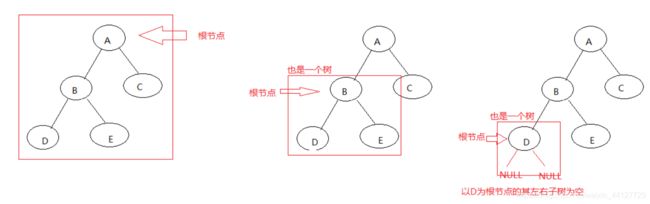
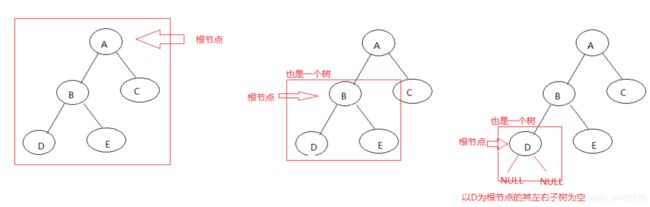
步骤1:把ABCDE看成一棵树 先访问根节点A 然后要访问其左子树
步骤2:但是对于以B为根节点的BDC而言 他也是一棵树 所以先访问根节点B 然后要访问其左子树
步骤3:但是对于以D为根节点的D而言 他也是一棵树 只不过其左子树和右子树为NULL而已 所以先访问根节点D 然后访问左子树NULL 再访问右子树NULL
步骤4:以D为根节点的树访问完成 对于B而言就是其左子树访问完成 所以要访问右子树
步骤5:同理 对于E而言 以E为根节点的子树也是一棵树 只不过其左子树和右子树为NULL而已 所以先访问根节点R 然后访问左子树NULL 再访问右子树NULL
步骤6:以E为根节点的树访问完成 对于B而言就是其右子树访问完成 对于A而言 就是其左子树访问完成 所以要访问右子树C
步骤7:对于以C为根节点的子树而言 也是一棵树 只不过其左子树和右子树为NULL而已 所以先访问根节点C 然后访问左子树NULL 再访问右子树NULL
总结:一直到为空 这样之后 该二叉树就先序遍历完成了 只不过NULL再显示的时候不打印 所以只显示ABDEC
2:中序遍历
(NULL) D (NULL) B (NULL) E (NULL) A (NULL) C (NULL)
步骤1:把ABCDE看成是一棵树 先访问其左子树B
步骤2:但是对于以B为根节点的BDE而言 他也是一棵树 所以要先访问其左子树 D
步骤3:但是对于以D为根节点的D而言 他也是一棵树 只不过其左子树和右子树为NULL而已 所以先访问左子树NULL 再访问根节点D 然后访问右子树NULL
步骤4:以D为根节点的树访问完成 对于B这棵树而言 就是其左子树访问完成 要访问根节点B 然后再访问其右子树E
步骤5:同理 对于E而言 以E为根节点的子树也是一棵树 只不过其左子树和右子树为NULL而已 所以先访问左子树NULL 再访问根节点E 然后访问右子树NULL
步骤6:以E为根节点的树访问完成 对于以B为根节点的树而言 其就访问完成了 对于以A为根节点的树而言 相当于其左子树访问完成 接下来就是访问其根节点A 然后再访问其右子树C
步骤7:对于以C为根节点的子树而言 也是一棵树 只不过其左子树和右子树为NULL而已 所以先访问左子树NULL 再访问根节点C 然后访问右子树NULL
总结:一直到为空 这样之后 该二叉树就中序遍历完成了 只不过NULL再显示的时候不打印 所以只显示DBEAC
3:后序遍历
(NULL) (NULL) D (NULL) (NULL) E B (NULL) (NULL) C A
步骤1:把ABCDE看成是一棵树 先访问其左子树B
步骤2:但是对于以B为根节点的BDE而言 他也是一棵树 所以要先访问其左子树 D
步骤3:但是对于以D为根节点的D而言 他也是一棵树 只不过其左子树和右子树为NULL而已 所以先访问左子树NULL 再访问右子树NULL 然后访问根节点D
步骤4:以D为根节点的树访问完成 对于B这棵树而言 就是其左子树访问完成 要访问右子树E
步骤5:同理 对于E而言 以E为根节点的子树也是一棵树 只不过其左子树和右子树为NULL而已 所以先访问左子树NULL 再访问右子树NULL 然后访问根节点E
步骤6:以E为根节点的树访问完成 对于以B为根节点的树而言 其左右子树访问都完成了 要访问其根节点B 然后对于以A为根节点的树而言 相当于其左子树访问完成 接下来就是访问其右子树C
步骤7:对于以C为根节点的子树而言 也是一棵树 只不过其左子树和右子树为NULL而已 所以先访问左子树NULL 再访问右子树NULL 然后访问根节点C
步骤8:以C为根节点的子树访问完成 对于以A为根节点的树而言 其左右子树均访问完成 就访问其根节点A 然后其后续遍历完成
总结:一直到为空 这样之后 该二叉树就中序遍历完成了 只不过NULL再显示的时候不打印 所以只显示DEBCA
4:层序遍历
A B C D E (NULL) (NULL) (NULL) (NULL) (NULL) (NULL)
步骤1:先访问第一层根节点A 然后再访问第二层根节点 B C
步骤2: 然后访问第三层 根节点 D E 以及以C为根节点的左右空子树 (NULL) (NULL) 其也是作为第三层的根节点 只不过为空
步骤3:然后访问第四层的空根节点(NULL) (NULL) (NULL) (NULL)
总结:一直到为空 层序遍历访问完成 ABCDE
同时可以得到 如果一棵树是完全二叉树 那么其层序遍历 有效数字和NULL一定是分开的
如果不是完全二叉树 则不满足该性质
1.2:二叉树遍历例题
1.某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。该完全二叉树的前序序列为(A)
A ABDHECFG
B ABCDEFGH
C HDBEAFCG
D HDEBFGCA
解析:把ABCDEFGH按照完全二叉树画出来 按照先序遍历一下即可
2.二叉树的先序遍历和中序遍历如下:先序遍历:EFHIGJK;中序遍历:HFIEJKG.则二叉树根结点为(A)
A E
B F
C G
D H
解析:前序遍历一定是先访问以所有数据为一个树的根节点 所以根节点是E
3.设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树先序遍历序列为 ( D )
A adbce
B decab
C debac
D abcde
解析:由后续遍历可知 该树的根节点是a 由根节点是a 然后其中序是b a 可得 以a为根节点 其左子树是一个以b为根节点 其左右子树均为空的树 所以到以a为根节点的右子树 可知 d c e 是一棵树 由中序可知 c是该树的根节点 那么就可以画出该树的二叉树 从而得到先序遍历结果
4.某二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF ,则按层次输出(同一层从左到右)的序列为 (A)
A FEDCBA
B CBAFED
C DEFCBA
D ABCDEF
解析:由后续遍历 得到根节点是F 由于其后续遍历和中序相同 得到以ABCDEF为节点以F为根节点的树没有右子树 同理可以得到 E是以ABCDE为节点的树的根节点 同时以E为根节点的树也没有右子树
那么就可以得到D是以ABCD为节点的树的根节点 依次类推 得到该树是一棵单边树 最终的叶子节点是A 得到其层序遍历是FEDCBA
5.已知某二叉树的前序遍历序列为5 7 4 9 6 2 1,中序遍历序列为4 7 5 6 9 1 2,则其后序遍历序列为( C)
A.4 2 5 7 6 9 1
B.4 2 7 5 6 9 1
C.4 7 6 1 2 9 5
D.4 7 2 9 5 6 1
解析:由前序遍历可得 其根节点是5 并且其紧随的左子树或者右子树有一个是以7为根节点的树 由中序遍历可得 4是以7为根节点的树的左子树 7是以5为根节点的左子树 从而从先序中得到9是以5为跟根节点的右子树的根节点 紧接着 从中序遍历得到 6是以9为根节点的树的左子树 2是以9为根节点的右子树的根节点 从而得到1是以2为根节点的左子树 从而可以得到整棵树 从而得到后续序遍历
6.已知某二叉树的前序遍历序列为ABDEC,中序遍历序列为BDEAC,则该二叉树(C )
A.是满二叉树
B.是完全二叉树,不是满二叉树
C.不是完全二叉树
D.是所有的结点都没有右子树的二叉树
解析:从前序遍历和中序遍历得到 该二叉树以A为根节点 其左子树是一个以B为根节点 DE为节点的树 右子树是一个以C为根节点 C为根节点的树左子树和右子树都为空 但是由中序遍历由B开头又可得以B为根节点的树没有左子树 只有右子树 所以该树不满足完全二叉树
7.一棵非空的二叉树的先序遍历序列与后序遍历序列正好相反,则该二叉树一定满足(C )
A.所有的结点均无左孩子
B.所有的结点均无右孩子
C.只有一个叶子结点
D.至多只有一个结点
解析:由先序遍历和后序遍历相反可得 该树是一个单边树 要么均没有左子树 要么均没有右子树 所以只有C满足
8.如果一颗二叉树的前序遍历的结果是ABCD,则满足条件的不同的二叉树有( B)种
A.13
B.14
C.15
D.16
解析:可得该树是以A为根节点的一棵树 然后由于只有ABCD四个数据 所以该树的高h在3-4之间
罗列之后 得到结果是
三层:
A(B(C,D),()), A((),B(C,D)), A(B(C,()),D), A(B((),C),D),
A(B,C(D,())), A(B,C((),D))
四层:
如果为四层,就是单边树,每一层只有一个节点,除过根节点,其他节点都有两种选择,在上层节点的左边还是右边,所以2*2*2共8种
总共为14种。
1.3:使用代码完成如下一棵树的先序、中序、后续遍历
typedef struct TreeNode//定义一个树的结构体
{
DataType val;
struct TreeNode* _left;//左指针用来指向节点的左子树
struct TreeNode* _right;//右指针用来指向节点的右子树
}TreeNode;
void PrevOrder(TreeNode* ps)//前序遍历
{
if (ps == NULL)//如果指针为空 说明指向的节点不存在 那么直接输出空
{
printf("NULL->");
return;
}
//按照先根节点 再左子树 再右子树的顺序递归遍历
printf("%c->", ps->val);
PrevOrder(ps->_left);
PrevOrder(ps->_right);
}
void InOrder(TreeNode* ps)//中序遍历
{
if (ps == NULL)//如果指针为空 说明指向的节点不存在 那么直接输出空
{
printf("NULL->");
return;
}
//按照先左子树 再根节点 再右子树的顺序递归遍历
InOrder(ps->_left);
printf("%c->", ps->val);
InOrder(ps->_right);
}
void pTailOrder(TreeNode* ps)//后序遍历
{
if (ps == NULL)//如果指针为空 说明指向的节点不存在 那么直接输出空
{
printf("NULL->");
return;
}
//按照先左子树 再右子树 再根节点 的顺序递归遍历
pTailOrder(ps->_left);
pTailOrder(ps->_right);
printf("%c->", ps->val);
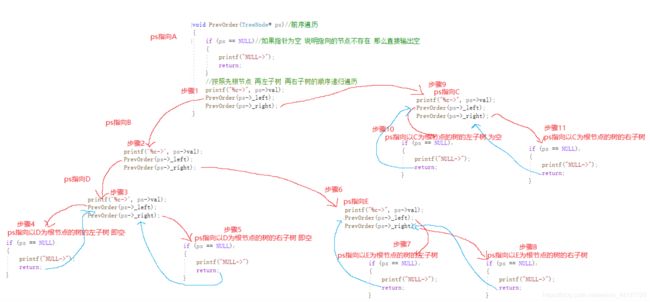
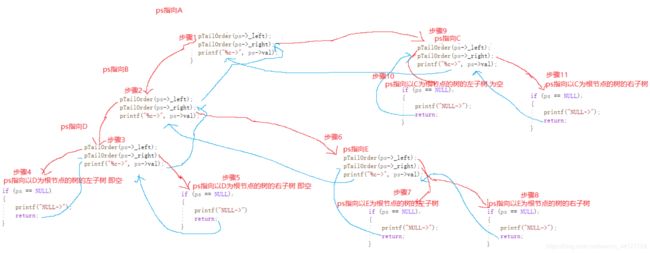
}图解先序遍历:
步骤1:函数开始 ps指针指向节点A 节点A不为空 先输出节点A的值 然后传递节点A的左指针域指向的值即B节点给函数
步骤2:ps指向了节点B 节点B不为空 先输出节点B的值 然后传递节点B的左指针域指向的值即D节点给函数
步骤3:ps指向了节点D 节点D不为空 先输出节点D的值 然后传递节点D的左指针域指向的值即NULL给函数
步骤4:ps指向了NULL 输出NULL 然后结束函数 回到了步骤3 继续执行步骤3的 把D节点的右指针域指向的值即NULL给函数
步骤5:ps指向了NULL 输出NULL 然后结束函数 回到了步骤3 步骤3指向完成 回到步骤2 然后传递节点B的右指针域指向的值即E节点给函数
步骤6:ps指向了节点E 节点E不为空 先输出节点D的值 然后传递节点E的左指针域指向的值即NULL给函数
步骤7:ps指向了NULL 输出NULL 然后结束函数 回到了步骤6 继续执行步骤6的把D节点的右指针域指向的值即NULL给函数
步骤8:ps指向了NULL 输出NULL 然后结束函数 回到了步骤6 步骤6指向完成 回到步骤2 步骤2完成 指向步骤1的把节点A的右指针域指向的值C给函数
步骤9:ps指向了C C所在的节点不为空 先输出C的值 然后传递节点C的左指针域指向的值NULL给函数
步骤10:ps指向了NULL 输出NULL 然后结束函数 回到了步骤9 继续执行步骤 把节点C的右指针域指向的值NULL给函数
步骤11:ps指向了NULL 输出NULL 然后结束函数 回到了步骤9 步骤9结束 返回到步骤1 步骤1结束 函数递归前序遍历完成
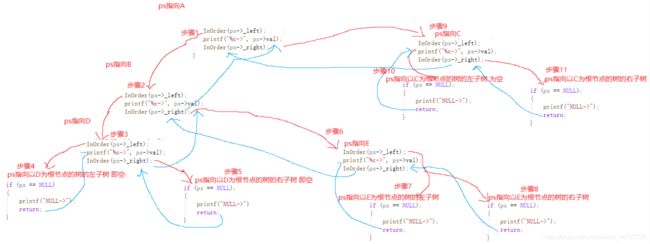
图解中序遍历:
步骤1:函数开始ps指向指向了节点A 节点A不为空 先传递节点A的左指针域指向的值即B节点给函数
步骤2:ps指向了节点B 节点B不为空 先传递节点B的左指针域指向的值即D节点给函数
步骤3:ps指向了节点D 节点D不为空 先传递节点D的左指针域指向的值即NULL给函数
步骤4:ps指向了NULL 输出NULL 结束函数 回到步骤3 然后输出D节点的值 然后继续执行 把D节点的右指针域指向的值即NULL给函数
步骤5:ps指向了NULL 输出NULL 结束函数 回到步骤3 步骤3结束 回到步骤2 输出节点B的值 然后继续执行 把节点B的右指针域指向的值即E给函数
步骤6:ps指向了节点E E不为空 传递节点E左指针域指向的值即NULL给函数
步骤7:ps指向了NULL 输出NULL 结束函数 回到步骤6 然后输出E节点的值 然后继续执行 把E节点的右指针域指向的值即NULL给函数
步骤8:ps指向了NULL 输出NULL 结束函数 回到步骤6 步骤6结束 回到步骤2 步骤2结束 回到步骤1 输出节点A的值 继续执行 把节点A的右指针域指向的值即C传递给函数
步骤9:ps指向了C C不为空 把C节点左指针域所指向的值即NULL给函数
步骤10:ps指向NULL 输出NULL 结束函数 回到步骤9 输出节点C的值 然后继续执行 把C节点的右指针域指向的值即NULL给函数
步骤11:ps指向NULL 输出NULL 结束函数 回到步骤9 步骤9结束 回到步骤1 步骤1结束 函数递归中序遍历完成
图解后序遍历:
步骤1:函数开始ps指向指向了节点A 节点A不为空 先传递节点A的左指针域指向的值即B节点给函数
步骤2:ps指向了节点B 节点B不为空 先传递节点B的左指针域指向的值即D节点给函数
步骤3:ps指向了节点D 节点D不为空 先传递节点D的左指针域指向的值即NULL给函数
步骤4:ps指向了NULL 输出NULL 结束函数 回到步骤3 然后继续执行 把D节点的右指针域指向的值即NULL给函数
步骤5:ps指向了NULL 输出NULL 结束函数 回到步骤3 输出节点D的值 步骤3结束 回到步骤2 然后继续执行 把节点B的右指针域指向的值即E给函数
步骤6:ps指向了节点E E不为空 传递节点E左指针域指向的值即NULL给函数
步骤7:ps指向了NULL 输出NULL 结束函数 回到步骤6 然后继续执行 把E节点的右指针域指向的值即NULL给函数
步骤8:ps指向了NULL 输出NULL 结束函数 回到步骤6 输出节点E的值 步骤6结束 回到步骤2 输出节点B的值 步骤2结束 回到步骤1 继续执行 把节点A的右指针域指向的值即C传递给函数
步骤9:ps指向了C C不为空 把C节点左指针域所指向的值即NULL给函数
步骤10:ps指向NULL 输出NULL 结束函数 回到步骤9 然后继续执行 把C节点的右指针域指向的值即NULL给函数
步骤11:ps指向NULL 输出NULL 结束函数 回到步骤9 输出节点C的值 步骤9结束 回到步骤1 输出节点A的值 步骤1结束 函数递归后序遍历完成
1.4:计算如下二叉树的有效节点个数和叶子节点个数
int SizeTreeList(TreeNode* ps)//计算树中的有效节点个数
{
if (ps == NULL)
return 0;
return 1 + SizeTreeList(ps->_left) + SizeTreeList(ps->_right);
}
int SizeTreeListLeaf(TreeNode* ps)//计算树中叶子节点的个数
{
//叶子节点一定没有左子树和右子树
if (ps == NULL)
return 0;
if (ps->_left == NULL && ps->_right == NULL)
return 1;
return 0+ SizeTreeListLeaf(ps->_left) + SizeTreeListLeaf(ps->_right);
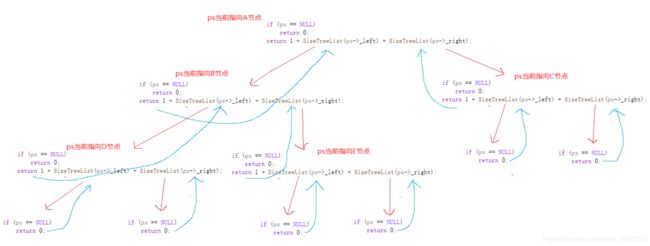
}图解:计算树的有效节点个数
步骤1:函数开始ps指向节点A 节点A不为空 把节点A的左指针域指向的值即B节点传递给函数
步骤2:ps指向节点B 节点B不为空 把节点B的左指针域指向的值即节点D传递给函数
步骤3:ps指向节点D 节点D不为空 把节点D的左指针域指向的值即NULL传递给函数
步骤4:ps指向NULL 步骤4结束 返回0 到步骤3 把节点D的右指针域指向的值NULL传递给函数
步骤5:ps指向NULL 步骤5结束 返回0 到步骤3 步骤3返回1+0+0即1返回到步骤2 步骤2继续执行把节点B的右指针域指向的值即E节点传递给函数
步骤6:ps指向节点E 节点E不为空 把节点E的左指针域指向的值即NULL传递给函数
步骤7:ps指向NULL 步骤7结束 返回0 到步骤6 把节点E的右指针域指向的值NULL传递给函数
步骤8:ps指向NULL 步骤8结束 返回0 到步骤6 步骤6 返回1+0+0即1到步骤2 步骤2结束 返回1+1+1即3到步骤1 步骤1 继续执行 把节点A的右指针域指向的值即C节点传递给函数
步骤9:ps指向节点C 节点C不为空 把节点C的左指针与指向的值即NULL传递给函数
步骤10:ps指向NULL 步骤10结束 返回0到步骤9 步骤9继续指向 把节点C的右指针域指向的值即NULL传递给函数
步骤11:ps指向NULL 步骤11结束 返回0到步骤9 步骤9结束 返回1+0+0到步骤1 步骤1结束 返回1+3+1即5 那么该树的有效节点个数是5
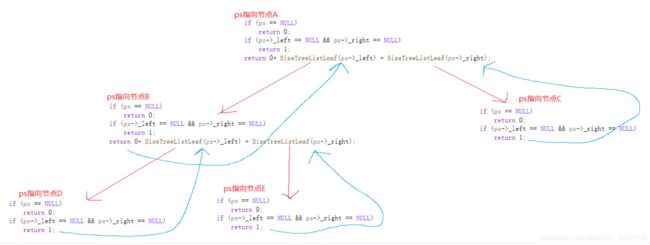
图解:计算树的叶子节点个数
步骤1:函数开始ps指向节点A 节点A不为空 并且节点A的左指针域和右指针域所指向的值都不为空
把节点A的左指针域的值即节点B传递给函数
步骤2:ps指向节点B 节点B不为空 并且节点B的左指针域和右指针域所指向的值都不为空 把节点B的左指针域指向的值即节点D传递给函数
步骤3:ps指向节点D 节点D不为空 但是节点D的左指针域和右指针域所指向的值都是空 步骤3结束 返回1到步骤2 步骤2继续执行 把节点B的右指针域指向的值即E传递给函数
步骤4:ps指向节点E 节点E不为空 但是节点E的左指针域和右指针域所指向的值都是空 步骤4结束 返回1到步骤2 步骤2结束 返回0+1=1即2到步骤1 步骤1继续执行 把节点A的右指针域指向的值即节点C传递给函数
步骤5:ps指向节点C 节点C不为空 但是节点C的左指针域和右指针域所指向的值都是空 步骤5结束 返回1到步骤1 步骤1结束 返回2+1即3 那么该树的叶子节点个数是3
1.9:二叉树OJ题目
例题1:给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
要求将前序遍历的值放到一个数组中 并返回该数组的首地址
int SizeTree(struct TreeNode* root)//计算树的有效值个数
{
if (root == NULL)
return 0;
return 1 + SizeTree(root->left) + SizeTree(root->right);
}
void PrevOrder(struct TreeNode* root, int* Arr, int* i)//前序遍历
{
if (root == NULL)
return;
//按照前序遍历的顺序 每次把前序遍历的值存放到数组中的去 要注意的一点是 这里的i是要传址 不是传值
Arr[*i] = root->val;
(*i)++;
PrevOrder(root->left, Arr, i);
PrevOrder(root->right, Arr, i);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize)
{
int Size = SizeTree(root);//调用函数 得到树的有效节点个数 从而去开辟数组
int* NewArr = (int*)malloc(sizeof(int) * Size);//动态开辟一个树有效节点个数大小的数组
if (NewArr == NULL)
{
exit(-1);
}
int i = 0;
PrevOrder(root, NewArr, &i);//调用前序遍历函数 把树节点的值按照前序遍历的顺序把值放到数组中
*returnSize = Size;//返回数组的有效元素个数
return NewArr;//返回数组首地址
}解析:跟使用递归调用前序遍历的原理相同 只不过 我们之前是按照前序遍历的顺序打印出树的值
这次是按照前序遍历的顺序把值放到数组中
尤其是要注意的是 一定要传递i的地址 而不是传值 不然每次递归调用结束 返回的时候 i的值都是处在原来函数中i的值的大小 这样数组中部分值就会被其他的树节点该覆盖了
例题2:给你二叉树的根节点 root ,返回它节点值的 中序 遍历。
要求将中序遍历的值放到一个数组中 并返回该数组的首地址
int SizeTree(struct TreeNode* root)//计算树的有效值个数
{
if (root == NULL)
return 0;
return 1 + SizeTree(root->left) + SizeTree(root->right);
}
void MiddleOrder(struct TreeNode* root, int* Arr, int* i)//中序遍历
{
if (root == NULL)
return;
//按照中序遍历的顺序 每次把中序遍历的值存放到数组中的去 要注意的一点是 这里的i是要传址 不是传值
MiddleOrder(root->left, Arr, i);
Arr[*i] = root->val;
(*i)++;
MiddleOrder(root->right, Arr, i);
}
int* inorderTraversal(struct TreeNode* root, int* returnSize)
{
int Size = SizeTree(root);//调用函数 得到树的有效节点个数 从而去开辟数组
int* NewArr = (int*)malloc(sizeof(int) * Size);//动态开辟一个树有效节点个数大小的数组
if (NewArr == NULL)
{
exit(-1);
}
int i = 0;
MiddleOrder(root, NewArr, &i);//调用中序遍历函数 把树节点的值按照中序遍历的顺序把值放到数组中
*returnSize = Size;//返回数组的有效元素个数
return NewArr;//返回数组首地址
}解析:同例题1
例题3:给你二叉树的根节点 root ,返回它节点值的 后序 遍历。
要求将后序遍历的值放到一个数组中 并返回该数组的首地址
int SizeTree(struct TreeNode* root)//计算树的有效值个数
{
if (root == NULL)
return 0;
return 1 + SizeTree(root->left) + SizeTree(root->right);
}
void pTailOrder(struct TreeNode* root, int* Arr, int* i)//后序遍历
{
if (root == NULL)
return;
//按照后序遍历的顺序 每次把后序遍历的值存放到数组中的去 要注意的一点是 这里的i是要传址 不是传值
pTailOrder(root->left, Arr, i);
pTailOrder(root->right, Arr, i);
Arr[*i] = root->val;
(*i)++;
}
int* postorderTraversal(struct TreeNode* root, int* returnSize)
{
int Size = SizeTree(root);//调用函数 得到树的有效节点个数 从而去开辟数组
int* NewArr = (int*)malloc(sizeof(int) * Size);//动态开辟一个树有效节点个数大小的数组
if (NewArr == NULL)
{
exit(-1);
}
int i = 0;
pTailOrder(root, NewArr, &i);//调用后序遍历函数 把树节点的值按照后序遍历的顺序把值放到数组中
*returnSize = Size;//返回数组的有效元素个数
return NewArr;//返回数组首地址
}解析:同例题1
例题4:如果二叉树每个节点都具有相同的值,那么该二叉树就是单值二叉树。
只有给定的树是单值二叉树时,才返回 true;否则返回 false。
int pTailOrder(struct TreeNode* root, int val)//遍历对比
{
if (root == NULL)//如果节点等于空 返回0
return 0;
if (root->val == val)//如果节点的值等于val 那么递归
{
return pTailOrder(root->left, val) + pTailOrder(root->right, val);
}
else//不相等就返回1
{
return 1;
}
}
bool isUnivalTree(struct TreeNode* root)
{
if(root == NULL)//如果树等于空 那么直接返回true
return true;
int val = root->val;//定义一个val保存该树根节点的值
if(pTailOrder(root, val) > 0)//判断遍历之后函数的返回值是否大于0 大于说明树节点值不全相同
{
return false;
}
else
{
return true;
}
}解析:如果该树是单值树 那么最终的返回结果一定是0 如果存在某个节点不等于val 那么最终的结果一定是大于0的 对于该类问题 还是拆分成左子树 右子树 计算最好
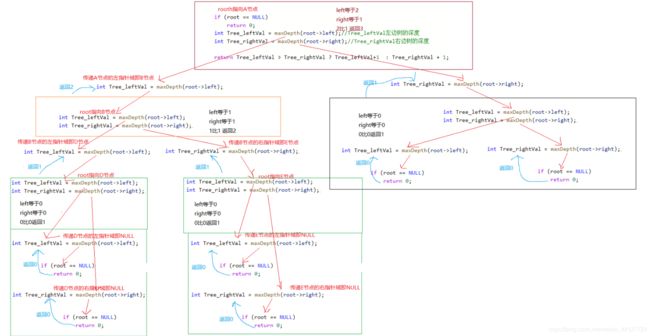
例题5:给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
示例:
int maxDepth(struct TreeNode* root)
{
if (root == NULL)
return 0;
int Tree_leftVal = maxDepth(root->left);//Tree_leftVal左边树的深度
int Tree_rightVal = maxDepth(root->right);//Tree_rightVal右边树的深度
return Tree_leftVal > Tree_rightVal ? Tree_leftVal+1 : Tree_rightVal + 1;
//如果左边树的深度大于右边树的深度 那么结果是左边树的深度+1 反之是右边树的深度+1
}图解:
步骤1:函数开始root指针指向节点A 节点A不为空 把节点A的左指针域的值即节点B传递给函数
步骤2:root指向节点B 节点B不为空 把节点B的左指针域的值即节点D传递给函数
步骤3:root指向节点D 节点D不为空 把节点D的左指针域的值即NULL传递给函数
步骤4:root指向为空 返回0 步骤4结束 在步骤3中定义的Tree_leftVal等于返回值0
即Tree_leftVal = 0 把D节点的右指针域的值即NULL传递给函数
步骤5:root指向为空 返回0 步骤5结束 在步骤3中定义的Tree_rightVal等于返回值0
即Tree_rightVal = 0 然后判断步骤3中Tree_leftVal Tree_rightVal的大小 因为0不大于0 所以返回1步骤3结束 返回1到步骤2 在步骤2中定义的Tree_leftVal等于1 即Tree_leftVal = 1然后 把B节点的右指针域的值即E节点传递给函数
步骤6:root指向节点E 节点E不为空 把节点E的左指针域的值即NULL传递给函数
步骤7:root指向为空 返回0 步骤7结束 在步骤6中定义的Tree_leftVal等于返回值0
即Tree_leftVal = 0 把E节点的右指针域的值即NULL传递给函数
步骤8:root指向为空 返回0 步骤8结束 在步骤6中定义的Tree_rightVal等于返回值0
即Tree_rightVal = 0 然后判断步骤6中Tree_leftVal Tree_rightVal的大小 因为0不大于0 所以返回1步骤6结束 返回1到步骤2 在步骤2中定义的Tree_rightVal等于1 即Tree_rightVal = 1 然后判断步骤2中的Tree_leftVal Tree_rightVal的大小 因为1不大于1 所以返回2 步骤2结束, 到步骤1 步骤1中定义的Tree_leftVal等于2 然后把节点A的右指针域的值即节点C传递给函数
步骤9:root指向节点C 节点C不为空 把节点C的左指针域的值即NULL传递给函数
步骤10:root指向为空 返回0 步骤10结束 在步骤9中定义的Tree_leftVal等于返回值0
即Tree_leftVal = 0 把C节点的右指针域的值即NULL传递给函数
步骤11:root指向为空 返回0 步骤11结束 在步骤9中定义的Tree_rightVal等于返回值0
即Tree_rightVal = 0 然后判断步骤9中Tree_leftVal Tree_rightVal的大小 因为0不大于0 所以返回1 步骤9结束 返回到步骤1 在步骤1中定义的Tree_rightVal等于返回值1
即Tree_rightVal = 1
步骤12:判断步骤1中的Tree_leftVal Tree_rightVal的大小 因为2大于1 所以返回3 函数结束那么该树的深度就是3
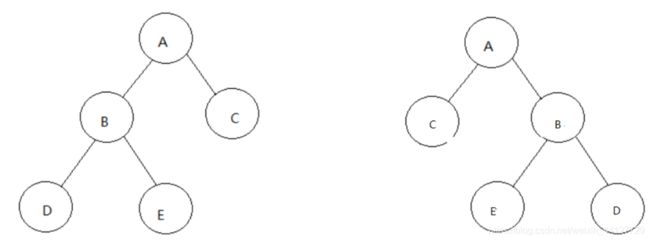
例题6:反转一个二叉树(也叫二叉树的镜像)
//方法1
struct TreeNode* mirrorTree(struct TreeNode* root)
{
if(root == NULL)//如果根节点为空 那么不需要交换 直接返回
return NULL;
struct TreeNode*p1 = mirrorTree(root->left);//p1存放当前节点左子树节点的值
struct TreeNode*p2 = mirrorTree(root->right);//p2存放当前节点右子树节点的值
root->left = p2;//当前节点的左指针域指向当前节点右指针域的值
root->right = p1;//当前节点的右指针域指向当前节点左指针域的值
return root;
}
//方法2
struct TreeNode* mirrorTree(struct TreeNode* root)
{
if (root == NULL)//如果根节点为空 那么不需要交换 直接返回
return NULL;
//先进行互换
struct TreeNode*tmp = root->left;
root->left = root->right;
root->right = tmp;
//从互换之后再开始往下继续遍历
mirrorTree(root->left);
mirrorTree(root->right);
return root;
}解析方法1:
步骤1:函数开始root指向节点A 节点A不为空 把节点A的左指针域的值即B节点传递给函数
步骤2:root指向节点B 节点B不为空 把节点B的左指针域的值即节点D传递给函数
步骤3:root指向节点D 节点D不为空 把节点D的左指针域的值传递给函数
步骤4:root指向NULL 返回NULL 步骤4结束 返回步骤3 在步骤3中 定义P1接收步骤4返回的节点D的左指针域的值NULL, 步骤3继续执行 把节点D的右指针域指向的值即NULL传递给函数
步骤5:root指向NULL 返回NULL 步骤5结束 返回步骤3 在步骤3中 定义P2接收步骤5返回的节点D的右指针值NULL,继续执行步骤3 节点D的左指针root->left指向节点D的右指针域的值 节点D的右指针root->right指向节点D的左指针域的值,步骤3结束,返回指向节点D的指针,回到步骤2 在步骤2中定义了p1接收步骤3返回的节点D的指针 然后继续指向 把节点B的右指针域的值即E节点传递给函数
步骤6:root指向了E节点 E节点不为空 把E节点的左指针域的值即NULL传递给函数
步骤7:root指向NULL 返回NULL 步骤7结束 在步骤6中定义p1接收步骤7返回的值NULL 继续执行步骤6 把E节点的右指针域指向的值即NULL传递给函数
步骤8:root指向NULL 返回NULL 步骤8结束 在步骤6中定义p2接收步骤8中返回的值NULL 继续指向步骤6 节点E的左指针root->left指向节点E的右指针域的值 节点E的右指针root->right指向节点E的左指针域的值, 步骤6结束 返回指向节点E的指针,回到步骤2 在步骤2中定义了p2接收步骤6中返回的节点E的指针 然后步骤2的root指针即节点B的左指针root->left指向节点B的右指针域的值即E 节点B的右指针root->right指向节点B的左指针域的值即D 然后步骤2结束 返回指向节点B的指针 返回步骤1 在步骤1中定义了p1接收步骤2中的返回值即指向节点B的指针 继续执行步骤1 把节点A的右指针域的值即C节点传递给函数
步骤9:root指向节点C 节点C不为空 把节点C的左指针域的值传递给函数
步骤10:root指向NULL 返回NULL 步骤10结束 返回步骤9 在步骤9中 定义P1接收步骤10返回的节点C的左指针域的值NULL, 步骤9继续执行 把节点C的右指针域指向的值即NULL传递给函数
步骤11:root指向NULL 返回NULL 步骤11结束 返回步骤9 在步骤9中 定义p2接收步骤11返回的节点C的右指针域的值NULL, 步骤9继续执行 节点C的左指针root->left指向节点C的右指针域的值即NULL 节点C的右指针root->right指向节点C的左指针域的值即NULL 步骤9结束 返回指向当前root的指针即指向节点C的指针 返回步骤1 在步骤1中 定义了p2接收步骤9中的返回值即指向节点C的指针 继续执行步骤1 节点A的左指针root->left指向节点A的右指针域的值即C节点 节点A的右指针root->right指向节点A的左指针域的值即B节点
步骤12:全部调用完毕 返回root指针
例题7:
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
//从结构上判断 两者的结构是否相同
if(p == NULL && q == NULL)
return true;
if((p == NULL && q != NULL) || (p != NULL && q == NULL))
return false;
//如果p当前指向是已经空了 但是q并不为空 或者相反那么结构上就是不同
//从值上判断
if((p->val) != (q->val))
{
return false;
}
else
{
return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
//最终的返回结果是两者想与的结果 也就是从根节点开始 左右两子树结构和值上都相等
}
}例题8:
给定两个非空二叉树 s 和 t,检验 s 中是否包含和 t 具有相同结构和节点值的子树。s 的一个子树包括 s 的一个节点和这个节点的所有子孙。s 也可以看做它自身的一棵子树。
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
//从结构上判断 两者的结构是否相同
if (p == NULL && q == NULL)
return true;
if ((p == NULL && q != NULL) || (p != NULL && q == NULL))
return false;
//从值上判断
if ((p->val) != (q->val))
{
return false;
}
else
{
return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
//最终的返回结果是两者想与的结果 也就是从根节点开始 左右两子树结构和值上都相等
}
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{
if (root == NULL)//如果root是空 那就没有可比性 直接错误
return false;
if (isSameTree(root, subRoot))//如果root从一开始就和sub树相同 并且满足相等 就返回true
{
return true;
}
else//如果root根节点和sub树根节点不同 那么从root的左右子树与其相比较
{
return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}
}解析:
步骤1:函数一开始先判断传入的参数root是否为空 如果为空 那么就不能相比较 所以直接返回false
步骤2:步骤1不成立 继续往下执行 判断当前root树从根节点开始和sub树比较 是否相同 如果不同
执行下一步 如果相同 直接返回true
步骤3:如果步骤2不成立 也就是说root从树根节点开始和sub树不相同 所以我们从root的左子树的根节点开始比较 如果左子树存在 那么返回true 如果不存在 返回false 然后从root根节点的右子树进行比较 只要从根节点左右子树一直遍历 有一个从结构和值上都相同的子树和sub树相同 都成立 都返回true
例题9:
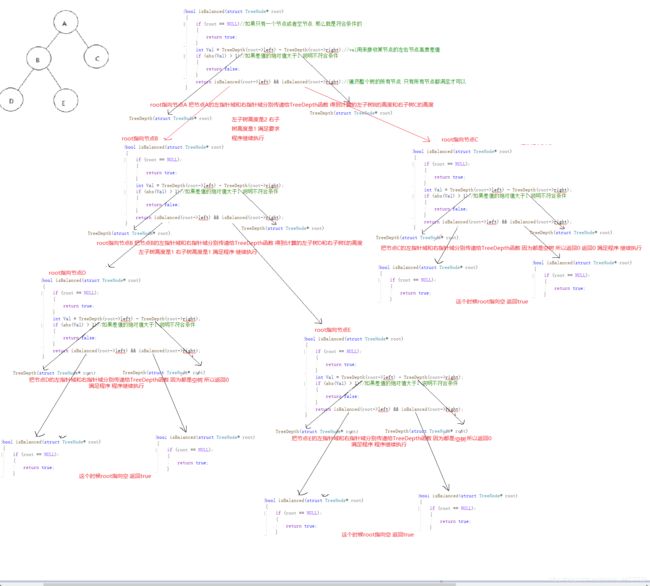
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
//方法1 时间复杂度最好是O(N) 最坏是O(N^2)
int TreeDepth(struct TreeNode* root)//求某个节点层次
{
if (root == NULL)
{
return 0;
}
int leftDepth = TreeDepth(root->left);
int rightDepth = TreeDepth(root->right);
return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}
bool isBalanced(struct TreeNode* root)
{
if (root == NULL)//如果只有一个节点或者空节点 那么就是符合条件的
{
return true;
}
int Val = TreeDepth(root->left) - TreeDepth(root->right);//val用来接收某节点的左右节点高度差值
if (abs(Val) > 1)//如果差值的绝对值大于1 说明不符合条件
{
return false;
}
return isBalanced(root->left) && isBalanced(root->right);//遍历整个树的所有节点 只有所有节点都满足才可以
}
//方法2 时间复杂度O(N)
bool _isBalanced(struct TreeNode* root, int* hight)
{
if (root == NULL)//如果root指向为空 那么高度为0 并且返回true
{
*hight = 0;
return true;
}
else//否则 判断左/右子树是否等于false 如果左子树和右子树的高度大于1 返回false 否则 返回最终的高度和true
{
int leftVal = 0;
if (_isBalanced(root->left, &leftVal) == false)
{
return false;
}
int rightVal = 0;
if (_isBalanced(root->right, &rightVal) == false)
{
return false;
}
if (abs(leftVal - rightVal) > 1)
{
return false;
}
*hight = (leftVal > rightVal ? leftVal + 1 : rightVal + 1);
return true;
}
}
bool isBalanced(struct TreeNode* root)
{
int hight = 0;
return _isBalanced(root, &hight);
}图解方法1:
步骤1:程序一开始 root指针指向了节点A 节点A不为空 定义了一个变量Val 把节点A的左指针域和右指针域的值传递给TreeDepth函数 得到节点B和节点C的高度 分别是2和1 然后得到Val变量的绝对值等于1 跳过if 程序继续执行 把节点A的左指针域即节点B传给isBalanced函数
步骤2:root指向节点B 节点B不为空 把节点B的左指针域的值和右指针域的值传递给TreeDepth函数 得到节点D和节点E的高度 分别是1和1 然后得到Val变量的绝对值等于0 跳过if 程序继续执行 把节点B的左指针域的值即NULL 和节点E的左指针域的值即NULL传递给isBalanced函数
步骤3:root指向节点B的左指针域的值即NULL 返回true 步骤3结束
步骤4:root指向节点B的右指针域的值即NULL 返回true 步骤4结束
步骤5:步骤3和4结束 步骤5得到两者的返回值true 两者想与之后得到步骤2的结果是true 步骤2结束 返回步骤1 步骤1的 isBalanced(root->left)为true 把节点A的右指针域即节点C传给isBalanced函数
步骤6:root指向节点C 节点C不为空 把节点C的左指针域的值即NULL和右指针域的值即NULL传递给TreeDepth函数 返回0 因为0-0的绝对值小于1 所以跳过if 把节点C的左指针域和右指针域的值NULL传给isBalanced函数
步骤7:节点C的左指针域为空 返回true
步骤8:节点C的右指针域为空 返回true
步骤9:步骤7、8结束 true相与 得到true 步骤6得到返回的true 步骤6结束 返回给步骤1 步骤1的isBalanced(root->right)为true和 isBalanced(root->left)相与 得到true 函数结束 该树满足平衡二叉树
图解方法2:
相比方法1,方法2在时间复杂度上是优于方法2的 方法1存在太多的重复计算 每传递一个节点 都会从该节点开始 遍历以该节点作为根节点的所有节点 所以每次都会重复计算很多节点 相比较之下 方法二从根节点开始向上遍历 每次计算完通过指针传递的方式把高度返回给上一个函数 然后把true或者flase结果返回给上一个函数 在上一个函数中进行判断 少了冗余的计算
例题10:
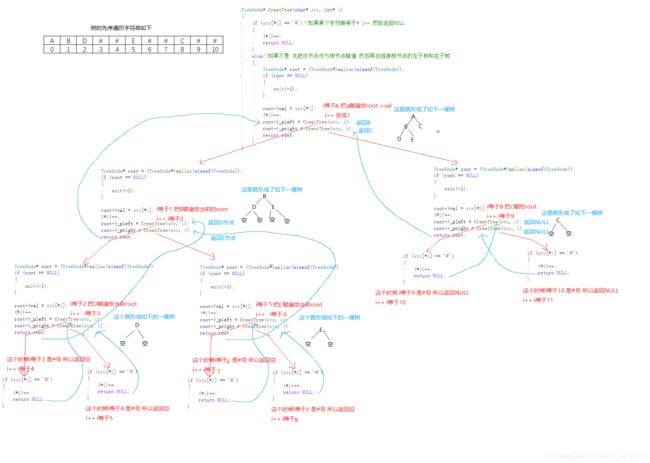
编一个程序,读入用户输入的一串先序遍历字符串,根据此字符串建立一个二叉树(以指针方式存储)。 例如如下的先序遍历字符串: ABC##DE#G##F### 其中“#”表示的是空格,空格字符代表空树。建立起此二叉树以后,再对二叉树进行中序遍历,输出遍历结果。
输入描述:
输入包括1行字符串,长度不超过100。
输出描述:
可能有多组测试数据,对于每组数据, 输出将输入字符串建立二叉树后中序遍历的序列,每个字符后面都有一个空格。 每个输出结果占一行。
# include
# include
typedef struct TreeNode//定义一个树的结构体
{
char val;
struct TreeNode *_pleft;//节点的左指针域
struct TreeNode *_pright;//节点的右指针域
}TreeNode;
TreeNode * CreatTree (char *str, int *i)
{
if(str[*i] == '#')//如果某个字符串等于# i++ 然后返回NULL
{
(*i)++;
return NULL;
}
else//如果不是 先把该节点作为根节点赋值 然后再去链接根节点的左子树和右子树
{
TreeNode*root = (TreeNode*)malloc(sizeof(TreeNode));
if(root == NULL)
{
exit(-1);
}
root->val = str[*i];
(*i)++;
root->_pleft = CreatTree(str, i);
root->_pright = CreatTree(str, i);
return root;
}
}
void InOrder (TreeNode*pst)//树的中序遍历
{
if(pst == NULL)
{
return;
}
InOrder(pst->_pleft);
printf ("%c ", pst->val);
InOrder(pst->_pright);
}
int main (void)
{
char str[100] = {0};
scanf("%s", str);//输入一个先序遍历的字符串
int i = 0;//字符串的坐标i
TreeNode *pTree = CreatTree(str, &i);//把字符串的地址和首坐标传入
InOrder(pTree);
return 0;
} 图解如下
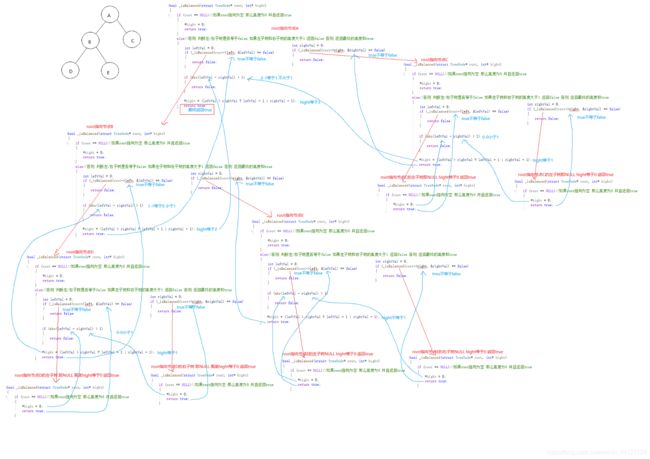
例题11:计算二叉树第k层有多少个节点
#if 0
//计算二叉树第k层节点个数 方法1 时间复杂度O(N)
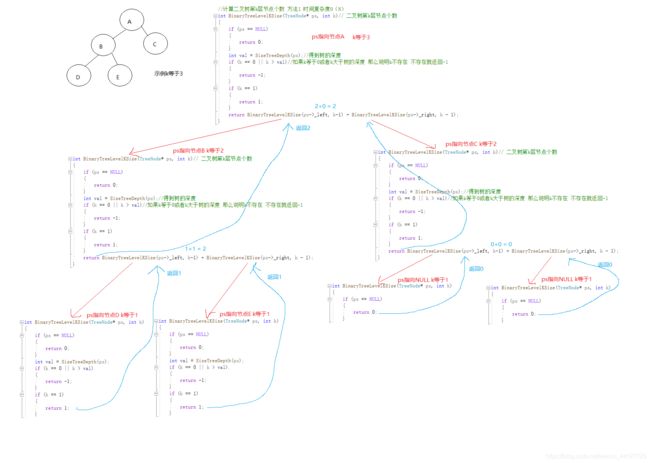
int BinaryTreeLevelKSize(TreeNode* ps, int k)// 二叉树第k层节点个数
{
if (ps == NULL)
{
return 0;
}
int val = SizeTreeDepth(ps);//得到树的深度
if (k == 0 || k > val)//如果k等于0或者k大于树的深度 那么说明k不存在 不存在就返回-1
{
return -1;
}
if (k == 1)
{
return 1;
}
return BinaryTreeLevelKSize(ps->_left, k-1) + BinaryTreeLevelKSize(ps->_right, k - 1);
}
#endif
//方法2
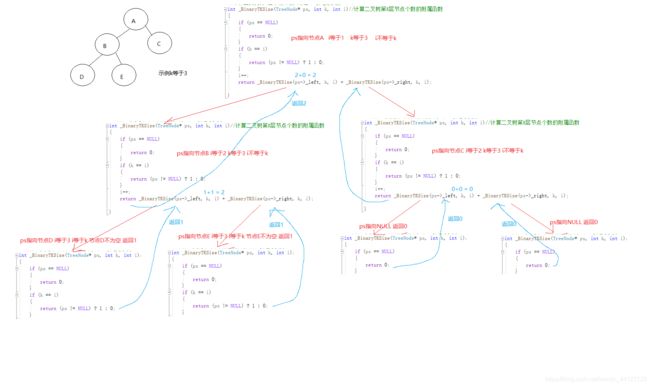
int _BinaryTKSize(TreeNode* ps, int k, int i)//计算二叉树第K层节点个数的附属函数
{
if (ps == NULL)
{
return 0;
}
if (k == i)
{
return (ps != NULL) ? 1 : 0;
}
i++;
return _BinaryTKSize(ps->_left, k, i) + _BinaryTKSize(ps->_right, k, i);
}
int BinaryTreeLevelKSize(TreeNode* ps, int k)// 二叉树第k层节点个数
{
int i = 1;
int val = SizeTreeDepth(ps);//得到树的深度
if (k == 0 || k > val)//如果k等于0或者k大于树的深度 那么说明k不存在 不存在就返回-1
{
return -1;
}
return _BinaryTKSize(ps, k, i);//调用附属函数
}方法1图解如下:
例题12:查找二叉树中值为x的节点
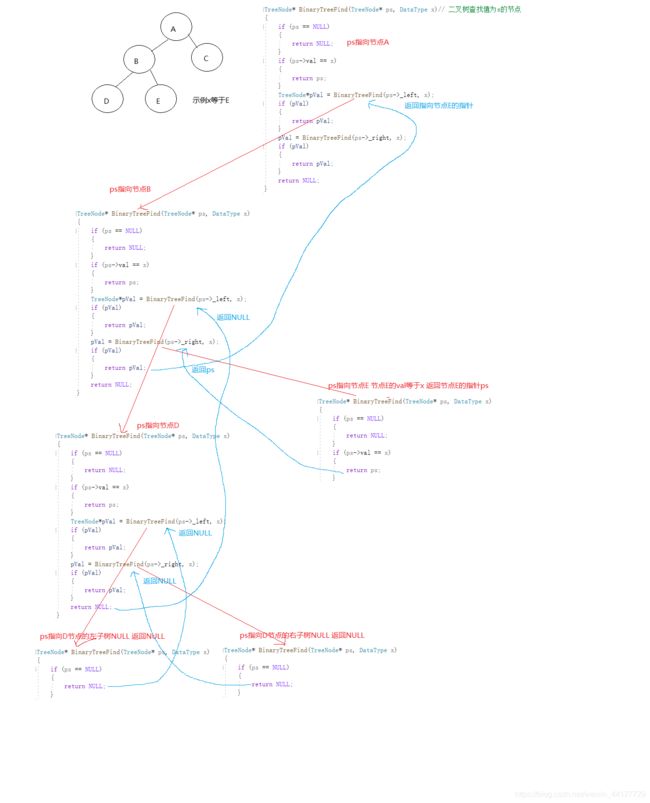
TreeNode* BinaryTreeFind(TreeNode* ps, DataType x)// 二叉树查找值为x的节点
{
if (ps == NULL)
{
return NULL;
}
if (ps->val == x)
{
return ps;
}
TreeNode*pVal = BinaryTreeFind(ps->_left, x);
if (pVal)
{
return pVal;
}
pVal = BinaryTreeFind(ps->_right, x);
if (pVal)
{
return pVal;
}
return NULL;
}图解如下:
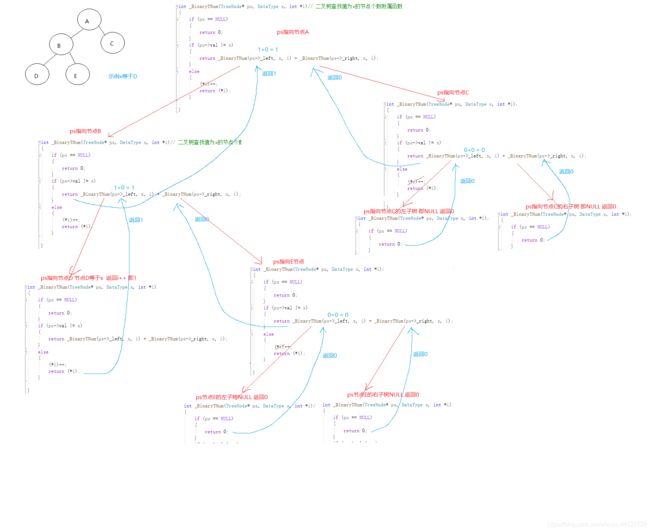
例题13:查找二叉树中值为x的节点有多少个
int _BinaryTNum(TreeNode* ps, DataType x, int *i)// 二叉树查找值为x的节点个数附属函数
{
if (ps == NULL)
{
return 0;
}
if (ps->val != x)
{
return _BinaryTNum(ps->_left, x, i) + _BinaryTNum(ps->_right, x, i);
}
else
{
(*i)++;
return (*i);
}
}
int BinaryTreeNum(TreeNode* ps, DataType x)// 二叉树查找值为x的节点个数
{
int i = 0;
return _BinaryTNum(ps, x, &i);
}图解如下:
例题14:二叉树的层序遍历
//附带队列函数
typedef TreeNode* TNDataType;
//这一点很重要 也就是队列中存储的数据是树节点的指针类型
typedef struct QueenNode
{
TNDataType val;
struct QueenNode* pNext;
}QueenNode;
typedef struct Queen
{
QueenNode* prev;
QueenNode* pTail;
}Queen;
/* 队列的接口函数 */
void InitQueen(Queen*pst);//队列的初始化
void QueenPush(Queen*pst, TNDataType ps);//入队
void QueenPop(Queen* pst);//出队
TNDataType QueenpTop(Queen* pst);//出队头的数据
bool EmptyQueen(Queen*pst);//判断队列是否为空
void DestoryQueen(Queen*pst);//销毁队列
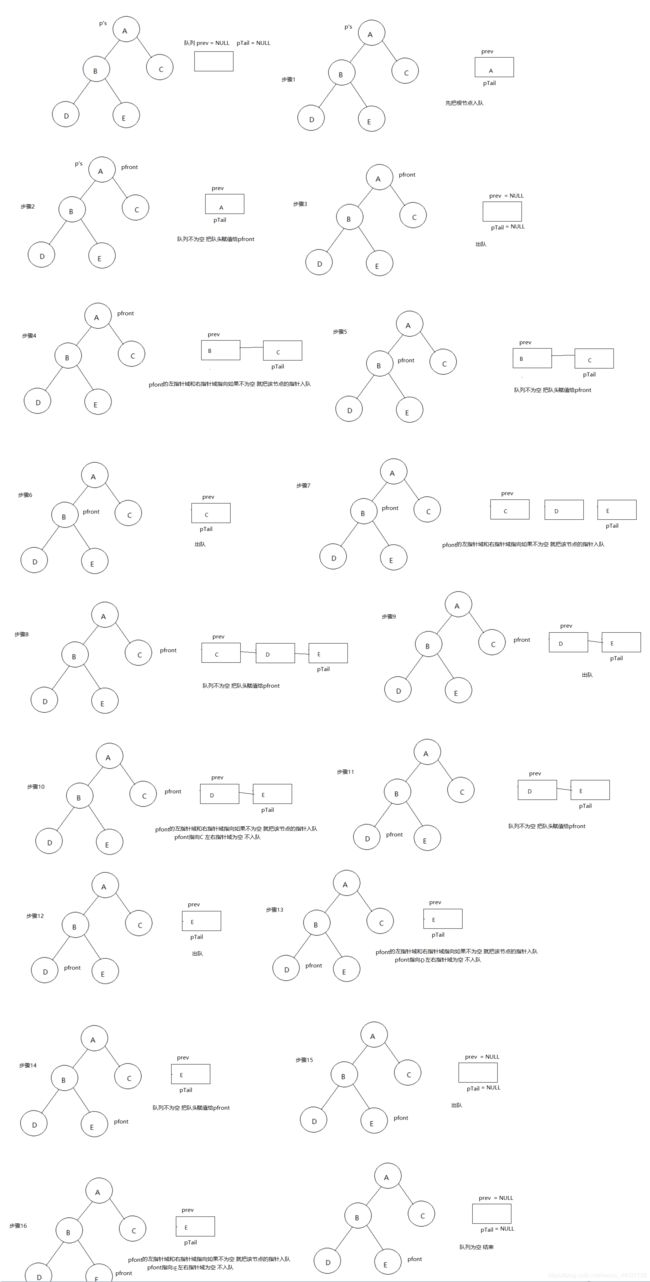
void BinaryTreeLevelOrder(TreeNode* ps)// 层序遍历
{
Queen pst;
InitQueen(&pst);
if (ps == NULL)//如果指针为空 说明指向的节点不存在 那么直接输出空
{
printf("NULL->");
return;
}
QueenPush(&pst, ps);
while (!(EmptyQueen(&pst)))//如果队列不为空
{
TNDataType pfront = QueenpTop(&pst);//获取队头数据
QueenPop(&pst);
printf("%c->", pfront->val);
if (pfront->_left != NULL)
{
QueenPush(&pst, pfront->_left);
}
if (pfront->_right != NULL)
{
QueenPush(&pst, pfront->_right);
}
}
}图解如下:
例题15:判断一个树是不是完全二叉树
//附带队列函数
typedef TreeNode* TNDataType;
//这一点很重要 也就是队列中存储的数据是树节点的指针类型
typedef struct QueenNode
{
TNDataType val;
struct QueenNode* pNext;
}QueenNode;
typedef struct Queen
{
QueenNode* prev;
QueenNode* pTail;
}Queen;
/* 队列的接口函数 */
void InitQueen(Queen*pst);//队列的初始化
void QueenPush(Queen*pst, TNDataType ps);//入队
void QueenPop(Queen* pst);//出队
TNDataType QueenpTop(Queen* pst);//出队头的数据
bool EmptyQueen(Queen*pst);//判断队列是否为空
void DestoryQueen(Queen*pst);//销毁队列
int BinaryTreeComplete(TreeNode* ps)// 判断二叉树是否是完全二叉树
{
Queen pst;
InitQueen(&pst);
if (ps == NULL)//如果指针为空 说明是空树 空树也是完全二叉树 返回1
{
return 1;
}
QueenPush(&pst, ps);
while (!(EmptyQueen(&pst)))
{
TNDataType pfront = QueenpTop(&pst);//获取队头数据
QueenPop(&pst);
if (pfront == NULL)//如果出队的元素为空 则结束循环
{
break;
}
QueenPush(&pst, pfront->_left);
QueenPush(&pst, pfront->_right);
}
while (!(EmptyQueen(&pst)))//如果队列中剩余的元素中存在非空元素 那么该树就不是完全二叉树
{
TNDataType pfront = QueenpTop(&pst);//获取队头数据
QueenPop(&pst);
if (pfront != NULL)
{
return 0;
}
}
return 1;
}
解析:完全二叉树有一个性质是二叉树不具有的 如果一棵树是完全二叉树 那么其层序遍历 有效数字和NULL一定是分开的 如果不是完全二叉树 则不满足该性质
示例:
树1的层序遍历是 ABCDE NULL NULL NULL NULL NULL NULL
树2的层序遍历是 ABC NULL NULL E NULL NULL NULL NULL
例题16:给定一个二叉树,检查它是否是镜像对称的。
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
//从结构上判断 两者的结构是否相同
if (p == NULL && q == NULL)
return true;
if ((p == NULL && q != NULL) || (p != NULL && q == NULL))
return false;
//如果p当前指向是已经空了 但是q并不为空 或者相反那么结构上就是不同
//从值上判断
if ((p->val) != (q->val))
{
return false;
}
else
{
return isSameTree(p->left, q->right) && isSameTree(p->right, q->left);
//最终的返回结果是两者想与的结果 也就是从根节点开始 左右两子树结构和值上都相等
}
}
bool isSymmetric(struct TreeNode* root)
{
if (root == NULL)
{
return true;
}
return isSameTree(root->left, root->right);
}
解析:一棵树是对称二叉树 那么他的镜像就要是一摸一样的 那么这棵树的左右子树一定是相同的 依据该特性 改写一下判断一棵树和另一棵树是否相同即可