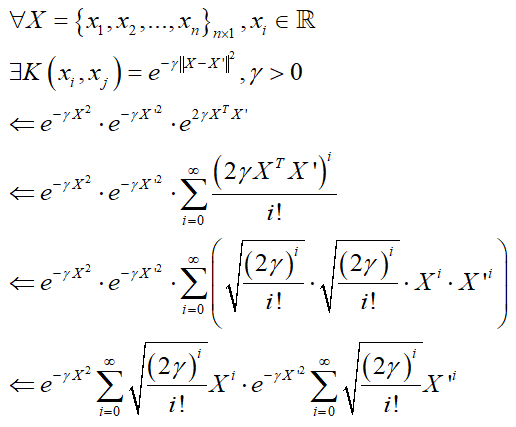返回主页
4 核函数理解
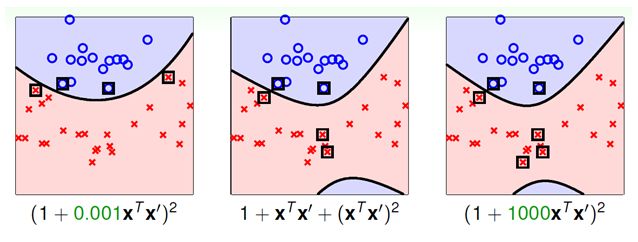
4.1 多项式核函数(Polynomial kernel function)及其推演
注:当 zeta = 0; gamma = 1; degree = 1 时,即为线性核函数
4.2 高斯核函数(Gaussian kernel)及其推演
4.3 手写 SVM 算法并与 Sklearn 作比较
# -*- coding: utf-8 -*-
from __future__ import (absolute_import, division, print_function)
import numpy as np
import pandas as pd
import scipy.spatial.distance as dist
from sklearn.utils import shuffle
from sklearn.model_selection import train_test_split
import random as rd
import matplotlib.pyplot as plt
from sklearn.svm import SVC
class SvmModel(object):
def __init__(self, C, kernel, kernel_params, max_iter, tol, eps):
self.C = C
self.kernel = kernel
self.kernel_params = kernel_params
self.max_iter = max_iter
self.tol = tol
self.eps = eps
def linear_kernel(self, x1, x2):
'''线性核函数'''
res = x1.dot(x2.T)
return res
def poly_kernel(self, x1, x2):
'''多项式核函数'''
zeta = self.kernel_params.get("zeta", 1.0)
gamma = self.kernel_params.get("gamma", 1.0)
degree = self.kernel_params.get("degree", 3.0)
res = (zeta + gamma*x1.dot(x2.T))**degree
return res
def rbf_kernel(self, x1, x2):
'''高斯核函数'''
gamma = self.kernel_params.get("gamma", 1.0)
x1 = np.atleast_2d(x1)
x2 = np.atleast_2d(x2)
res = np.exp(-gamma * dist.cdist(x1, x2)**2)
return res
def random_idx(self, i, N):
'''a2索引的选择:随机搜索'''
j = i
while j == i:
j = np.random.randint(0, N)
return j
def choose_alpha(self, y_train, N, a, b, K):
'''搜索合适的a1和a2'''
# 外循环:搜索违反KKT条件的样本点,优先选择支持向量点
unbounded = [i for i in range(N) if a[i] == 0]
bounded = [i for i in range(N) if i not in unbounded]
# 合并外循环索引,令支持向量排在前
idx_list = []
idx_list.extend(bounded)
idx_list.extend(unbounded)
for i in idx_list:
gi = (a * y_train).dot(K[:, i]) + b
# Ei = gi - y_train[i]
# 内循环:针对违反KKT条件的a1,找到对应的a2
if (a[i] < self.C and y_train[i]*gi < 1 - self.tol) or \
(a[i] > 0 and y_train[i]*gi > 1 + self.tol):
# j = np.argmax(np.abs(Ei - E))
j = self.random_idx(i, N)
else:
# 满足KKT条件的点则跳过
continue
return i, j
def find_bounds(self, y_train, i, j, ai_old, aj_old):
'''确定上下确界'''
if y_train[i] == y_train[j]:
L = max(0.0, ai_old + aj_old - self.C)
H = min(self.C, ai_old + aj_old)
else:
L = max(0.0, aj_old - ai_old)
H = min(self.C, self.C + aj_old - ai_old)
return L, H
def clip_a(self, a_unc, L, H):
'''a边界截断'''
if a_unc > H:
a_new = H
elif a_unc < L:
a_new = L
else:
a_new = a_unc
return a_new
def clip_b(self, bi_new, bj_new, ai_new, aj_new):
'''b边界截断'''
if 0 < ai_new < self.C:
b = bi_new
elif 0 < aj_new < self.C:
b = bj_new
else:
b = (bi_new + bj_new) / 2.0
return b
def fit(self, x_train, y_train):
'''模型训练'''
# 核函数映射
if self.kernel == "linear":
K = self.linear_kernel(x_train, x_train)
elif self.kernel == "poly":
K = self.poly_kernel(x_train, x_train)
elif self.kernel == "rbf":
K = self.rbf_kernel(x_train, x_train)
else:
raise ValueError("kernel must be 'linear', 'poly' or 'rbf'")
# 参数初始化
N = len(x_train)
a = np.zeros([N])
b = 0
g = (a * y_train).dot(K) + b
E = g - y_train
# 参数结果保存列表
a_res = []
b_res = []
E_res = []
# 迭代
for step in range(self.max_iter):
# 搜索合适的 a1 和 a2
i, j = self.choose_alpha(y_train, N, a, b, K)
# 计算对应的 E1
gi = (a * y_train).dot(K[:, i]) + b
Ei = gi - y_train[i]
# 计算对应的 E2
gj = (a * y_train).dot(K[:, j]) + b
Ej = gj - y_train[j]
# 计算 eta
eta = K[i, i] + K[j, j] - 2.0 * K[i, j]
# 保存 a1 和 a2 的旧值
ai_old, aj_old = a[i], a[j]
# 计算 a2 的未剪辑值
aj_unc = aj_old + y_train[j] * (Ei - Ej) / (eta + self.eps)
# 计算 a2 的下确界和上确界
L, H = self.find_bounds(y_train, i, j, ai_old, aj_old)
# 计算 a2 的新值
aj_new = self.clip_a(aj_unc, L, H)
# 计算 a1 的新值
ai_new = ai_old + y_train[i] * y_train[j] * (aj_old - aj_new)
a[i], a[j] = ai_new, aj_new
# 计算 b
bi_new = b - Ei - y_train[i] * K[i,i] * (ai_new-ai_old) - \
y_train[j] * K[i,j] * (aj_new-aj_old)
bj_new = b - Ej - y_train[i] * K[i,j] * (ai_new-ai_old) - \
y_train[j] * K[j,j] * (aj_new-aj_old)
b = self.clip_b(bi_new, bj_new, ai_new, aj_new)
# 更新 E 列表
g = (a * y_train).dot(K) + b
E = g - y_train
# 保存参数
E_res.append(np.sum(np.abs(E)))
a_res.append(a)
b_res.append(b)
return E_res, a_res, b_res
def predict(self, a, b, x_train, x_predict):
'''模型预测'''
# 适配核函数
if self.kernel == "linear":
K = self.linear_kernel(x_train, x_predict)
elif self.kernel == "poly":
K = self.poly_kernel(x_train, x_predict)
elif self.kernel == "rbf":
K = self.rbf_kernel(x_train, x_predict)
else:
raise ValueError("kernel must be 'linear', 'poly' or 'rbf'")
# 预测
y_pred = np.sign((a * y_train).dot(K) + b)
return y_pred
def get_score(self, y_true, y_pred):
'''模型评估'''
score = sum(y_true == y_pred) / len(y_true)
return score
if __name__ == "__main__":
# 构造二分类数据集
N = 50
x1 = np.random.uniform(low=1, high=5, size=[N,2]) + np.random.randn(N, 2)*0.01
y1 = np.tile(-1.0, N)
x2 = np.random.uniform(low=6, high=10, size=[N,2]) + np.random.randn(N, 2)*0.01
y2 = np.tile(1.0, N)
x = np.concatenate([x1,x2], axis=0)
y = np.concatenate([y1,y2])
x, y = shuffle(x, y, random_state=0)
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)
# linear
model = SvmModel(C=1.0, kernel="linear", kernel_params=None, max_iter=1000, tol=10**-4, eps=10**-6)
E_res, a_res, b_res = model.fit(x_train, y_train)
# poly
# model = SvmModel(C=1.0, kernel="poly", kernel_params={"zeta":1.0, "gamma":0.01, "degree":3.0},
# max_iter=1000, tol=10**-4, eps=10**-6)
# E_res, a_res, b_res = model.fit(x_train, y_train)
# rbf
# model = SvmModel(C=1.0, kernel="rbf", kernel_params={"gamma":10},
# max_iter=1000, tol=10**-4, eps=10**-6)
# E_res, a_res, b_res = model.fit(x_train, y_train)
# 对偶问题最优解
a_best = a_res[np.argmin(E_res)]
print(f"对偶问题最优解为:{a_best[a_best != 0]}")
# 原问题最优解
b_best = b_res[np.argmin(E_res)]
w_best = (a_best * y_train).dot(x_train)
print(f"原问题最优解为:{w_best, b_best}")
# 支持向量
x_support = x_train[a_best != 0]
# predict on testSet
y_pred = model.predict(a_best, b_best, x_train, x_test)
score = model.get_score(y_test, y_pred)
print(f"SvmModel 预测准确率:{score}")
# 运行sklearn算法
clf = SVC(C=1.0, kernel="linear", max_iter=1000)
clf.fit(x_train, y_train)
# 对偶问题最优解
alpha = clf.dual_coef_
print(f"sklearn对偶问题最优解为:{alpha}")
# 原问题最优解
w = clf.coef_[0]
b = clf.intercept_
print(f"sklearn原问题最优解为:{w, b}")
# 支持向量
x_support = x_train[clf.support_]
y_pred = clf.predict(x_test)
score = sum(y_test == y_pred) / len(y_test)
print(f"sklearn 预测准确率:{score}")
运行结果:
对偶问题最优解为:[0.07311687 0.07311687]
原问题最优解为:(array([0.24793193, 0.29114169]), -3.064410196685151)
SvmModel 预测准确率:1.0
sklearn对偶问题最优解为:[[-0.16756058 0.16756058]]
sklearn原问题最优解为:(array([0.4837058 , 0.31804058]), array([-4.32046255]))
sklearn 预测准确率:1.0
可见,该例存在两个支持向量,但 Sklearn 库的求解结果和自写算法存在一些区别,令人不解的是 Sklearn 库中得到的对偶问题最优解出现了负值。
返回主页