python实现DSA签名数字证书
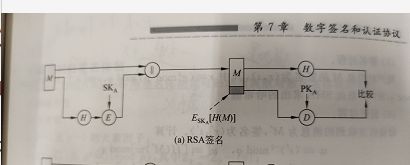
一、数字签名
采用数字签名,能完成这些功能:
(1)确认信息是由签名者发送的;
(2)确认信息自签名后到收到为止,未被修改过;
(3)签名者无法否认信息是由自己发送的。
与公钥加密不同,数字签名是用私钥加密,公钥解密,那么每个人都能识别他的身份
二、DSA签名
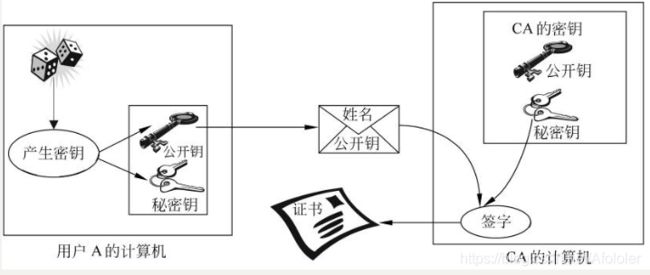
1、随机选取p、q、g、h,1 g ≡ \equiv ≡ h p − 1 q h^\frac{p-1}{q} hqp−1mod p 并且 h p − 1 q h^\frac{p-1}{q} hqp−1>1 (g是p的原根) 2、 选择密钥x(用户的密钥) 0 3、 选择密钥k(本次签名的密钥) 4、 计算用户对消息的签名 (r,s) r ≡ \equiv ≡ g k g^k gkmodpmodq (用户的身份证明) 可以在消息签名前大量生成 s ≡ \equiv ≡ k − 1 k^-1 k−1 * (H(M)+xr)modq 其中 k^-1用扩展欧几里得算法计算,H(M)采用SHA哈希算法 接收方还有公钥y,y ≡ \equiv ≡ g x g^x gxmodp 可能有人问了,既然这个等式中都出现k了,为什么说恢复k是不可行的呢 这里只出现了 g k g^k gk,而通过这种方式求出k是不可行的 数字签名就是CA管理机构对某A身份的认证,CA机构一般是国际机构或者知名机构,CA签名的有效性乃至于电脑的操作系统、浏览器都要提前预装有关资料的 比如用户A把公钥、自己的身份、时间等信息写在一张纸上,权威机构通过数字签名在纸上盖章,形成了有公信力的证书,访问者(浏览器)查询这张证书,就能确定A的身份了,因为访问者发信息,只有A拥有得私钥才能解密并正确回馈 HTTPS连接就利用了数字签名的特性,如果访问网站的时候提示不安全,那就要小心了 建议:选取较大的p和q
三、验证过程
import random
import hashlib
def rabin_miller(num):
s = num - 1
t = 0
while s % 2 == 0:
s = s // 2
t += 1
for trials in range(5):
a = random.randrange(2, num - 1)
v = pow(a, s, num)
if v != 1:
i = 0
while v != (num - 1):
if i == t - 1:
return False
else:
i = i + 1
v = (v ** 2) % num
return True
def is_prime(num):
# 排除0,1和负数
if num < 2:
return False
# 创建小素数的列表,可以大幅加快速度
# 如果是小素数,那么直接返回true
small_primes = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997]
if num in small_primes:
return True
# 如果大数是这些小素数的倍数,那么就是合数,返回false
for prime in small_primes:
if num % prime == 0:
return False
# 如果这样没有分辨出来,就一定是大整数,那么就调用rabin算法
return rabin_miller(num)
# 得到大整数,默认位数为1024
def get_prime(key_size):
while True:
num = random.randrange(2**(key_size-1), 2**key_size)
if is_prime(num):
return num
def get_p(q):
while True:
t = random.randint(2**300,2**370)
p = t *q+1
if is_prime(p):
return p
def get_g(p,q):
while True:
h = random.randrange(2, q - 2)
g = pow(h, (p - 1) // q, p)
# print(p,q)
# print((p - 1) / q)
# print(g)
if g > 1:
return g
def EX_GCD(a,b,arr): #扩展欧几里得
if b == 0:
arr[0] = 1
arr[1] = 0
return a
g = EX_GCD(b, a % b, arr)
t = arr[0]
arr[0] = arr[1] #x before = y
arr[1] = t - int(a / b) * arr[1]
return g
def ModReverse(a,n): #ax=1(mod n) 求a模n的乘法逆x
arr = [0,1,]
gcd = EX_GCD(a,n,arr)
if gcd == 1:
return (arr[0] % n + n) % n
else:
return -1
if __name__ == '__main__':
q= get_prime(150)
p = get_p(q)
g = get_g(p,q)
x = 5
# 用户的公开要
y = pow(g, x, p)
# 代签消息的秘密数
k = random.randint(1,q-1)
h = int(hashlib.sha1("hello".encode('utf-8')).hexdigest(),16)
# 对信息M的签名
print("p:"+str(p))
print("q:"+str(q))
print("g:"+str(g))
print("y:"+str(y))
r = pow(g,k,p)%q
k_1 = ModReverse(k, q)
s = k_1 *(h + x * r) % q
# 验证过程
print("签名(r,s)为:"+str(r),str(s)) #签名结果
s_1 = ModReverse(s, q)
w = s_1 % q
u1 = h* w % q
u2 = (r * w )% q
v = (pow(g, u1, p) * pow(y, u2, p))%p % q
if v == r:
print("签名有效")
else:
print("签名无效")
四、数字签名的应用
五、可能发生的错误