程序 = 数据结构 + 算法
数据
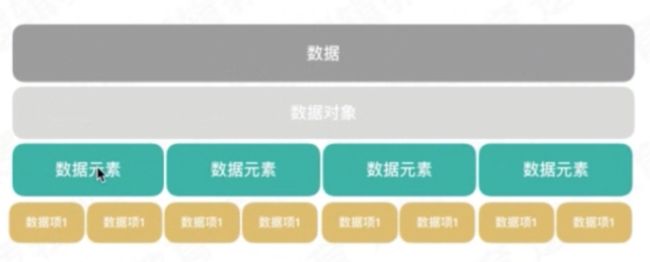
数据: 程序的操作对象,用于描述客观事物.
数据的特点: 1️⃣ 可以输入到计算机 2️⃣ 可以被计算机处理
数据项: 一个数据元素由若干数据项组成
数据元素: 组成数据的对象的基本单位
数据对象: 性质相同的数据元素的集合(类似于数组)
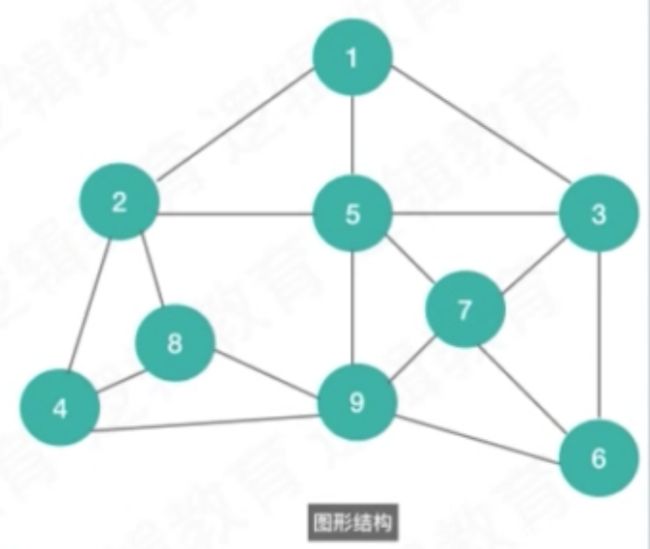
结构: 数据元素之间不是独立的,存在特定的关系.这些关系即是结构;
数据结构:指的数据对象中的数据元素之间的关系
#include
//声明一个结构体类型
struct Teacher{ //一种数据结构
char *name; //数据项--名字
char *title; //数据项--职称
int age; //数据项--年龄
};
int main(int argc, const char * argv[]) {
struct Teacher t1; //数据元素;
struct Teacher tArray[10]; //数据对象;
t1.age = 18; //数据项
t1.name = "CC"; //数据项
t1.title = "讲师"; //数据项
printf("老师姓名:%s\n",t1.name);
printf("老师年龄:%d\n",t1.age);
printf("老师职称:%s\n",t1.title);
return 0;
}
数据结构
数据与数据直接的逻辑关系
-
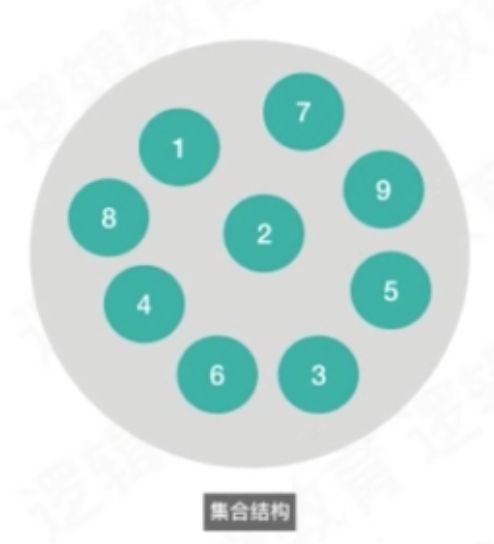
[Set]
-
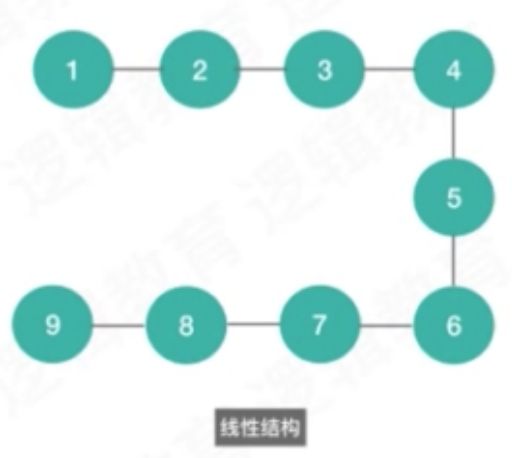
[Array, String, Dictionary]
-
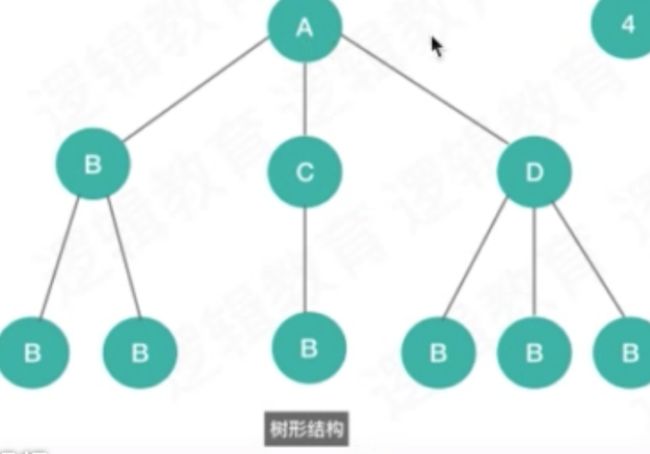
[二叉树] 1对多
-
多对多
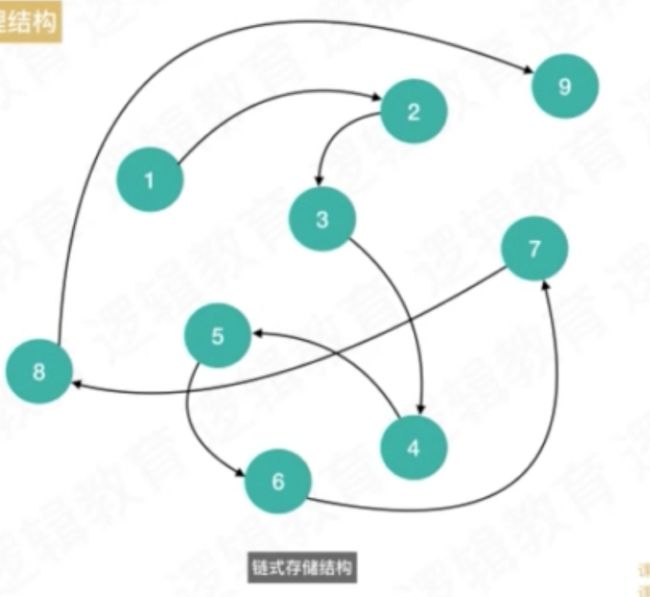
- 物理结构
-
数组
-
链表
算法比较
算法:算法是解决特定问题步骤的描述, 在计算机中表现为指令的有限序列,并且每一个指令表示一个或者多个操作。
算法的特性
- 输入输出
- 有穷性
- 确定性
- 可行性
算法要求
- 正确性
- 可读性
- 健壮性
- 时间效率和存储量低
时间复杂度
大O表示法
- 用常数1取代运行时间中所有常数 3->1 O(1)
- 在修改运行次数函数中,只保留最高阶项 n3+2n2+5 -> O(n^3)
- 如果在最高阶存在且不等于1,则去除这个项目相乘的常数 2n^3 -> n^3
/*
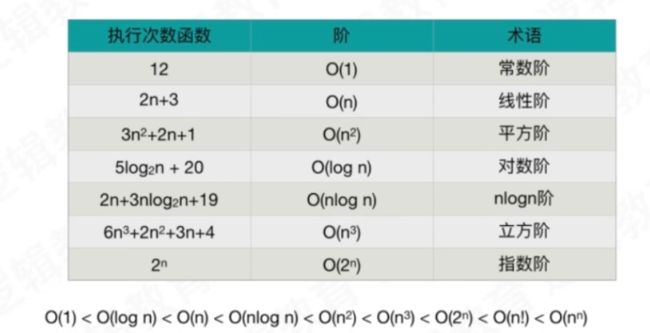
时间复杂度术语:
1. 常数阶
2. 线性阶
3. 平方阶
4. 对数阶
5. 立方阶
6. nlog阶
7. 指数阶(不考虑) O(2^n)或者O(n!) 除非是非常小的n,否则会造成噩梦般的时间消耗. 这是一种不切实际的算法时间复杂度. 一般不考虑!
*/
/* 1. 常数阶时间复杂度计算 O(1) */
//1+1+1 = 3 O(1)
void testSum1(int n){
int sum = 0; //执行1次
sum = (1+n)*n/2; //执行1次
printf("testSum1:%d\n",sum);//执行1次
}
//1+1+1+1+1+1+1 = 7 O(1)
void testSum2(int n){
int sum = 0; //执行1次
sum = (1+n)*n/2; //执行1次
sum = (1+n)*n/2; //执行1次
sum = (1+n)*n/2; //执行1次
sum = (1+n)*n/2; //执行1次
sum = (1+n)*n/2; //执行1次
printf("testSum2:%d\n",sum);//执行1次
}
//x=x+1; 执行1次 O(1)
void add(int x){
x = x+1;
}
/*2.线性阶时间复杂度*/
//x=x+1; 执行n次 O(n)
void add2(int x,int n){
for (int i = 0; i < n; i++) {
x = x+1;
}
}
//1+(n+1)+n+1 = 3+2n -> O(n)
void testSum3(int n){
int i,sum = 0; //执行1次
for (i = 1; i <= n; i++) { //执行n+1次
sum += i; //执行n次
}
printf("testSum3:%d\n",sum); //执行1次
}
/*3.对数阶*/
/*2的x次方等于n x = log2n ->O(logn)*/
void testA(int n){
int count = 1; //执行1次
//n = 10
while (count < n) {
count = count * 2;
}
}
/*4.平方阶*/
//x=x+1; 执行n*n次 ->O(n^2)
void add3(int x,int n){
for (int i = 0; i< n; i++) {
for (int j = 0; j < n ; j++) {
x=x+1;
}
}
}
//n+(n-1)+(n-2)+...+1 = n(n-1)/2 = n^2/2 + n/2 = O(n^2)
//sn = n(a1+an)/2
void testSum4(int n){
int sum = 0;
for(int i = 0; i < n;i++)
for (int j = i; j < n; j++) {
sum += j;
}
printf("textSum4:%d",sum);
}
//1+(n+1)+n(n+1)+n^2+n^2 = 2+3n^2+2n -> O(n^2)
void testSum5(int n){
int i,j,x=0,sum = 0; //执行1次
for (i = 1; i <= n; i++) { //执行n+1次
for (j = 1; j <= n; j++) { //执行n(n+1)
x++; //执行n*n次
sum = sum + x; //执行n*n次
}
}
printf("testSum5:%d\n",sum);
}
/*5.立方阶*/
void testB(int n){
int sum = 1; //执行1次
for (int i = 0; i < n; i++) { //执行n次
for (int j = 0 ; j < n; j++) { //执行n*n次
for (int k = 0; k < n; k++) {//执行n*n*n次
sum = sum * 2; //执行n*n*n次 O(n^3)
}
}
}
}
int main(int argc, const char * argv[]) {
testSum1(100);
testSum2(100);
testSum3(100);
return 0;
}
- 按最高阶算
空间复杂度
/*
程序空间计算因素:
1. 寄存本身的指令
2. 常数
3. 变量
4. 输入
5. 对数据进行操作的辅助空间
在考量算法的空间复杂度,主要考虑算法执行时所需要的辅助空间.
空间复杂度计算:
问题: 数组逆序,将一维数组a中的n个数逆序存放在原数组中.
*/
#include
int main(int argc, const char * argv[]) {
// insert code here...
printf("Hello, World!\n");
int n = 5;
int a[10] = {1,2,3,4,5,6,7,8,9,10};
//算法实现(1)
int temp;
for(int i = 0; i < n/2 ; i++){
temp = a[i];
a[i] = a[n-i-1];
a[n-i-1] = temp;
}
for(int i = 0;i < 10;i++)
{
printf("%d\n",a[i]);
}
//算法实现(2)
int b[10] = {0};
for(int i = 0; i < n;i++){
b[i] = a[n-i-1];
}
for(int i = 0; i < n; i++){
a[i] = b[i];
}
for(int i = 0;i < 10;i++)
{
printf("%d\n",a[i]);
}
return 0;
}