一、准备
噪声是在拟合过程中常用的干扰手段,常用的噪声:
1.统一分布 U(a,b)
f ( x ) = { 1 i f a ≤ x < b 0 o t h e r f(x)=\begin{cases}\begin{aligned}1&\quad if\quad a\le x
import numpy as np
x=np.random.uniform(a,b,100) #产生长度为100的U(a,b)
2.正态分布N( μ \mu μ, σ 2 \sigma^2 σ2)
import numpy as np x=np.random.normal(mu, sig, 100) #产生长度为100的N(mu, sqart(sig))
二、三次样条插值
def spline_fit():
size = 20
x = np.linspace(-10, 10, size)
y = np.sin(x) + np.random.normal(0, 0.1, size)
y2 = [0] * len(y)
# for y_i in y:
pp.plot(x, y)
cs = CubicSpline(x, y)
x2 = x = np.linspace(-10, 10, size * 100)
pp.plot(x2, cs(x2))
pp.show()
三、最小二乘拟合
def least_square():
f = lambda p0, xx: p0[0] * np.sin(xx * p0[1]) + p0[2]
LEN = 100
x = np.linspace(-1, 1, LEN)
y = x ** 2 + 5
# 默认情况,param只会返回求得的参数和返回的错误码,1-4为成功,5-8为失败,如果想输出更多参数,可以指定full_out=1,可以看到出错原因和其他参数
param = leastsq(lambda p0, xx, yy: f(p0, xx) - yy, (1, 1, 1), args=(x, y)) #初值的选择比较重要,如果选取不当,容易陷入局部最优
print(param)
pp.scatter(x, y)
p0 = param[0]
pp.plot(x, f(p0, x))
pp.show()
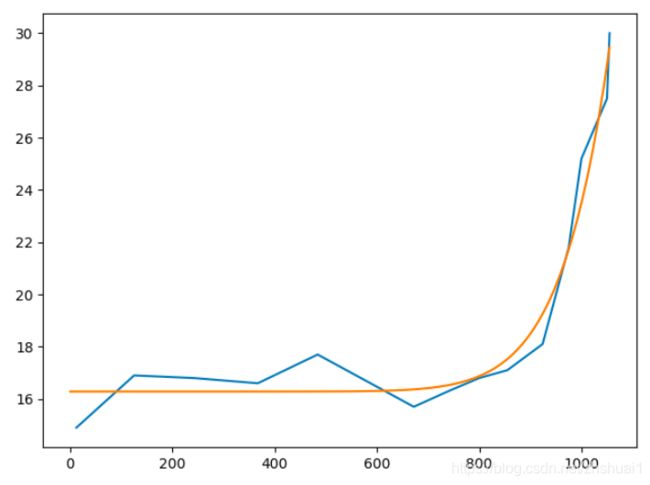
最小二乘的初值选取非常重要,以下是三份完全相同的数据,虽然最后都收敛了,但是初值不同,得到了完全不同的拟合结果
初值为 ( 1 , 2 , 1 ) (1,2,1) (1,2,1)
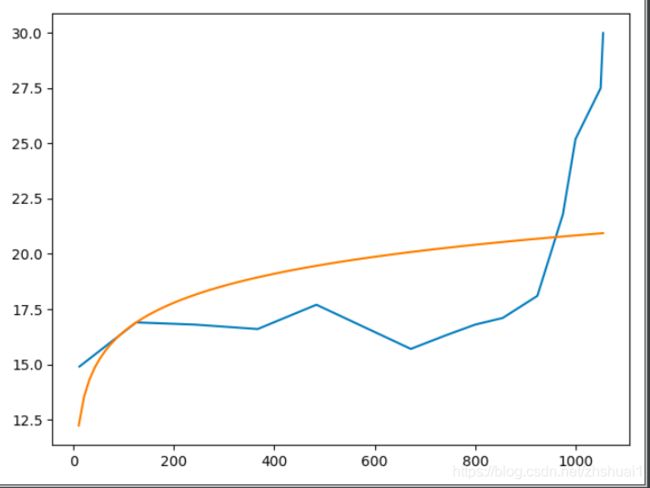
初值为 ( 1 , 1 , 1 ) (1,1,1) (1,1,1)
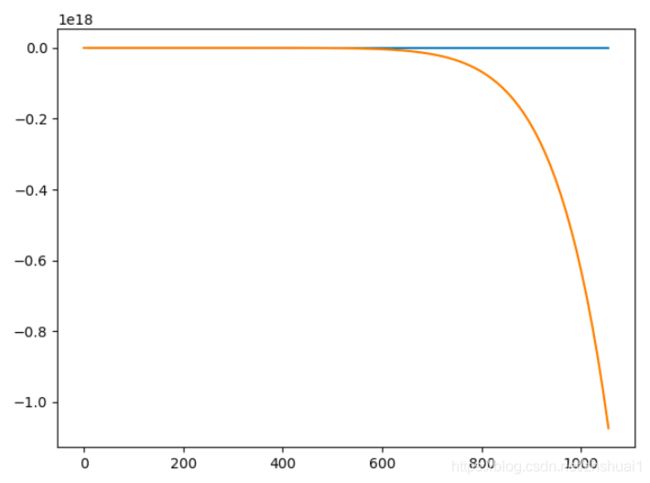
初值为 ( 10 , 10 , 1 ) (10,10,1) (10,10,1)
四、拉格朗日乘子法
def lagrange()
from scipy.optimize import minimize
import numpy as np
e = 1e-10
fun = lambda x: 8 * (x[0] * x[1] * x[2]) # f(x,y,z) =8 *x*y*z
cons = ({'type': 'eq', 'fun': lambda x: x[0] ** 2 + x[1] ** 2 + x[2] ** 2 - 1}, # x^2 + y^2 + z^2=1
{'type': 'ineq', 'fun': lambda x: x[0] - e}, # x>=e等价于 x > 0
{'type': 'ineq', 'fun': lambda x: x[1] - e},
{'type': 'ineq', 'fun': lambda x: x[2] - e}
)
x0 = np.array((1.0, 1.0, 1.0)) # 设置初始值
res = minimize(fun, x0, method='SLSQP', constraints=cons)
print('最大值:', res.fun)
print('最优解:', res.x)
print('迭代终止是否成功:', res.success)
print('迭代终止原因:', res.message)
到此这篇关于教你如何利用python进行数值分析的文章就介绍到这了,更多相关python数值分析内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!