梯度下降法(Gradient Descent)优化函数的详解（1）梯度下降法（Gradient Descent）
- 前言
- 梯度下降法(Gradient Descent)优化函数的详解（0）线性回归问题
- 梯度下降法(Gradient Descent)优化函数的详解（1）批量梯度下降法（Batch Gradient Descent）
- 梯度下降法(Gradient Descent)优化函数的详解（2）随机梯度下降法（SGD Stochastic Gradient Descent）
- 梯度下降法(Gradient Descent)优化函数的详解（3）小批量随机梯度下降法（mini-batch SGD ）
- 几种算法的比较
梯度下降法（Gradient Descent）
梯度下降（GD）是将风险函数、损失函数最小化的一种常用的方法，是神经网络模型训练最常用的优化算法。对于深度学习模型，基本都是采用梯度下降算法来进行优化训练的。
基本原理
目标函数J(θ)关于参数θ的梯度是目标函数上升最快的方向。对于最小化优化问题，只需要将参数沿着梯度相反的方向前进一个步长，就可以实现目标函数的下降。这个步长又称为学习速率η。参数更新公式如下：
θ ← θ − η ▽ θ J ( θ ) \theta \leftarrow \theta -\eta \bigtriangledown _{\theta }J(\theta ) θ←θ−η▽θJ(θ)
算法详解
上一篇讲到最基本的线性回归问题，假设只有一个变量。那么会得到直线y = ax + b，最终就是优化参数a、b，寻找最小的loss。
l o s s = J ( θ ) = 1 2 m ∑ i = 1 m ( y θ ( x i ) − y i ) 2 loss = J(\theta ) = \frac{1}{2m}\sum_{i=1}^{m}(y_{ \theta }(x_{i})- y_{i})^{2} loss=J(θ)=2m1i=1∑m(yθ(xi)−yi)2
显然loss函数是一个二次函数，问题就转化成了如何求二次函数的最小值。
举例说明
step1：假设我们要优化的函数是 y = x 2 y = x^2 y=x2，初始条件为 x 0 x_0 x0 = 2， y 0 y_0 y0 = 4。图示如下
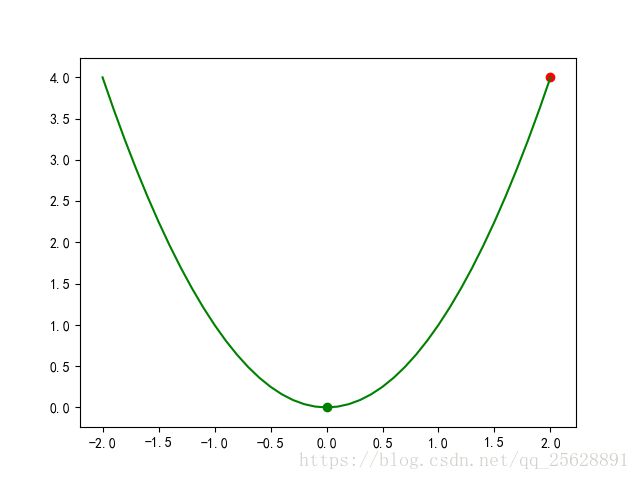
图中红色的点就是我们的初始点，很显然，我们想要找的最终最优点是绿色的点(0,0) 。
step2：对目标函数求微分
d y d x = 2 x \frac{dy}{dx} =2x dxdy=2x
这就是所谓的梯度，当x=2的时候，可以求得该点的梯度为4，简单来说就是当前这一点的’倾斜程度’是4。
step3：下面给出几个例子
| x | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| y | 4 | 1 | 0 | 1 | 4 |
| 梯度 | -4 | -2 | 0 | 2 | 4 |
从表格中很容易发现，梯度的绝对值越大，数据点所在的地方就越陡。数字为正数时，越大，表示越向右上方陡峭，反之亦然。好了，懂了什么是梯度，下面我们就来聊聊梯度下降是什么。
step4：现在我们先假设我们自己就是一个球，呆在图中的红点处，我们的目标是到绿点处，该怎么走呢？
很简单，顺着坡向下走就行了。现在球在(2,4)点处，这一点的倾斜程度是4，向右上方陡峭，接下来要做的就是向山下走。
step5：那么每一次走多远呢？
先小心一点，按当前倾斜程度的1%向下走。也就是 x n e w x_{new} xnew = x 0 x_0 x0 - 0.01*4， x n e w x_{new} xnew = 1.96， y n e w y_{new} ynew = 3.8416<4。小球成功的往下滚了一点，这样一直滚下去，最终就会滚到绿色的点，如下图
红色的曲线表示了小球的滚动路线。
数学公式
梯度下降法转换成数学语言就是在每一次迭代按照一定的学习率α沿梯度的反方向更新参数，直至收敛，公式
θ t + 1 = θ t − α d f d θ \theta _{t+1} = \theta _{t}-\alpha \frac{df}{d\theta } θt+1=θt−αdθdf
接下来我们回到房价预测问题上。
step1：
y p , i = a x i + b l o s s = 1 2 m ∑ i = 1 m ( y p , i − y i ) 2 y_{p,i} = ax_i + b \qquad \qquad loss = \frac{1}{2m}\sum_{i=1}^{m}(y_{p,i}-y_i)^2 yp,i=axi+bloss=2m1i=1∑m(yp,i−yi)2
step2：将上面两个方程合并，并把1/2放到方程右边
l o s s = 1 m ∑ i = 1 m 1 2 ( a x i + b − y i ) 2 loss = \frac{1}{m}\sum_{i=1}^{m}\frac{1}{2}(ax_i + b-y_i)^2 loss=m1i=1∑m21(axi+b−yi)2
一共有m项累加，我们单拿出来一项来分析。
l o s s i = 1 2 ( a x i + b − y i ) 2 loss_i = \frac{1}{2}(ax_i + b-y_i)^2 lossi=21(axi+b−yi)2
step3：要优化的参数有两个，分别是a和b，我们分别对他们求微分，也就是偏微分
∂ l o s s i ∂ a = ( a x i + b − y i ) x i ∂ l o s s i ∂ b = a x i + b − y i \frac{\partial loss_i}{\partial a} = (ax_i+b-y_i)x_i \qquad \qquad \frac{\partial loss_i}{\partial b} = ax_i+b-y_i ∂a∂lossi=(axi+b−yi)xi∂b∂lossi=axi+b−yi
这里我们看到了loss函数为什么要在前面加一个1/2，目的就是在求偏微分的时候，可以把平方项中和掉，方便后面的计算。
step4：自然地我们将每一个 ∂ l o s s i ∂ a \frac{\partial loss_i}{\partial a} ∂a∂lossi和 ∂ l o s s i ∂ b \frac{\partial loss_i}{\partial b} ∂b∂lossi累加起来得到
∂ l o s s i ∂ a = 1 m ∑ i = 1 m ∂ l o s s i ∂ a ∂ l o s s i ∂ b = 1 m ∑ i = 1 m ∂ l o s s i ∂ b \frac{\partial loss_i}{\partial a} =\frac{1}{m}\sum_{i=1}^{m} \frac{\partial loss_i}{\partial a} \qquad \qquad \frac{\partial loss_i}{\partial b} = \frac{1}{m}\sum_{i=1}^{m}\frac{\partial loss_i}{\partial b} ∂a∂lossi=m1i=1∑m∂a∂lossi∂b∂lossi=m1i=1∑m∂b∂lossi
step5： ∂ l o s s i ∂ a \frac{\partial loss_i}{\partial a} ∂a∂lossi记为 ▽ a \bigtriangledown a ▽a， ∂ l o s s i ∂ b \frac{\partial loss_i}{\partial b} ∂b∂lossi记为 ▽ b \bigtriangledown b ▽b，分别表示loss在a、b方向的梯度，更新参数的方式如下
a n e w = a − α ▽ a b n e w = b − α ▽ b a_{new} = a - \alpha ▽a \qquad \qquad b_{new} = b - \alpha ▽ b anew=a−α▽abnew=b−α▽b
算法实现
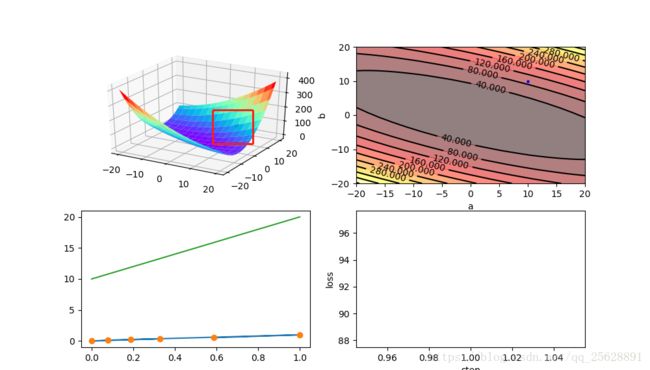
写了这么多公式，是时候直观的看一看梯度下降法是怎么一回事了。下面将绘制四幅图，分别是
- 在a,b的一定的取值范围内，计算所有的loss，绘制出分布图
- 将这张分布图拍扁，画出等高线图
- 绘制原始的数据折线以及依据a,b绘制预测直线
- 绘制在训练过程中loss的变化
如下
我们看到图1和之前二次函数的那个例子很像，只不过是在三维空间内的一个曲面，初始的参数选择a=10,b=10 ，可以看到图1上曲面右侧有一个浅浅的点，就是初始值了。图二是等高线图，俯视更加明显，等高线图主要是为了之后训练的过程中可视化更清晰。图三上方的绿线是根据选择的初始值绘制的，下方是真实的实验数据，可以看出差距很远，需要优化的步骤还很多。将学习率α设置为0.01, 经过200次迭代，结果如下图
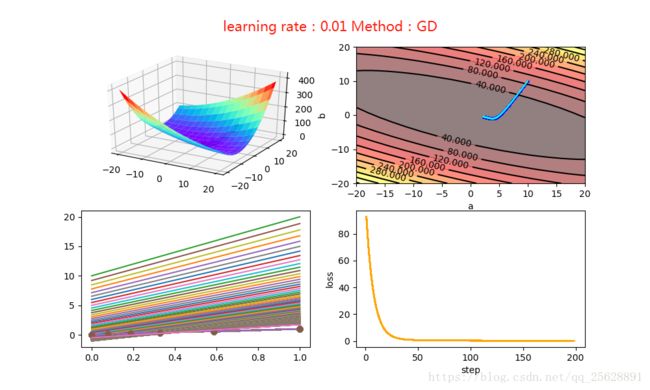
图一和图二都可以很直观的看到loss的减小。图三也从模型上给出了最终逼近的过程。图四可以看出下降还是很快的。
值得注意的是，不同的学习率对算法的收敛速度影响很大,下图是α=0.2的结果
基本在前10次迭代就快速收敛。
但是如果学习率设置的太大的话，很容易造成发散。说白了就是步子迈的太大了，一步迈到对面更高的山坡上去了，结果越迈越高，最后就不知道跑到哪里去了，如下图(α=0.3)
所以梯度下降算法中选取适当的学习速率很重要：学习速率过小时，虽然可以收敛，但是收敛速度慢，而过大时导致训练震荡，而且可能会发散。如图所示
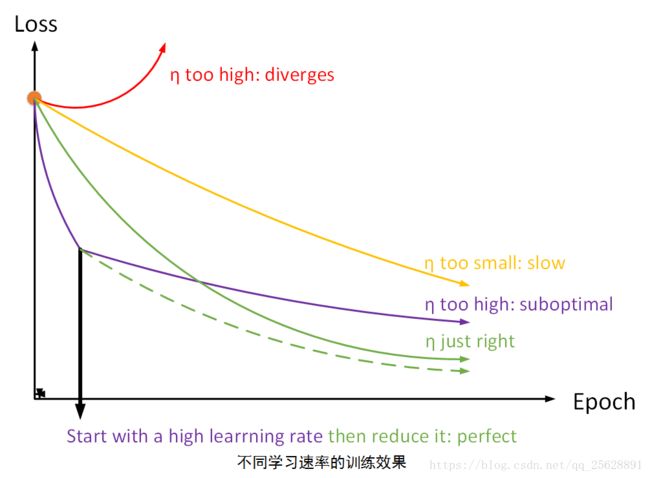
理想的学习速率是：
- 刚开始设置较大，有很快的收敛速度，然后慢慢衰减，保证稳定到达最优点。
梯度下降伪代码
输入参数：rate， x → \overrightarrow{x} x， y → \overrightarrow{y} y，scope
============> rate为设定的学习率
============> x → \overrightarrow{x} x为给定的模拟数据
============> x取值范围
============> scope 步长范围
输出参数：a，b，loss
1）：初始化a，b
2）：for i in len(x)
A：更新x的值： x[i] = (x[i] - x_min)/(x_max - x_min)
B：更新y的值： y[i] = (y[i] - y_min)/(y_max - y_min)
3）：for step in scope
\qquad ：for i in len(x)
\qquad \qquad A：累加da：all_da = all_da+ da(i)
\qquad \qquad B：累加db：all_db = all_db+ db(i)
\qquad A：更新a旳值：a = a - rate × all_da
\qquad B：更新b旳值：b = b - rate × all_db
4）end
理想的梯度下降算法要满足两点：
2. 收敛速度要快；
3. 能全局收敛
为了这个理想，出现了很多经典梯度下降算法的变种，下面有时间将分别介绍它们。
- 01 冲量梯度下降算法(Momentum optimization)
- 02 NAG(Nesterov Accelerated Gradient)
- 03 AdaGrad
- 04 RMSprop
- 05 Adam(Adaptive moment estimation)
代码地址：https://github.com/admin110/s0/blob/master/gradientDescent.py
上一篇：梯度下降法(Gradient Descent)优化函数的详解（0）线性回归问题
下一篇：梯度下降法(Gradient Descent)优化函数的详解（2）随机梯度下降法（SGD Stochastic Gradient Descent）