Dijkstra算法,中文叫狄克斯特拉算法,在地图中寻找两个地点之间的最短或者最快路径非常有用。狄克斯特拉算法是一个贪婪算法,也就是在处理过程中每一步都选择最佳路径。
例子
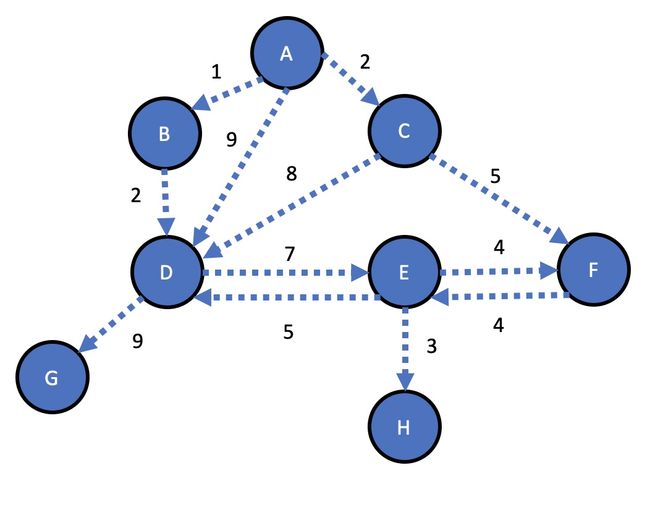
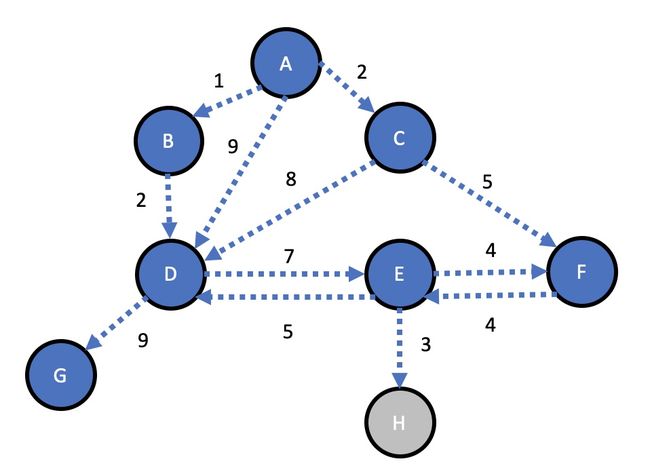
我们将通过一个有向图来演示一下狄克斯特拉算法的原理:
在狄克斯特拉算法中,我们首先要先选定一个起点,假设起点为 A。
- 第一条路径
从 A 出发,有三条路径,分别是:
- A 到 B,权重为 1
- A 到 D,权重为 9
- A 到 C,权重为 2
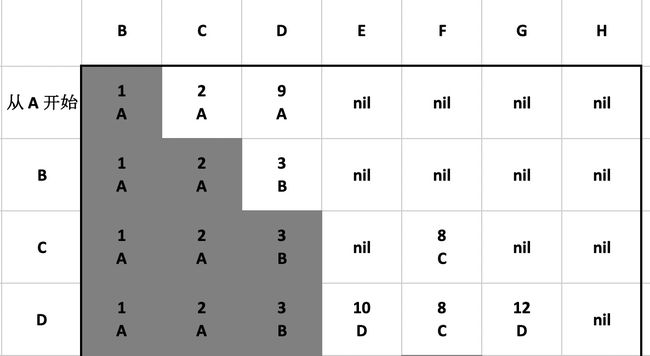
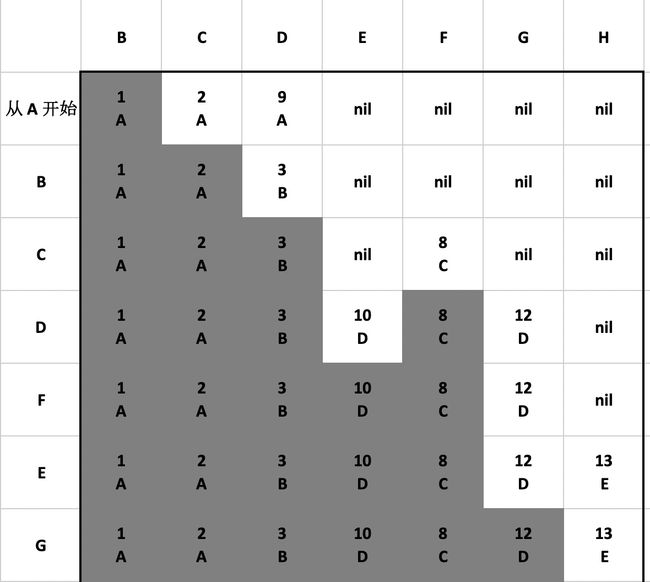
我们将用一个表来记录寻找路径的过程,目前标的状态如下:
表格中的后面的四个 nil 意思是暂时没有顶点通往 E、F、G 和 H。前三个单元格下面的 A 是指通往 B、C 和 D 的上一个顶点,上面的数字是指通往 B、C 和 D 的总权重。
- 第二条路径
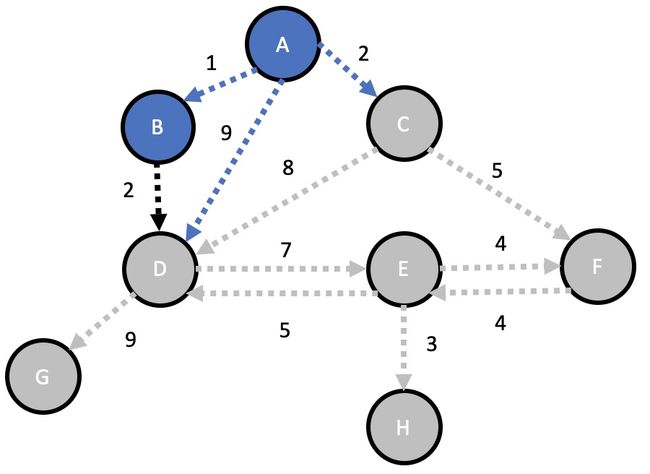
在狄克斯特拉算法中,每一步都要选择最优的路径。从第一步上看,权重最小的是从 A 到 B,所以我们就沿着 A 到 B 这条路走。B 只能通往 D,我们更新图和表格如下:
这一轮只有 B 通往 D,权重是 2,通往 D 的总权重是 4,因为从 A 到 B 到 D 为 1 + 2 = 3。在上一轮中,已经有一条路从 A 通往 D,权重为 9。在第二轮中我们找到了通往 D 的更近的路,所以我们在第二行中把通往 D 的上一个顶点更新为 3B。另外,因为从 A 通往 B 的权重是最小的,所以我们把它涂上背景色。
- 第三条路径
从上一步的表格看,下一个总权重最小的是 A 通往 C 的 2,所以沿着 C 走。有两条路:
- C 到 D 的总权重为 3 + 8 = 11
- C 到 F 的总权重为 3 + 5 = 8
C 到 D 的总权重比之前通往 D 的路大,所以不需要更新通往 D 的路。我们更新图和表格如下:
- 第四条路径
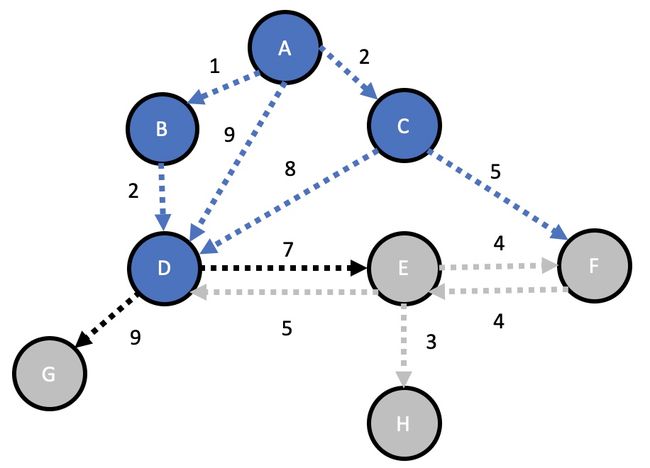
从上一步的表格看,下一个总权重最小的是 B 通往 D 的 3,所以沿着 D 走。有两条路:
- D 到 G 的总权重为 3 + 9 = 12
- D 到 E 的总权重为 3 + 7 = 10
更新图和表格如下:
- 第五条路径
从上一步的表格看,下一个总权重最小的是 C 通往 F 的 8,所以沿着 F 走。有一条路:
- F 到 E 的总权重为 8 + 4 = 12
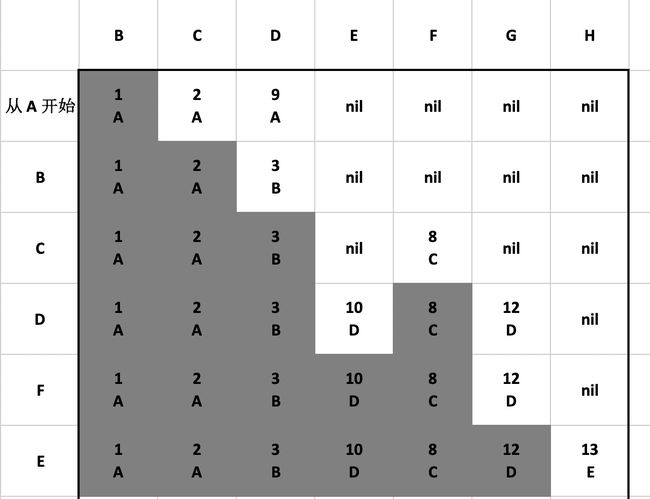
F 到 E 的总权重大于 D 到 E 的总权重,所以不需要更新通往 E 的路。更新图和表格如下:
- 第六条路径
从上一步的表格看,下一个总权重最小的是 D 通往 E 的 10,所以沿着 E 走。有三条路:
- E 到 F 的总权重为 10 + 4 = 14,已经有更近的路到 F,所以忽略这条路
- E 到 D 的总权重为 10 + 5 = 15,已经有更近的路到 D,所以忽略这条路
- E 到 H 的总权重为 10 + 3 = 13
更新图和表格如下:
- 第七条路径
从上一步的表格看,下一个总权重最小的是 D 通往 G 的 12,但是 G 没有其他邻居,也就意味着我能找到了到达 G 的最小路径,更新图和表格如下:
- 第八条路径
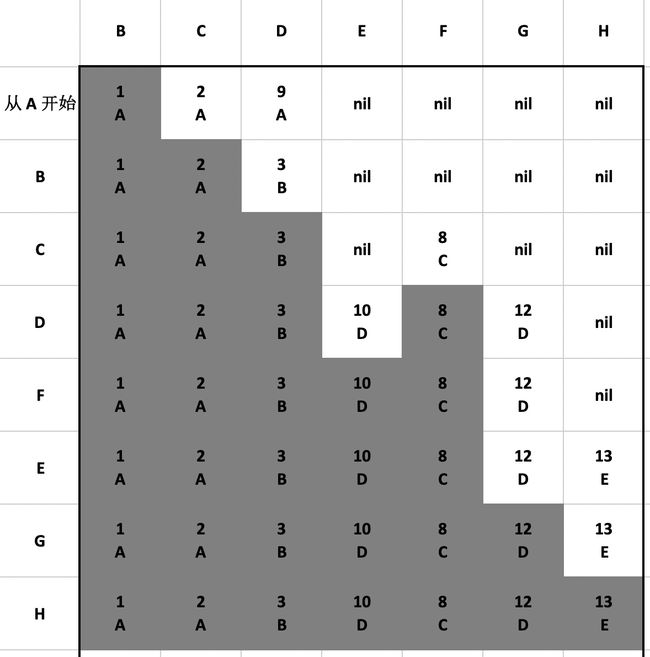
从上一步的表格看,下一个总权重最小的是 E 通往 H 的 12,但是 H 没有其他邻居,也就意味着我能找到了到达 H 的最小路径,更新图和表格如下:
所有的顶点都已经遍历,完成了狄克斯特拉算法。我们可以从图中直接得到通往 E 的最小权重为 10。然后反方向往回看就能得到通往 E 的最小路径,E --> D --> B --> A。示意图如下:
实现
在实现过程中,我们要用到优先队列,这里我们用最小优先队列,这样每次从队列中取出的元素都是目前总权重最小的顶点。
首先我们定义一个枚举,用来区分顶点的类型:
enum Visit {
case start // 顶点是起点
case edge(Edge) // 顶点关联着通往它的边
}
下面看下狄克斯特拉算法的具体实现:
class Dijkstra {
typealias Graph = AdjacencyList
let graph: Graph
init(graph: Graph) {
self.graph = graph
}
/// 找出从某个顶点开始的所有路径
func paths(from start: Vertex) -> [Vertex: Visit] {
// 用一个字典来记录每一步的数据,
// key 是顶点,value 是顶点类型或者是关联着通往这个顶点的边
var paths: [Vertex: Visit] = [start: .start]
// 创建最小优先队列,`order` 闭包队列中元素排序的条件,总权重最小的优先
var priorityQueue = PriorityQueue>(order: {
self.distance(to: $0, with: paths) <
self.distance(to: $1, with: paths)
})
priorityQueue.enqueue(start)
while let vertex = priorityQueue.dequeue() { // 取出队列当前最小权重的顶点
for edge in graph.edges(from: vertex) { // 遍历从这个顶点出发的边
guard let weight = edge.weight else {
continue
}
// 如果边的终点不在字典中,
// 或者从当前顶点出发达到边的终点总权重小于之前的路径,
// 更新路径,并把邻居加入到队列中
if paths[edge.destination] == nil ||
distance(to: vertex, with: paths) + weight <
distance(to: edge.destination, with: paths) {
paths[edge.destination] = .edge(edge)
priorityQueue.enqueue(edge.destination)
}
}
}
return paths
}
/// 根据记录着每一步数据的字典,找到到达某个终点的最小路径,
// 返回由边组成的有序数组
func shortestPath(to destination: Vertex,
with paths: [Vertex: Visit]) -> [Edge] {
var vertex = destination
var path: [Edge] = []
while let visit = paths[vertex], case .edge(let edge) = visit {
path = [edge] + path
vertex = edge.source
}
return path
}
// MARK: - Private
// 根据记录着每一步数据的字典中的数据,计算到达某一个终点的总权重
private func distance(to destination: Vertex,
with paths: [Vertex: Visit]) -> Double {
let path = shortestPath(to: destination, with: paths)
return path.compactMap { $0.weight }
.reduce(0, +)
}
}
测试
let graph = AdjacencyList()
let a = graph.createVertex(value: "A")
let b = graph.createVertex(value: "B")
let c = graph.createVertex(value: "C")
let d = graph.createVertex(value: "D")
let e = graph.createVertex(value: "E")
let f = graph.createVertex(value: "F")
let g = graph.createVertex(value: "G")
let h = graph.createVertex(value: "H")
graph.addDirectedEdge(from: a, to: b, weight: 1)
graph.addDirectedEdge(from: a, to: d, weight: 9)
graph.addDirectedEdge(from: a, to: c, weight: 2)
graph.addDirectedEdge(from: b, to: d, weight: 2)
graph.addDirectedEdge(from: c, to: d, weight: 8)
graph.addDirectedEdge(from: c, to: f, weight: 5)
graph.addDirectedEdge(from: d, to: g, weight: 9)
graph.addDirectedEdge(from: d, to: e, weight: 7)
graph.addDirectedEdge(from: e, to: d, weight: 5)
graph.addUndirectedEdge(between: e, and: f, weight: 4)
graph.addDirectedEdge(from: e, to: h, weight: 3)
let dijkstra = Dijkstra(graph: graph)
let pathsFromA = dijkstra.paths(from: a)
let path = dijkstra.shortestPath(to: e, with: pathsFromA)
for edge in path {
print("\(edge.source) -- \(edge.weight ?? 0) -- > \(edge.destination)")
}
// 结果
0: A -- 1.0 --> 1: B
1: B -- 2.0 --> 3: D
3: D -- 7.0 --> 4: E
首先用邻接表创建本篇文章例子的图,最终通过 Dijkstra 找到从 A 通往 E 的最小路径为:A --> B --> D --> E。
性能分析
迪克斯特拉算法的时间复杂度,主要取决于优先队列中元素的移除和插入。
优先队列中元素的移除和插总的时间是 O(log V)。在算法的实现中,我们还要遍历所有的顶点,时间为 O(E)。所以迪克斯特拉算法总的时间复杂度为 O(E log V)。
完整代码 >>
参考资料
Data Structures and Algorithms in Swift --- raywenderlich.com,如果想看原版书籍,请点击链接购买。
完
欢迎加入我管理的Swift开发群:536353151。