OpenCV--Python 图像平滑之中值平滑、双边滤波、联合双边滤波、导向滤波

1. 中值平滑

原理详解

  中值平滑，类似于卷积，也是一种邻域运算，但计算的不是加权求和，而是对邻域中的像素点按灰度值进行排序，然后选择该组中的中值作为输出的灰度值。

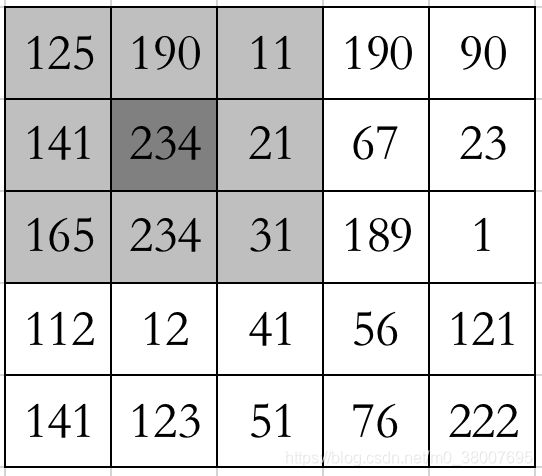
  比如，取以图像的位置 （1，1）为中心的 3X3 的邻域，对邻域中的像素点灰度值按从大到小进行排序，$[11,21,31,125,141,165,190,234,234]$ 可知，141是该组灰度值的中值，那么输出图像在位置（1，1）的值便为141，以此类推，得到输出图像的所有像素点的灰度值。对边界的处理可采用多种策略，而对边界进行镜像补充是较为理想的一种选择。

  中值滤波最重要的能力是去除椒盐噪声。椒盐噪声是指在图像传输系统中由于解码误差等原因，导致图像中出现孤立的白点或者黑点。

Python实现

  对于python实现的中值平滑，首先利用命令 $\mathrm{n}\mathrm{d}\mathrm{a}\mathrm{r}\mathrm{r}\mathrm{a}\mathrm{y}[r_1:r_2+1,c_1:c_2+1]$ 得到 $\mathrm{n}\mathrm{d}\mathrm{a}\mathrm{r}\mathrm{r}\mathrm{a}\mathrm{y}$ 从左上角至右下角的矩形区域，然后利用$\mathrm{N}\mathrm{u}\mathrm{m}\mathrm{p}\mathrm{y}$提供的函数median取该区域的中位数。

# -*- coding: utf-8 -*-
import random
import cv2 as cv
import numpy as np

def medianBlur(image, winSize):
    # 图像的高宽
    rows, cols = image.shape
    # 窗口的高宽均为奇数
    winH, winW = winSize
    halfWinH = (winH - 1) // 2
    halfWinW = (winW - 1) // 2
    # 中值滤波后的输出图像
    medianBlurImage = np.zeros(image.shape, image.dtype)
    for r in range(rows):
        for c in range(cols):
            # 判断边界
            rTop = 0 if r - halfWinH < 0 else r - halfWinH
            rBottom = rows - 1 if r + halfWinH > rows - 1 else r + halfWinH
            cLeft = 0 if c - halfWinW < 0 else c - halfWinW
            cRight = cols - 1 if c + halfWinW > cols - 1 else c + halfWinW
            # 取邻线
            region = image[rTop:rBottom+1, cLeft:cRight+1]
            # 求中值
            medianBlurImage[r][c] = np.median(region)
    return medianBlurImage

if __name__ == '__main__':
    image = cv.imread('img6.jpg', 0)
    cv.imshow('src', image)
    # 中值滤波
    medianBlurImage1 = medianBlur(image, (3,3))
    cv.imshow('3x3', medianBlurImage1)
    medianBlurImage2 = medianBlur(image, (15, 15))
    cv.imshow('15x15', medianBlurImage2)
    medianBlurImage3 = medianBlur(image, (25, 25))
    cv.imshow('25x25', medianBlurImage3)
    cv.waitKey(0)
    cv.destroyAllWindows()

  下图分别为添加了椒盐噪声的图像，3x3中值滤波后的图像，15x15中值滤波后的图像，25x25中值滤波后的图像。通过中值滤波去除了图像中的黑色孤立点，几乎看不到椒盐噪声的影响，并且随着中值平滑窗口的增加，椒盐噪声会完全消除。而且中值平滑后的效果并没有降低边缘的锐利程度，具有一定的保边作用。

OpenCV函数

dst = cv.medianBlur(src, ksize[, dst])

参数解释如下：

参数	解释
src	输入矩阵
dst	输出矩阵，其大小和数据类型与src相同
ksize	若为大于1的奇数，则窗口大小为kszie x ksize

Python示例代码

medianBlurImage = cv.medianBlur(image, 3)

总结

中值滤波适用于椒盐噪声，具有保边作用。

调用函数：dst = cv.medianBlur(src, ksize[, dst])

---

2. 双边滤波

原理详解

  均值平滑和高斯平滑本质上是计算每个位置的邻域加权和作为该位置的输出，只是这种运算可以用卷积实现，加权系数模版是通过卷积核逆时针翻转 $180^{\circ }$ 得到的。双边滤波则是根据每个位置的邻域，对该位置构建不同的权重模板，详细过程如下：

  首先，构建 $\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{H}\ast \mathrm{w}\mathrm{i}\mathrm{n}\mathrm{W}$ 的空间距离权重模板，与构建高斯卷积核的过程类似，$\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{H}$ 和 $\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{W}$ 均为奇数。
$$\mathbf{c}\mathbf{l}\mathbf{o}\mathbf{s}\mathbf{e}\mathbf{n}\mathbf{e}\mathbf{s}\mathbf{s}\mathbf{W}\mathbf{e}\mathbf{i}\mathbf{g}\mathbf{h}\mathbf{t}(h,w)=\exp (-\frac{(h-\frac{\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{H}-1}{2}{)}^2+(w-\frac{\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{W}-1}{2}{)}^2}{2{\sigma }_1^2})$$
其中 $0\le h<\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{H},0\le w<\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{W}$ ，且每个位置的空间距离权重模板是相同的。

  然后，构建$\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{H}\ast \mathrm{w}\mathrm{i}\mathrm{n}\mathrm{W}$ 的相似性权重模板，是通过$(r,c)$ 处的值与其邻域值的差值的指数衡量的。
$$\mathbf{s}\mathbf{i}\mathbf{m}\mathbf{i}\mathbf{l}\mathbf{a}\mathbf{r}\mathbf{i}\mathbf{t}\mathbf{y}\mathbf{W}\mathbf{e}\mathbf{i}\mathbf{g}\mathbf{h}\mathbf{t}(h,w)=\exp (-\frac{||I(r,c)-I(r+(h-\frac{\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{H}-1}{2}),c+(w-\frac{\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{W}-1}{2})|{|}^2}{2{\sigma }_1^2})$$

  最后，将 $\mathbf{c}\mathbf{l}\mathbf{o}\mathbf{s}\mathbf{e}\mathbf{n}\mathbf{e}\mathbf{s}\mathbf{s}\mathbf{W}\mathbf{e}\mathbf{i}\mathbf{g}\mathbf{h}\mathbf{t}$ 和 $\mathbf{s}\mathbf{i}\mathbf{m}\mathbf{i}\mathbf{l}\mathbf{a}\mathbf{r}\mathbf{i}\mathbf{t}\mathbf{y}\mathbf{W}\mathbf{e}\mathbf{i}\mathbf{g}\mathbf{h}\mathbf{t}$ 的对应位置相乘（即点乘），然后进行归一化，便可得到该位置的权重模板。将所得到的权重模板和该位置邻域的对应位置相乘，然后求和就得到该位置的输出值，和卷积运算的第二步操作类似。

Python实现

  通过定义函数 bfltGray 实现图像的双边滤波，其中参数 $I$ 代表图像矩阵且灰度值范围是 [0,1]，H，W分别代表权重模块的高和宽且均为奇数，sigma_g代表空间距离权重模板的标准差，sigma_d代表相似性权重模板的标准差，另 sigma_g > 1，sigma_d < 1效果会比较好，返回值是浮点型矩阵，代码如下：

import cv2 as cv
import numpy as np
import math

def getClosenessWeight(sigma_g, H, W):
    r, c = np.mgrid[0:H:1, 0:W:1]
    r -= (H - 1) // 2
    c -= (W - 1) // 2
    closeWeight = np.exp(-0.5*np.power(r, 2) + np.power(c, 2) / math.pow(sigma_g, 2))
    return closeWeight

def bfltGray(I, H, W, sigma_g, sigma_d):
    # 构建空间距离权重模板
    closenessWeight = getClosenessWeight(sigma_g, H, W)
    # 模板的中心点位置
    cH = (H - 1) // 2
    cW = (W - 1) // 2
    # 图像矩阵的行数和列数
    rows, cols = I.shape
    # 双边滤波后的结果
    bflGrayImage = np.zeros(I.shape, np.float32)
    for r in range(rows):
        for c in range(cols):
            pixel = I[r][c]
            # 判断边界
            rTop = 0 if r - cH < 0 else r - cH
            rBottom = rows - 1 if r + cH > rows - 1 else r + cH
            cLeft = 0 if c - cW < 0 else c - cW
            cRight = cols - 1 if c + cW > cols - 1 else c + cW
            # 权重模板作用的区域
            region = I[rTop:rBottom+1, cLeft:cRight+1]
            # 构建灰度值相似性的权重因子
            similarityWeightTemp = np.exp(-0.5*np.power(region-pixel, 2.0) / math.pow(sigma_d, 2))
            closenessWeightTemp = closenessWeight[rTop-r+cH:rBottom-r+cH+1, cLeft-c+cW:cRight-c+cW+1]
            # 两个权重模板相乘
            weightTemp= similarityWeightTemp * closenessWeightTemp
            # 归一化权重模板
            weightTemp = weightTemp / np.sum(weightTemp)
            # 权重模板和对应的邻域值相乘求和
            bflGrayImage[r][c] = np.sum(region * weightTemp)
    return bflGrayImage


if __name__ == '__main__':
    image = cv.imread('./img1.png', 0)
    print(image.shape)
    # 显示原图
    cv.imshow("image", image)
    # 将灰度值归一化
    image = image / 255
    # 双边滤波
    bfltImage = bfltGray(image, 51, 51, 30, 0.2)
    # 显示双边滤波的结果
    cv.imshow("bflt", bfltImage)

    gauImage = cv.GaussianBlur(image, (51, 51), 5)
    cv.imshow("gaussian", gauImage)
    blurImage = cv.blur(image, (51, 51))
    cv.imshow("blur", blurImage)
    cv.waitKey(0)
    cv.destroyAllWindows()

  下图分别为原图像，双边滤波（卷积核大小51x51，距离权重模板标准差30，相似性权重模板标准差0.2），高斯滤波（卷积核大小51x51，标准差5），均值滤波（核大小51x51）。显然，双边滤波对原图平滑的同时保持了物体的边缘，而高斯滤波和均值滤波虽然对图像有平滑作用，但是令原图的边缘更加模糊。

  与高斯平滑、均值平滑处理相比较，显然双边滤波在平滑作用的基础上，保持了图像中目标的边缘，但是由于每个位置都需要重新计算权重模板，所以会非常耗时（研究者有提出过双边滤波的快速算法）。

OpenCV函数

dst=cv.bilateralFilter(src, d, sigmaColor, sigmaSpace[, dst[, borderType]])

参数	解释
src	原图像矩阵
d	窗口大小
sigmaColor	相当于空间距离权重模板的标准差，尽量大
sigmaSpace	相当于相似性权重模板的标准差，尽量小

总结

  双边滤波可以在平滑图像的同时保证其中物体的边缘，但是平滑效果没有高斯滤波好，保持边缘的效果比中值滤波好，但是非常耗时（比中值滤波要耗时）。

  对有纹理的图像进行平滑处理时，希望将高斯平滑和双边滤波处理后的特性结合起来，即在平滑纹理的同时保留边缘，下文要介绍的联合双边滤波可以做到这一点。

---

3. 联合双边滤波

原理详解

  联合双边滤波与双边滤波类似。

  首先，对每个位置的邻域构建空间距离权重模板。与上文双边滤波构建空间距离权重模板一样。

  然后，构建相似性权重模板。这是与双边滤波唯一的不同之处，双边滤波是根据原图，对于每一个位置，通过该位置和其邻域的灰度值的差的指数来估计相似性；而联合双边滤波是首先对原图进行高斯平滑，根据平滑的结果，用当前位置及其邻域的值的差来估计相似性权重模板。

  接下来，空间距离权重模板和相似性权重模板点乘，然后归一化，作为最后的权重模板。最后将权重模板与原图（注意不是高斯平滑的结果）在该位置的邻域对应位置积的和作为输出值。整个过程只在第二步计算相似度权重模板时和双边滤波不同，但是对图像平滑的效果，特别是对纹理图像来说，却有很大的不同。

Python实现

  通过定义函数 joinBLF 实现联合双边滤波，其中构建空间距离权重模板的函数 getClosenessWeight 和双边滤波是一样的，参数 $\mathrm{I}$ 代表输入矩阵，注意这里不需要像双边滤波那样进行灰度值归一化；$\mathrm{H},\mathrm{W}$ 分别代表权重模板的高和宽，两者均为奇数；sigma_g 和 sigma_d 分别代表空间距离权重模板和相似性权重模板的标准差，这四个参数和双边滤波的定义是一样的。在双边滤波的实现代码中，并没有像卷积平滑那样对边界进行扩充，需要在代码中判断边界，为了省去判断边界的问题，在联合双边滤波的实现中对矩阵进行边界扩充操作，即参数 borderType 的含义，对于扩充边界的处理，这一点就类似于 OpenCV 实现的双边滤波，代码如下：

import cv2 as cv
import numpy as np
import math

def getClosenessWeight(sigma_g, H, W):
    r, c = np.mgrid[0:H:1, 0:W:1]
    r -= (H - 1) // 2
    c -= (W - 1) // 2
    closeWeight = np.exp(-0.5*np.power(r, 2) + np.power(c, 2) / math.pow(sigma_g, 2))
    return closeWeight

def joinBLF(I, H, W, sigma_g, sigma_d, borderType=cv.BORDER_DEFAULT):
    # 构建空间距离权重模板
    closenessWeight = getClosenessWeight(sigma_g, H, W)
    # 对I进行高斯平滑
    Ig = cv.GaussianBlur(I, (H, W), sigma_g)
    # 模板的中心点位置
    cH = (H - 1) // 2
    cW = (W - 1) // 2
    # 对原图和高斯平滑的结果扩充边界
    Ip = cv.copyMakeBorder(I, cH, cH, cW, cW, borderType)
    Igp = cv.copyMakeBorder(Ig, cH, cH, cW, cW, borderType)
    # 图像矩阵的行和列
    rows, cols = I.shape
    i, j = 0, 0
    # 联合双边滤波的结果
    jblf = np.zeros(I.shape, np.float64)
    for r in range(cH, cH+rows, 1):
        for c in range(cW, cW+cols, 1):
            # 当前位置的值
            pixels = Igp[r][c]
            # 当前位置的邻域
            rTop, rBottom = r-cH, r+cH
            cLeft, cRight = c-cW, c+cW
            # 从Igp中截取该邻域，用于构建相似性权重模板
            region = Igp[rTop:rBottom+1, cLeft:cRight+1]
            # 通过上述邻域，构建该位置的相似性权重模板
            similarityWeight = np.exp(-0.5 * np.power(region-pixels, 2.0) / math.pow(sigma_d, 2.0))
            # 相似性权重模板和空间距离权重模板相乘
            weight = closenessWeight * similarityWeight
            # 将权重模板归一化
            weight = weight / np.sum(weight)
            # 权重模板和邻域对应位置相乘并相加
            jblf[i][j] = np.sum(Ip[rTop:rBottom+1, cLeft:cRight+1] * weight)
            j += 1
        j = 0
        i += 1
    return jblf

if __name__ == '__main__':
    img = cv.imread('./img3.jpg', 0)
    cv.imshow('src', img)
    # 将8位图转换为浮点型
    fI = img.astype(np.float64)
    # 联合双边滤波，返回值的数据类型为浮点型
    jblf = joinBLF(img, 27, 27, 80, 5)
    # 转换为8位图
    jblf = np.round(jblf)
    jblf = jblf.astype(np.uint8)
    cv.imshow('jblf', jblf)
    cv.waitKey(0)
    cv.destroyAllWindows()

  对于函数 copyMakeBorder 的说明可以看 二维离散卷积的same卷积部分 或者 官方文档

OpenCV函数

dst=cv.ximgproc.jointBilateralFilter(joint, src, d, sigmaColor, sigmaSpace[, dst[, borderType]])

此函数的参数 src, d, sigmaColor, sigmaSpace 都与双边滤波一样，只介绍一下参数 joint, 这个参数就对应于原理详解部分的高斯平滑后的图像，Python示例如下：

img = cv.imread('./img3.jpg', 0)
cv.imshow('src', img)
# 均值平滑
img_mean = cv.blur(img, (27, 27), borderType=cv.BORDER_DEFAULT)
cv.imshow('mean', img_mean)
# 双边滤波
img_bilateral = cv.bilateralFilter(img, 27, 80, 5, borderType=cv.BORDER_DEFAULT)
cv.imshow('bilateral', img_bilateral)
# 联合双边滤波
img_gaussian = cv.GaussianBlur(img, (27, 27), 80, borderType=cv.BORDER_DEFAULT)
img_joint = cv.ximgproc.jointBilateralFilter(img_gaussian, img, 27, 80, 5, borderType=cv.BORDER_DEFAULT)
cv.imshow('joint', img_joint)

cv.waitKey(0)
cv.destroyAllWindows()

下图为原图，均值平滑，双边滤波，联合双边滤波后的图像。

如果出现错误 AttributeError: module 'cv2.cv2' has no attribute 'jointBilateralFilter' ，可使用以下命令安装 opencv-contrib-python 后可使用函数 jointBilateralFilter ，若通过以下命令解决不了问题，可自行查找解决办法。

pip3 install opencv-contrib-python

总结

  基于双边滤波和联合双边滤波，又提出了循环导向滤波，双边滤波是根据原图计算相似性权重模板的，联合双边滤波对其进行了改进，是根据图像的高斯平滑结果计算相似性权重模板的，而循环导向滤波，顾名思义，是一种迭代的方法，本质上是一种多次迭代的联合双边滤波，只是每次计算相似性权重模板的依据不一样——利用本次计算的联合双边滤波结果作为下一次联合双边计算相似度权重模板的依据。下面介绍不依赖于权重模板的保持边缘的滤波方法——导向滤波。

---

4. 导向滤波

原理详解

  导向滤波是 $\mathrm{K}\mathrm{a}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{H}\mathrm{e}$ 提出的。 导向滤波在平滑图像的基础上，有良好的保边作用，而且在细节增强等方面都有良好的表现，在执行时间上也比双边滤波快很多。

   输入： 导向图像 $I$ ，滤波输入图像 $p$ ，均值平滑的窗口半径 $r$，正则化参数 $ϵ$。利用导向滤波进行图像的平滑处理时，通常令 $p=I$。

   输出： 导向滤波结果 $q$

  $mea{n}_I=f_{mean}(I,r)$

  $mea{n}_p=f_{mean}(p,r)$

  $cor{r}_I=f_{mean}(I.\ast I,r)$

  $cor{r}_{Ip}=f_{mean}(I.\ast p,r)$

  $va{r}_I=cor{r}_I-mea{n}_I.\ast mea{n}_I$

  $co{v}_{Ip}=cor{r}_{Ip}-mea{n}_I.\ast mea{n}_p$

  $a=co{v}_{Ip}./(va{r}_I+ϵ)$

  $b=mea{n}_p-a.\ast mea{n}_I$

  $mea{n}_a=f_{mean}(a,r)$

  $mea{n}_b=f_{mean}(b,r)$

  $q=mea{n}_a.\ast I+mea{n}_b$

  其中 $f_{mean}$ 代表均值平滑；$.\ast$ 代表两个图像矩阵对应值相乘；$./$ 代表两个图像矩阵对应值相除。从伪代码中可以看出，多次使用了均值平滑。需要注意的是，$I$ 和 $q$ 均是归一化的图像矩阵，结果 $q$ 也是灰度值范围为 $[0,1]$ 的图像矩阵。

Python实现

  通过定义函数 guidedFilter 实现导向滤波，其中参数 I 代表输入的是灰度值归一到 $[0,1]$ 的浮点型矩阵， winSize 代表均值卷积核窗口尺寸，宽、高为奇数，eps代表正则化参数。返回值为灰度值范围在 $[0,1]$ 之间的图像矩阵，其中均值平滑可以使用Opencv中的函数 blur 或者 boxFilter。

import math
import cv2 as cv
import numpy as np

def guidedFilter(I, p, winSize, eps):
    # 输入图像的高，宽
    rows, cols = I.shape
    # I的均值平滑
    mean_I = cv.blur(I, winSize, borderType=cv.BORDER_DEFAULT)
    # p的均值平滑
    mean_p = cv.blur(p, winSize, borderType=cv.BORDER_DEFAULT)
    # I .* p 的均值平滑
    Ip = I * p
    mean_Ip = cv.blur(Ip, winSize, borderType=cv.BORDER_DEFAULT)
    # 协方差
    cov_Ip = mean_Ip - mean_I * mean_p
    mean_II = cv.blur(I*I, winSize, borderType=cv.BORDER_DEFAULT)
    # 方差
    var_I = mean_II - mean_I * mean_I
    a = cov_Ip / (var_I + eps)
    b = mean_p - a * mean_I
    # 对a和b进行均值平滑
    mean_a = cv.blur(a, winSize, borderType=cv.BORDER_DEFAULT)
    mean_b = cv.blur(b, winSize, borderType=cv.BORDER_DEFAULT)
    q = mean_a * I + mean_b
    return b

if __name__ == '__main__':
    image = cv.imread('./img7.jpg', 0)
    # 将图像进行归一化
    image_0_1 = image / 255.0
    # 显示原图
    cv.imshow('image', image)
    # 导向滤波
    result = guidedFilter(image_0_1, image_0_1, (9, 9), math.pow(0.2, 2.0))
    cv.imshow('guidedFilter', result)
	# 细节增强
    result_enhanced = (image_0_1 - result) * 5 + result
    result_enhanced = cv.normalize(result_enhanced, result_enhanced, 1, 0, cv.NORM_MINMAX)
    cv.imshow('result_enhanced', result_enhanced)
    # 保存导向滤波的结果
    result = result * 255
    result[result > 255] = 255
    result = np.round(result)
    result = result.astype(np.uint8)
    cv.imwrite('guidedFilter.jpg', result)
    
    cv.waitKey(0)
    cv.destroyAllWindows()

  在主函数中，需要注意导向滤波返回的是灰度值范围在 $[0,1]$ 之间的图像矩阵，如果想保存8位图，则首先乘以255，然后转换数据类型就可以了。对于导向滤波，可以利用图像的几何变换进行加速。

快速导向滤波

可以通过先缩小图像，然后再放大图像，对导向滤波进行加速，提高执行效率。

下图显示了原图、导向滤波后的图像和通过细节增强后的图像，细节增强后的图像可能会比较暗，可以使用伽马变换或者线性变换增加对比度或亮度。

OpenCV函数

dst=cv.ximgproc.guidedFilter(guide, src, radius, eps[, dst[, dDepth]])

附上关于导向滤波的文献

[1] K. He, J. Sun, and X. Tang. Guided image filtering. In ECCV, pages 1-14. 2010

[2] K. He, J. Sun, and X. Tang. Guided image filtering. TPAMI, 35(6): 1397-1409, 2013

---

总结

高斯平滑：dst=cv.GaussianBlur(src, ksize, sigmaX[, dst[, sigmaY[, borderType]]])

均值平滑：dst=cv.blur(src, ksize[, dst[, anchor[, borderType]]])

     dst = cv.boxFilter(src, ddepth, ksize[, dst[, anchor[, normalize[, borderType]]])

中值平滑：dst = cv.medianBlur(src, ksize[, dst])

双边滤波：dst=cv.bilateralFilter(src, d, sigmaColor, sigmaSpace[, dst[, borderType]])

联合双边滤波：dst=cv.ximgproc.jointBilateralFilter(joint, src, d, sigmaColor, sigmaSpace[, dst[, borderType]])

导向滤波：dst=cv.ximgproc.guidedFilter(guide, src, radius, eps[, dst[, dDepth]])

  至此，图像平滑的常用方法就介绍完了。图像平滑的方法多种多样，在实际应用中还要学会灵活运用，掌握其中的原理，并且和图像增强的方法结合使用能达到很好的效果。

---