1、工具箱的安装
参考网址:https://blog.csdn.net/qrlhl/article/details/52213135
EMD工具箱,下载地址为:http://perso.ens-lyon.fr/patrick.flandrin/emd.html,下载以后的名称是package_emd
时频分析工具箱:https://pan.baidu.com/share/init?surl=-jOdWceZebqnK6kzO2Hhyg,密码 stim,选择0.2的版本
下完以后把它们都放到MTALB安装目录的toolbox下,添加到工作路径
在MATLAB下运行
run install_emd.m
就可以啦。如果在安装之后,Matlab提示“cemdc2_fix.c等文件安装失败”,如果想让其编译成功则可以参考这篇文章:http://forum.vibunion.com/thread-79866-1-1.html,如果嫌麻烦的话,也可以不用修复,不会影响到使用EMD功能的。
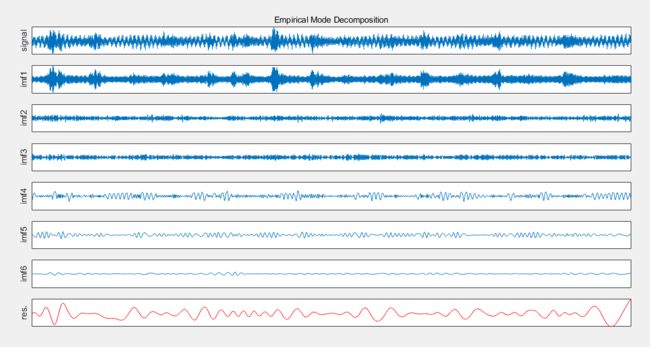
测试程序,会出来3个图:
fs = 1000;
ts = 1/fs;
t=0:ts:0.3;
z = sin(2*pi*10*t) + sin(2*pi*100*t);
imf=emd(z);
emd_visu(z,t,imf) % EMD专用画图函数
2、实例演示
load('temp_data.mat') %这边自己找一个波形数据就行,emd是针对波形的算法,对波形没有什么要求
close all
X=DATA.d; %波形的y值
t=DATA.t; %波形的x值
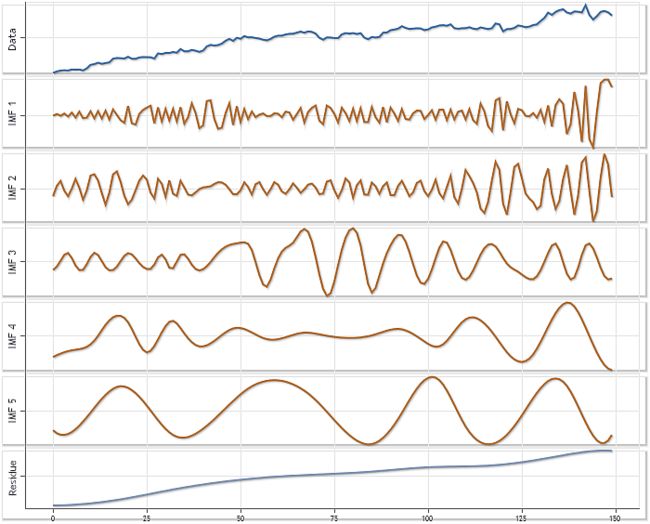
[imf,residual,info] = emd(X,'MAXITERATIONS',6);
emd_visu(X,t,imf(1:7,:))
3、emd原理简介
EMD其实就是一种对信号进行分解的方法,与傅里叶变换、小波变换的核心思想一致,大家都想将信号分解为各个相互独立的成分的叠加;只不过傅里叶变换以及小波变换都要求要有基函数,而EMD却完全抛开了基函数的束缚,仅仅依据数据自身的时间尺度特征来进行信号分解,具备自适应性。由于无需基函数,EMD几乎可以用于任何类型信号的分解,尤其是在非线性、非平稳信号的分解上具有明显的优势。
EMD 将任何给定数据分解为本质模态函数 (IMF),这些函数在分析上未被设定,而是由所分析的序列单独确定。在这种情况下,基函数从输入数据自适应地直接得出。从 EMD 生成的 IMF 应满足以下要求:
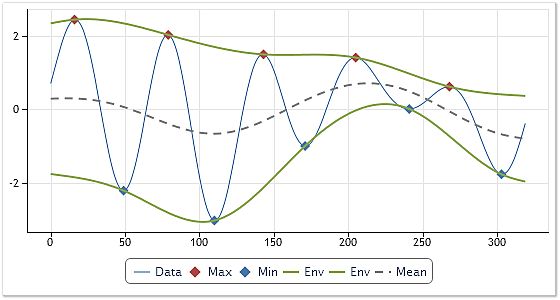
IMF 极值的数量(最大值和最小值的数量之和)与零穿越的数量必须相等或最多相差 1;
在 IMF 的任意点,局部最大值定义的包络线的平均值和局部最小值定义的包络线的平均值应等于零。
(这些分量是以某种形式合成的;它们的提取仅帮助更好地了解输入序列的结构,并且在很多情形中能够促进其分析。但不应该认为使用此方法获得的分量一定对应了实际物理过程)
为什么IMF一定要满足这两个条件呢?经黄锷等人的研究,满足这两个条件的信号都是单组分的,相当于序列的每一个点只有一个瞬时频率,无其他频率组分叠加。这就为后续的希尔伯特变换铺平了道路,也使得瞬时频率有了意义。
值得一提的是,EMD在数学上还有一些细节无法证明,但是EMD已经在工程领域取得了辉煌的成就
黄锷 (Norden E. Huang)提出的算法以产生序列的局部最大值和最小值所定义的平滑包络线,接着从初始序列减去这些包络线的平均值为基础。这要求识别所有局部极值,然后用三次样条曲线进一步将这些极值连接起来,以生成上下包络线。
4、emd分解的应用
除了计算频率谱以外,EMD 算法还可用于平滑序列。应该指出,在生成预测时,可以放弃一个或多个最高频率的分量。因此,高频噪声对预测的影响可得到抑制