关于逻辑回归的理解以及公式推导,可以看前面的文章
逻辑回归公式推导
逻辑回归
sigomoid function:
用梯度上升算法来求参数,求函数的最大值。
迭代步骤:
训练算法:求参数
主要步骤如下:
- 将数据转化成矩阵
- 求梯度
from numpy import *
def loadData(filename):
'''
读取文件
'''
datamat = []; labelmat = []
with open(filename) as f:
for line in f.readlines():
line_arr = line.strip().split()
#有1.0是因为有一个常数项
datamat.append([1.0, float(line_arr[0]), float(line_arr[1])])
labelmat.append(int(line_arr[2]))
return datamat, labelmat
datamat,labelmat = loadData('testSet.txt')
def sigmoid(inX):
'''
sigmoid函数
-inX:-wT·x
'''
return 1.0/(1+exp(-inX))
def gradAscent(dataMatIn,classLabels):
'''
梯度上升算法
dataMatIn:训练样本
classLabels:标签
'''
dataMatrix = mat(dataMatIn)
labelMat = mat(classLabels).transpose()
m,n = shape(dataMatrix)
alpha = 0.001
maxCycles = 500
#weights are parameters' vector
weights = ones((n,1))
for k in range(maxCycles):
h = sigmoid(dataMatrix*weights)
error = (labelMat - h)
#推导过程如下:
weights = weights +alpha*dataMatrix.transpose()*error
return weights
推导:因为代价函数的梯度已知:
weights = gradAscent(datamat,labelmat)
import matplotlib
import matplotlib.pyplot as plt
from numpy import *
def plot_fit(data, labelMat, weights):
'''
画图,得到分界线
data:训练样本
labelMat:标签矩阵
'''
dataArr = array(data)
n = shape(dataArr)[0]
x_cord1 = []; y_cord1 = []
x_cord2 = []; y_cord2 = []
for i in range(n):
if int(labelMat[i]) == 1:
x_cord1.append(dataArr[i,1]); y_cord1.append(dataArr[i,2])
else: x_cord2.append(dataArr[i,1]); y_cord2.append(dataArr[i,2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(x_cord1, y_cord1, s = 30, c = 'red', marker='s')
ax.scatter(x_cord2, y_cord2, s = 30, c = 'green')
x = arange(-3.0, 3.0, 0.1)
y = ((-weights[0]- weights[1] * x)/weights[2]).transpose()
ax.plot(x, y)
plt.xlabel('X1');
plt.ylabel('X2');
plt.show()
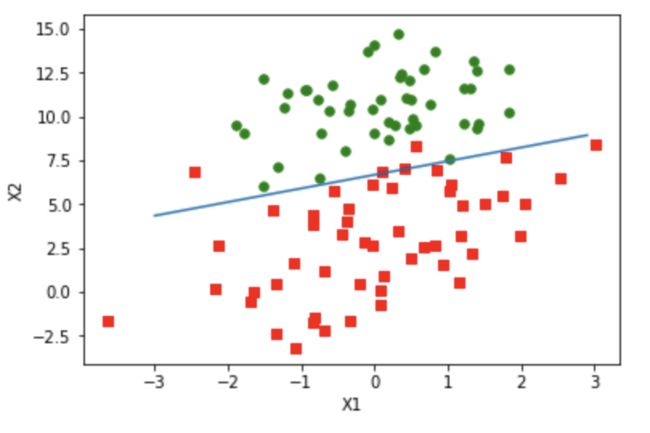
plot_fit(datamat,labelmat,weights)
梯度下降法分类效果还可以,100个样本分类错误4个,但是计算量太大了,计算了300次乘法,需要进一步改进算法。
随机梯度上升
梯度上升每次更新回归系数,都需要遍历整个数据集,一旦特征数量很大,计算复杂度太高了,改进方法叫随机梯度上升算法,每次选择一个样本点来更新回归系数
def stocGradAscent0(dataMatrix,classLabels):
'''
随机梯度上升算法
dataMatrix:训练样本
calssLabels:标签
output:参数值
'''
m,n = shape(dataMatrix)
alpha = 0.01
weights = ones(n)
for i in range(m):
h = sigmoid(sum(dataMatrix[i]*weights))
error = classLabels[i] - h
weights = weights + alpha*error*array(dataMatrix[I])
return weights
weight2 = stocGradAscent0(datamat,labelmat)
推导过程:
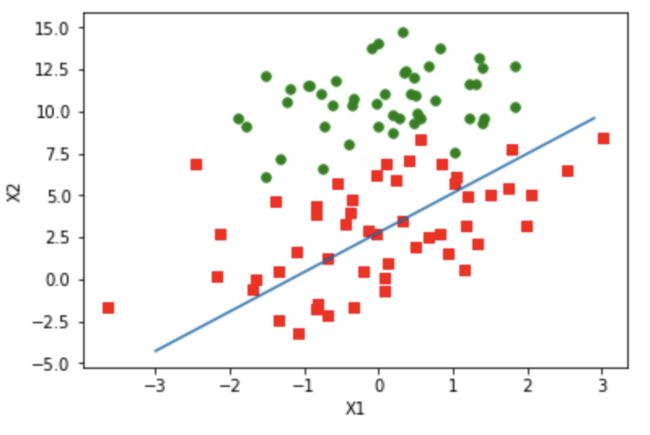
plot_fit(datamat,labelmat,weight2)
结果显示分类效果比较差,是因为迭代次数不确定导致参数还未达到稳定。可以对上述代码进行进一步修改
def stocGradAscent1(dataMatrix,classLabels,numIter = 150):
'''
改进的随机梯度上升算法
'''
m,n = shape(dataMatrix)
weights = ones(n)
#迭代次数
for j in range(numIter):
dataIndex = range(m)
#样本数量
for i in range(m):
#每次调整a,why?
alpha = 0.01+4/(1.0+j+i)
#uniform-->生成[x,y)之间的随机实数
randIndex = int(random.uniform(0,len(dataIndex)))
h = sigmoid(sum(dataMatrix[randIndex]*weights))
error = classLabels[randIndex] -h
weights = weights + alpha*error*array(dataMatrix[randIndex])
return weights
'''
1.不明白为什么每次需要调整alpha
2.随机选择样本可以减少周期波动
'''
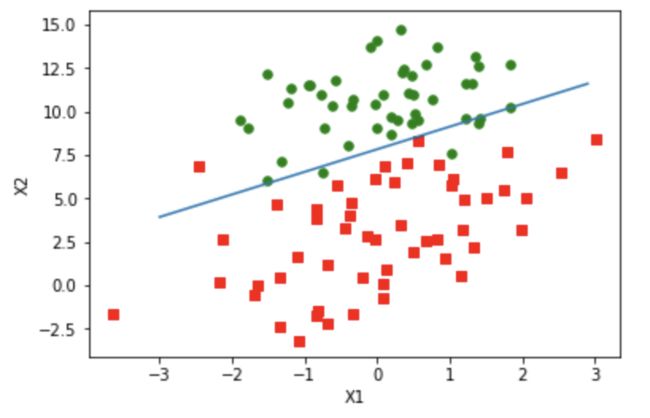
weights3 = stocGradAscent1(datamat,labelmat,10)
plot_fit(datamat,labelmat,weights3)
疝气病预测病马死亡率
用医院检测疝气病的指标,来预测病马的死亡率
数据预处理:缺失值处理
- 用特征均值填补
- 用特殊值填补,比如-1
- 忽略这部分样本
- 用类似样本均值填补
- 用机器学习算法来预测
具体做法:
- 选一个实数值替换,选0
- 标签缺失,需要丢弃数据
数据来源
def getDateSet(filepath):
'''
获得训练集和测试集
'''
import numpy as np
with open(filepath) as f:
file = f.readlines()
arr = []
dataSet = [];Labels=[]#训练集和标签集
for x in file:
mid = x.strip().split('\t')
vector = list(map(lambda x:float(x),mid))
arr.append(vector)
#用numpy提取数据集以及标签集,加一个x0项
mid2 = np.array(arr)
x0 = array([1]*len(file))
dataSet = np.column_stack((x0,mid2[:,:-1]))
Labels =mid2[:,-1]
return dataSet,Labels
trainingdataSet,trainingLabels = getDateSet('./horseColicTraining.txt')
testdataSet,testLabels = getDateSet('./horseColicTest.txt')
stocGradAscent1(trainingdataSet,trainingLabels,500)
array([ 2.88523241e+00, 4.60371241e+01, -3.44351209e+00, 1.81776542e+00,
-1.22312262e+00, -4.51162382e-02, -1.26815180e+01, -5.19715412e+00,
-1.62249176e+01, 1.69815852e+00, -1.42154178e+01, 2.51022948e+01,
-1.01675395e+01, 3.62858014e+01, -5.73351142e+00, -7.52889830e+00,
8.52370700e+00, -9.93327494e+00, -1.10860304e+00, 1.43608141e+00,
-2.06483905e+00, -5.98332914e+00])
#得到参数
weights = stocGradAscent1(trainingdataSet,trainingLabels,500)
#测试,计算w^tx
result = mat(testdataSet)*mat(weights).T
#sigmoid参数z,是-w^Tx的计算结果,sig
z = result.tolist()
sig = list(map(lambda x:sigmoid(x[0]),result.tolist()))
def classifyVector(x):
'''
sigmoid函数计算结果
'''
if x >0.5:
return 1.0
else:
return 0.0
#逻辑回归的预测结果
lg_result = [classifyVector(x) for x in sig]
#标签集转列表
testLabels.tolist()
#将预测结果和真实结果zip打包成元组n
zipped = zip(lg_result,testLabels.tolist())
n = list(zipped)
#计算分类错误率
errorRate = len([x for x in n if x[0]-x[1]!=0])/len(n)
上述代码合并如下:
def errorTest():
'''
错误率计算函数
weights:逻辑回归模型参数
'''
#数据集准备
trainingdataSet,trainingLabels = getDateSet('./horseColicTraining.txt')
testdataSet,testLabels = getDateSet('./horseColicTest.txt')
#得到参数
weights = stocGradAscent1(trainingdataSet,trainingLabels,10)
#测试,计算w^tx
result = mat(testdataSet)*mat(weights).T
#sigmoid参数z,是-w^Tx的计算结果,sig
z = result.tolist()
sig = list(map(lambda x:sigmoid(x[0]),result.tolist()))
#逻辑回归的预测结果
lg_result = [classifyVector(x) for x in sig]
#标签集转列表
testLabels.tolist()
#将预测结果和真实结果zip打包成元组n
zipped = zip(lg_result,testLabels.tolist())
n = list(zipped)
#计算分类错误率
errorRate = len([x for x in n if x[0]-x[1]!=0])/len(n)
print('错误率:%f'%errorRate)
return errorRate
errorTest()
错误率:0.283582
0.2835820895522388
def multiTest():
numTests = 10;errorSum=0.0
for k in range(numTests):
errorSum += errorTest()
print('经过10次迭代后平均错误率:%f'%(float(errorSum/numTests)))
multiTest()
错误率:0.268657
错误率:0.492537
错误率:0.328358
错误率:0.253731
错误率:0.268657
错误率:0.417910
错误率:0.358209
错误率:0.567164
错误率:0.283582
错误率:0.328358
经过10次迭代后平均错误率:0.356716
代码整理
def sigmoid(inX):
'''
sigmoid函数
-inX:-wT·x
'''
return 1.0/(1+exp(-inX))
def stocGradAscent1(dataMatrix,classLabels,numIter = 150):
'''
改进的随机梯度上升算法
'''
m,n = shape(dataMatrix)
weights = ones(n)
#迭代次数
for j in range(numIter):
dataIndex = range(m)
#样本数量
for i in range(m):
#每次调整a,why?
alpha = 0.01+4/(1.0+j+i)
#uniform-->生成[x,y)之间的随机实数
randIndex = int(random.uniform(0,len(dataIndex)))
h = sigmoid(sum(dataMatrix[randIndex]*weights))
error = classLabels[randIndex] -h
weights = weights + alpha*error*array(dataMatrix[randIndex])
return weights
def getDateSet(filepath):
'''
获得训练集和测试集
'''
import numpy as np
with open(filepath) as f:
file = f.readlines()
arr = []
dataSet = [];Labels=[]#训练集和标签集
for x in file:
mid = x.strip().split('\t')
vector = list(map(lambda x:float(x),mid))
arr.append(vector)
#用numpy提取数据集以及标签集,加一个x0项
mid2 = np.array(arr)
x0 = array([1]*len(file))
dataSet = np.column_stack((x0,mid2[:,:-1]))
Labels =mid2[:,-1]
return dataSet,Labels
def classifyVector(x):
'''
sigmoid函数计算结果分类
'''
if x >0.5:
return 1.0
else:
return 0.0
if __name__ =="__main__":
multiTest()
错误率:0.313433
错误率:0.283582
错误率:0.462687
错误率:0.626866
错误率:0.328358
错误率:0.268657
错误率:0.343284
错误率:0.328358
错误率:0.268657
错误率:0.298507
经过10次迭代后平均错误率:0.352239
小结
学习了逻辑回归算法,愈发感受到只看一本书效果并不好,而且《机器学习实战》一书缺陷明显,代码陈旧复杂,推导过程简陋,属于名副其实的入门书籍。有时候照着书上的代码操作结果就是出不来,令人非常恼火。好了,关于这一章的内容,有以下几个注意事项:
对于逻辑回归模型的本质:是一个回归模型嵌套在sigmoid函数中,模型借助其阶跃的特点,对样本进行二分类,其问题核心在于求解模型中的参数;从概率的角度来看,由于结果只有0,1,我们认为在拥有数据集的前提下,这些数据往往被取到的概率较大,而概率大小取决于使其取到这些值的参数决定,所以选择某个参数,使得取到数据集的概率最大,这种参数估计方法叫最大似然估计法。关于参数估计,可以使用梯度下降法进行。
随着学习的深入,更加觉得机器学习并非易事,从数据清洗-特征工程-模型选择-算法优化,这些都包含着高深的学问,此外,还需要有一定的数学基础以及编程能力。不禁感慨一句:
路漫漫其修远兮,吾将上下而求索。