最长公共子序列问题

问题描述：字符序列的子序列是指从给定字符序列中随意地（不一定连续）去掉若干个字符（可能一个也不去掉）后所形成的字符序列。令给定的字符序列X=“x0，x1，…，xm-1”，序列Y=“y0，y1，…，yk-1”是X的子序列，存在X的一个严格递增下标序列<i0，i1，…，ik-1>，使得对所有的j=0，1，…，k-1，有xij=yj。例如，X=“ABCBDAB”，Y=“BCDB”是X的一个子序列。

解决方法：

1、穷举法：针对序列x中所有的子序列(共2^m个)，在Y序列中寻列是否存在相同序列，并找出其中最大的序列。这种方法的时间复杂度为O(2^m*2^n)。

2、动态规划法：引进一个二维数组c[][]，用c[i][j]记录X[i]与Y[j] 的LCS 的长度，b[i][j]记录c[i][j]是通过哪一个子问题的值求得的，以决定搜索的方向。可以通过以下公式来计算从c[i][j]的值。

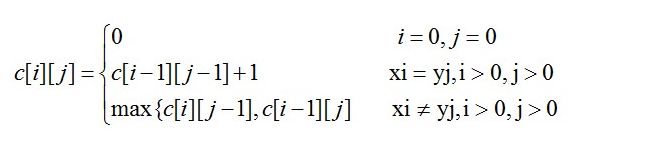
复杂度分析：

时间复杂度：O(m*n);

空间复杂度：O(m*n);

代码：

 1 #include "stdafx.h"

 2 #include <iostream>

 3 #include <string>

 4 #define MAXLEN 100

 5 using namespace std;

 6 

 7 void GetLCSLen(string str1, string str2,int m,int n,int c[][MAXLEN],int b[][MAXLEN])

 8 {

 9     int i, j;

10     for (i = 0; i <= m; i++)

11         c[i][0] = 0;

12     for (j = 1; j <= n; j++)

13         c[0][j] = 0;

14     

15     for (i = 1; i <= m; i++)

16     {

17         for (j = 1; j <= n; j++)

18         {

19             if (str1[i - 1] == str2[j - 1])

20             {

21                 c[i][j] = c[i - 1][j - 1] + 1;

22                 b[i][j] = 0;

23             }

24             else

25             {

26                 if (c[i - 1][j] >= c[i][j - 1])

27                 {

28                     c[i][j] = c[i - 1][j];

29                     b[i][j] = 1;

30                 }

31                 else

32                 {

33                     c[i][j] = c[i][j - 1];

34                     b[i][j] = 2;

35                 }

36             }

37         }

38     }

39 }

40 

41 void PrintLCS(int b[][MAXLEN], string x, int i, int j)  //递归回溯最长子序列

42 {

43     if (i == 0 || j == 0)

44         return;

45     if (b[i][j] == 0)

46     {

47         PrintLCS(b, x, i - 1, j - 1);

48         cout<<x[i-1];

49     }

50     else if (b[i][j] == 1)

51         PrintLCS(b, x, i - 1, j);

52     else

53         PrintLCS(b, x, i, j - 1);

54 }

55 

56 int _tmain(int argc, _TCHAR* argv[])

57 {

58     string s1 = "ABCBDAB";

59     string s2 = "BDCABA";

60     int strlen1 = s1.size();

61     int strlen2 = s2.size();

62     int b[MAXLEN][MAXLEN];

63     int c[MAXLEN][MAXLEN]; 

64     GetLCSLen(s1,s2,strlen1,strlen2,c,b);

65     cout << c[strlen1][strlen2] << endl;  //输出最长子序列长度

66     PrintLCS(b,s1,strlen1,strlen2);

67     return 0;

68 }

运行结果：

参考资料：

1、http://blog.csdn.net/v_july_v/article/details/6695482

2、http://blog.csdn.net/yysdsyl/article/details/4226630