前言
matlab自带的小波分析工具非常全！实际工作中直接用即可。但是刚开始使用会遇到挫折：它的函数太多，并且它们的"名称、功能、配套使用"等要求都有些"相近"，很容易导致糊涂！因此本文的总结与配套实例很具有参考价值！
下面先列举3条关键理解，后面会用到：
- 小波分解，分解到的"不是频率域"！可以抽象理解为"小波域"，但其实没有实际内涵！傅里叶变换到频率域是有实际内涵的；
- 小波分解得到的"小波系数"是"没有量纲"的！它其实是"没有实际意义的数"，需要做系数重构才能从"小波域"再转回到"时域"；
- "系数重构"与"重构信号"不是一个东西！系数重构就是把无量纲的小波分解系数变回到有意义的"时域"；"重构信号"就是把分解的完整恢复回去。
几种函数的说法与适用处
下面介绍最容易让人糊涂的matlab一些自带函数的说法与用途(都是针对离散小波变换)，不同的函数有不同的适用处于搭配函数.
分解与重构/恢复信号：
- 1级分解与重构原始信号函数为: dwt和dwt2 与 idwt和idwt2；
- 多级(包括1级)分解与重构原始信号函数为: wavedec和wavedec2 与 waverec和waverec2；所以wavedec可涵盖dwt。
系数重构：需理解其作用 √ √ √
1级分解的系数重构用函数的是: upcoef和upcoef2；
多级分解的系数重构用函数的是: wrcoef和wrcoef2。
系数提取：
- 多级分解低频近似系数提取：appcoef和appcoef2；
- 多解分解高频细节系数提取：detcoef和detcoef2。
说明："系数提取"只有"多级分解"才会用的到！ 1级分解是不需要"系数提取"的！因为就分成了低频和高频2个部分，直接用1维或2维分解函数的返回结果就行了！所以：多级分解的系数提取，就相当于1级分解后的返回结果的直接画图。
上面就是容易搞混的几个操作与使用搭配。
还是要着重强调一点：用自带的函数做完"小波分解"后，得到的"小波系数"是"没有量纲"的！可以理解为原始信号域映射到小波域(小波域不是什么具体的东西，只是为了方便理解)！只有把分解出来的"小波系数"再做"系数重构"后，才能回到原始的信号域，得到原始信号的不同的低频和高频子信号成分(还是时域的显示)。
下面我们先给出具体的例子(一维离散数据)，再总结每个函数具体的语法：
- 例子1：一维信号1级分解(dwt)、系数重构(upcoef)、重构/恢复信号(idwt)：
clc; clear;
% 导入自带的一个一维电压信号, 取前4096个点
load leleccum;
s = leleccum(1:4096);
% 一级"分解": 时域 → 小波域
% 说明: 2个"系数(低+高)"的尺寸全部是一半 2048
% 命令: dwt
[cA1,cD1] = dwt(s,'haar');
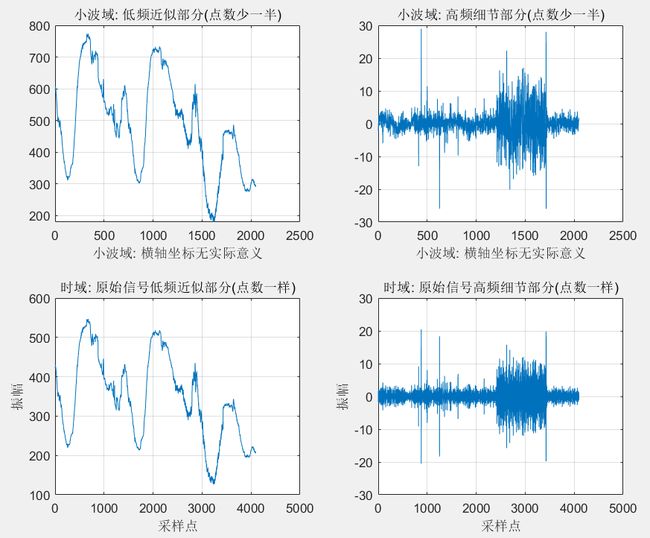
figure(1);
subplot(2,2,1); plot(cA1); title('小波域: 低频近似部分(点数少一半)'); grid on;
xlabel('小波域: 横轴坐标无实际意义');
subplot(2,2,2); plot(cD1); title('小波域: 高频细节部分(点数少一半)'); grid on;
xlabel('小波域: 横轴坐标无实际意义');
% 1级分解系数"重构": 小波域 → 时域
% 说明: 2个"子信号(低+高)"的尺寸全部和原始大小一样 4096！！
% 命令: upcoef
A1 = upcoef('a',cA1,'haar',1);
D1 = upcoef('d',cD1,'haar',1);
subplot(2,2,3); plot(A1); title('时域: 原始信号低频近似部分(点数一样)'); grid on;
xlabel('采样点'); ylabel('振幅');
subplot(2,2,4); plot(D1); title('时域: 原始信号高频细节部分(点数一样)'); grid on;
xlabel('采样点'); ylabel('振幅');
% 重构原始信号: 参数用的还是分解出的系数
% 命令: idwt
s_rec = idwt(cA1,cD1,'haar');
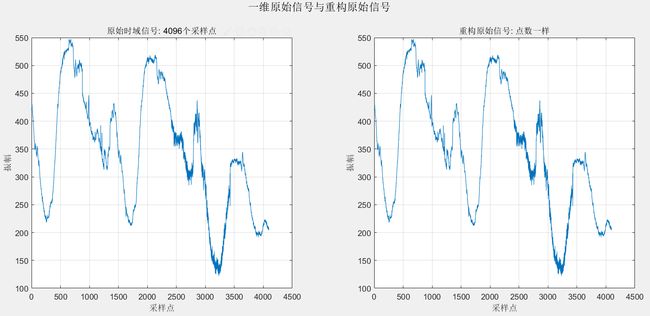
figure(2);
subplot(1,2,1); plot(s); title('原始时域信号: 4096个采样点'); grid on;
xlabel('采样点'); ylabel('振幅');
subplot(1,2,2); plot(s_rec); title('重构原始信号: 点数一样'); grid on;
xlabel('采样点'); ylabel('振幅');
suptitle('一维原始信号与重构原始信号');
figure(1)效果：
图1：一维1级小波(域)系数图像与系数重构时域子信号
figure(2)效果：
图2：原始信号与一维1级分解后重构信号对比
- 例子2：一维信号多级分解(wavedec)、系数重构(wrcoef)、系数提取(appcoef + detcoef)、重构/恢复信号(idwt)：
clc; clear;
% 导入自带的一个一维电压信号, 取前4096个点
load leleccum;
s = leleccum(1:4096);
% 多尺度/级分解:
% 命令: wavedec
[C,L]=wavedec(s,3,'db1');
% 系数提取: 提取经过变换之后的信号: 小波域下的低频系数(近似信息)和高频系数(细节信号), 即"时域→小波域"!
% 说明: 系数提取是多级分解才用！1级分解有就分成2个部分，不需要提取。
% 命令: appcoef低频系数提取; detcoef高频系数提取
cA3=appcoef(C,L,'db1',3); % 低: 3表示第三层
cD3=detcoef(C,L,3);
cD2=detcoef(C,L,2);
cD1=detcoef(C,L,1); % 3个高: 最后的数字表示的是层数
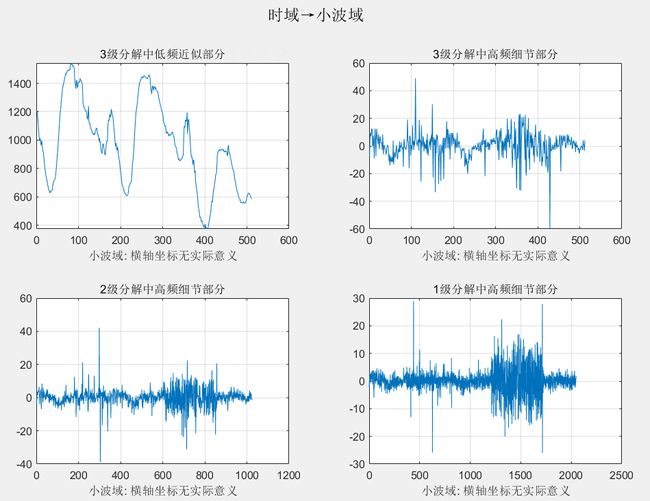
figure(1)
% 4个部分长度不一样！
subplot(2,2,1); plot(cA3); title('3级分解中低频近似部分'); grid on; % 长度 1/2^3 = 1/8
xlabel('小波域: 横轴坐标无实际意义');
subplot(2,2,2); plot(cD3); title('3级分解中高频细节部分'); grid on; % 长度 1/2^3 = 1/8
xlabel('小波域: 横轴坐标无实际意义');
subplot(2,2,3); plot(cD2); title('2级分解中高频细节部分'); grid on; % 长度 1/2^2 = 1/4
xlabel('小波域: 横轴坐标无实际意义');
subplot(2,2,4); plot(cD1); title('1级分解中高频细节部分'); grid on; % 长度 1/2^1 = 1/2
xlabel('小波域: 横轴坐标无实际意义');
suptitle('时域→小波域');
% 多级重构系数: 从小波域还原出信号高频部分的子信号, 即从"小波域→时域"！
% 命令: wrcoef 参数中a是低频, d是高频
A3=wrcoef('a',C,L,'db1',3); % 低
D3=wrcoef('d',C,L,'db1',3);
D2=wrcoef('d',C,L,'db1',2);
D1=wrcoef('d',C,L,'db1',1); % 3个高
figure(2)
subplot(2,2,1); plot(A3); title('原始信号中的低频信号成分'); grid on;
xlabel('采样点'); ylabel('振幅');
subplot(2,2,2); plot(D3); title('原始信号中的高频信号成分1'); grid on;
xlabel('采样点'); ylabel('振幅');
subplot(2,2,3); plot(D2); title('原始信号中的高频信号成分2'); grid on;
xlabel('采样点'); ylabel('振幅');
subplot(2,2,4); plot(D1); title('原始信号中的高频信号成分3'); grid on;
xlabel('采样点'); ylabel('振幅');
suptitle('小波域→时域');
% 重构原始信号: 滤波后单纯的恢复原始信号
% 命令: waverec
s_rec = waverec(C,L,'db1');
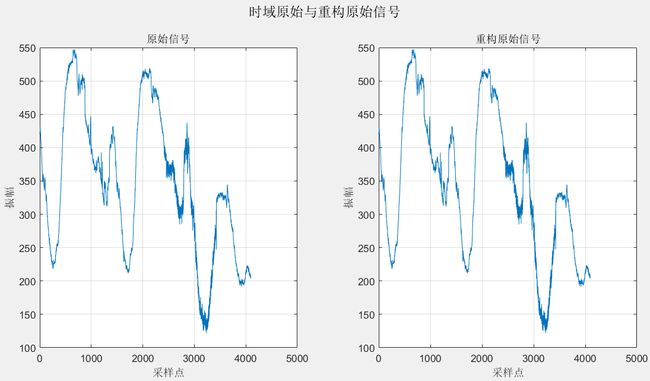
figure(3);
subplot(1,2,1); plot(s); title('原始信号'); grid on;
xlabel('采样点'); ylabel('振幅');
subplot(1,2,2); plot(s_rec); title('重构原始信号'); grid on;
xlabel('采样点'); ylabel('振幅');
suptitle('时域原始与重构原始信号');
figure(1)效果：
图3：一维多级分解后小波(域)系数图像
figure(2)效果：
图4：一维多级分解后系数重构时域子信号
figure(3)效果：
图5：原始信号与一维多级分解后重构信号对比
函数语法总结
语法总结按照上面的2个例子(一维离散数据)进行。
（1）首先总结例1中的函数语法：
- 一维1级分解函数：dwt
[cA1,cD1] = dwt(x,'wavename');
% dwt参数：x是原始信号，'wavename'是自己选的小波基函数(例如'haar')
% 左边返回值：cA1低频近似系数，cD1高频细节系数。
- 一维1级系数重构函数：upcoef
A1 = upcoef('a', cA1, 'wavename', 1); % 低频系数重构
D1 = upcoef('d', cD1, 'wavename', 1); % 高频系数重构
% upcoef参数：'a'表示低频近似/'d'表示高频细节，cA1与cD1系数，1就是当前是1解分解(不变);
% 左边返回值：A1是低频近似系数的重构结果，D1是高频细节系数的重构结果。
- 一维1级分解重构/恢复信号函数：idwt
s_rec = idwt(cA1,cD1,'wavename');
% idwt参数：cA1和cD1就是dwt分解得到的低频近似和高频细节的系数；
% 左边返回值：s_rec就是重构/恢复的原始信号。
（2）总结例2中的函数语法：
- 一维多级分解函数：wavedec
[C,L] = wavedec(s, N, 'wavename');
% wavedec参数：s是原始信号，N是分解级数，'wavename'小波基函数；
% 左边返回值：C是小波分解后的各个系数，L是相应小波系数的个数；
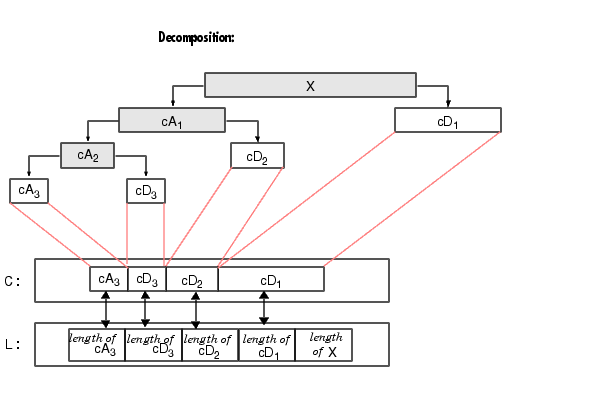
这个函数的返回值可能凭语言不好理解，直接看图6示意图就很好理解。注意到：C中是所有分解出来的东西(系数)的一个大汇总，即都在一个大矩阵里！所以就需要从C中把各个系数提取出来。
图6：wavedec返回值C和L的含义示意图
- 一维多级系数提取函数：appcoef与detcoef
% 以3级分解为例：
[C,L] = wavedec(s,3,'db1');
% 各级系数提取：
% 最后剩的那个低频近似部分(1个)的系数提取：appcoef
cA3 = appcoef(C, L, 'wavename', N);
% appcoef参数：C和L就是上面分解出来的东西，'wavename'和分解用的小波基一致，N和分解的级数一致；
% 左边返回值：最后那个低频近似的系数(从C和L中提取出来了)。
% 每一级中的高频细节部分(N个)的系数提取：detcoef
cD3 = detcoef(C, L, 3);
cD2 = detcoef(C, L, 2);
cD1 = detcoef(C, L, 1);
% detcoef参数：C和L和同意，后面的数字就是分解的层数；
% 左边返回值：每一级高频近似部分的系数(从C和L中提取出来)
说明：分解N级，要做N个高频细节部分的的系数提取，低频近似只用做一次！
- 一维多级系数重构函数：wrcoef
% 以3级分解为例：
[C,L] = wavedec(s,3,'db1');
% 直接上实例说明：'wavename'用的是'db1'
A3 = wrcoef('a',C,L,'db1',3); % 最后那个低频近似部分的系数重构
D3 = wrcoef('d',C,L,'db1',3); % 3级高频细节部分系数重构
D2 = wrcoef('d',C,L,'db1',2); % 2级高频细节部分系数重构
D1 = wrcoef('d',C,L,'db1',1); % 1级高频细节部分系数重构
% wrcoef参数：'a'或'd'代表"低频近似"或"高频细节"，C和L同意，最后的数字是该部分所在的级数；
% 左边返回指：各个部分系数重构的结果。
说明：分解N级，要做N个高频细节部分的的系数重构，低频近似只用做一次！
- 一维多级分解重构/恢复信号函数：waverec
s_rec = waverec(C,L,'wavename');
% waverec参数：C和L还是同意，'wavename'和上面用的小波基保持一致；
% 左边返回值：s_rec就是重构/恢复的原始信号。
注意：重构/恢复原始信号，用的是分解得到的系数！而不是系数重构后的东西。
至此，一维离散小波1级和多级分解所有会用到的函数就都介绍完毕了！以表总结：
| 一维1级分解 | 一维多级分解 | |
|---|---|---|
| 分解函数 | dwt | wavedec |
| 系数提取函数 | 不需要 | appcoef 和 detcoef |
| 系数重构函数 | upcoef | wrcoef |
| 重构/恢复信号函数 | idwt | waverec |