最后的日子-训练2
A - Solve equation
Time Limit:1000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u
Description
You are given two positive integers A and B in Base C. For the equation:
We know there always existing many non-negative pairs (k, d) that satisfy the equation above. Now in this problem, we want to maximize k.
For example, A="123" and B="100", C=10. So both A and B are in Base 10. Then we have:
(1) A=0*B+123
(2) A=1*B+23
As we want to maximize k, we finally get one solution: (1, 23)
The range of C is between 2 and 16, and we use 'a', 'b', 'c', 'd', 'e', 'f' to represent 10, 11, 12, 13, 14, 15, respectively.
Input
The first line of the input contains an integer T (T≤10), indicating the number of test cases.
Then T cases, for any case, only 3 positive integers A, B and C (2≤C≤16) in a single line. You can assume that in Base 10, both A and B is less than 2^31.
Output
Sample Input
Sample Output
#include <stdio.h> #include <string.h> #include <algorithm> using namespace std; int t,a,b,c,k,d,len; char s1[100],s2[100]; int set(char *s) { len = strlen(s); int ans = 0; for(int i = 0;i<len;i++) { int tem; if(s[i]>='0' && s[i]<='9') tem = s[i]-'0'; else tem = s[i]-'a'+10; ans = ans*c+tem;//进制转换 } return ans; } int main() { scanf("%d",&t); while(t--) { scanf("%s%s%d",s1,s2,&c); a = set(s1); b = set(s2); int tem = a/b; printf("(%d,%d)\n",tem,a-tem*b); } return 0; }
B - Bin & Jing in wonderland
Time Limit:1000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u
Description
Bin has a dream that he and Jing are both in a wonderland full of beautiful gifts. Bin wants to choose some gifts for Jing to get in her good graces.
There are N different gifts in the wonderland, with ID from 1 to N, and all kinds of these gifts have infinite duplicates. Each time, Bin shouts loudly, “I love Jing”, and then the wonderland random drop a gift in front of Bin. The dropping probability for gift i (1≤i≤N) is P(i). Of cause, P(1)+P(2)+…+P(N)=1. Bin finds that the gifts with the higher ID are better. Bin shouts k times and selects r best gifts finally.
That is, firstly Bin gets k gifts, then sorts all these gifts according to their ID, and picks up the largest r gifts at last. Now, if given the final list of the r largest gifts, can you help Bin find out the probability of the list?
Input
The first line of the input contains an integer T (T≤2,000), indicating number of test cases.
For each test cast, the first line contains 3 integers N, k and r (1≤N≤20, 1≤k≤52, 1≤r≤min(k,25)) as the description above. In the second line, there are N positive float numbers indicates the probability of each gift. There are at most 3 digits after the decimal point. The third line has r integers ranging from 1 to N indicates the finally list of the r best gifts’ ID.
Output
Sample Input
Sample Output
题意:给你N个数(从1--N)且P(1)+P(2)+…+P(N)=1,题目说你可以叫k个礼物,礼物是从小到大按照ID排序的,最后取r个礼物, 问你最后取到的礼物是给出的礼物序列的概率是多少?
思路:其实因为最后的序是按顺序的,所以这里隐含了一个信息,就是当k>r的时候,那么前面的序列的最大值肯定是已知序列的最小值,然后分成2段考虑。后面的已知序列除了最小值,其他的数都可以直接计算概率。对于未知序列的最大值min_x(即,已知序列的最小值,我们要计算他可能受到个数,然后算概率,最后没出现的数(即比min_x小的数)的概率可以合起来一起算);其实想起来也不复杂;
比赛的时候我的代码有2个地方被坑了!一:对于没出现的数,还算了比序列里最大的数的部分,二:我多打了一个概率和的判断,题目没有要求,然后由于是浮点数,所以我让他直接和1比较,存在误差。。。这也是我以后要注意的!
#include<cstdio> #include<cstring> #include<cmath> #include<iostream> using namespace std; const int INF = 0x3f3f3f3f; typedef long long LL; /* LL C[53][53]; void getc(int n) { int sum=1; C[n][0]=1; for(int i=1;i<=n;i++) C[n][i]=C[n][i-1]*(n-i+1)/i; }*/ __int64 fun(int a,int b) { __int64 f=1; if(a==b||b==0) return 1; b=min(b,a-b); for(int i=1;i<=b;i++,a--) { f*=a; f/=i; } // printf(" %I64d\n",f); return f; } /* double ppow(double x,int y) { double s=1; // printf("*** %d\n",y); while(y) { if(y&1) { s*=x;y--;} x*=x; y/=2; } // printf("*** %lf\n",s); return s; } */ int main() { int T,i,j; int N,k,r; double p[21]; int num[55]; // for(int i=0;i<=52;i++) // getc(i); scanf("%d",&T); while(T--) { scanf("%d%d%d",&N,&k,&r); memset(p,0,sizeof(p)); memset(num,0,sizeof(num)); double pp=0,py=0; for(i=1;i<=N;i++) { scanf("%lf",&p[i]); pp+=p[i]; } int min_x=INF,temp; for(i=1;i<=r;i++) { scanf("%d",&temp); num[temp]++; min_x=min(min_x,temp); } // if(fabs(pp-1.0)>1e-8) continue;//画蛇添足! for(i=1;i<=N;i++)//小于部分 { if(!num[i]) py+=p[i]; else break; } int kk=k; if(k==r) { for(i=N;i>0;i--) { if(num[i]!=0) { // pp*=C[kk][num[i]]*pow(p[i],num[i]); pp*=fun(kk,num[i])*pow(p[i],num[i]); kk-=num[i]; } } printf("%0.6lf\n",pp); } else if(r<k) { for(i=N;i>0;i--) { if(num[i]!=0&&i!=min_x) { // pp*=C[kk][num[i]]*pow(p[i],num[i]); pp*=fun(kk,num[i])*pow(p[i],num[i]); kk-=num[i]; } if(i==min_x) break; } double pd=0; // printf("kk= %d\n",kk); for(j=kk;j>=num[min_x];j--) { // pd+=pow(p[min_x],j)*C[kk][j]*pow(py,(kk-j)); pd+=fun(kk,j)*pow(p[min_x],j)*pow(py,(kk-j)); } printf("%0.6lf\n",pp*pd); } } return 0; } /* 20 2 3 3 0.3 0.7 1 1 2 2 3 2 0.3 0.7 1 2 3 3 2 0.3 0.2 0.5 2 3 6 8 5 0.2 0.15 0.1 0.25 0.05 0.25 3 4 4 5 5 3 3 3 0.2 0.5 0.3 1 1 1 */
用数组把组合数的值存起来会快一点,但是也差不多!
C - Floor problem
Time Limit:1000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u
Description
In this problem, we have f(n,x)=Floor[n/x]. Here Floor[x] is the biggest integer such that no larger than x. For example, Floor[1.1]=Floor[1.9]=1, Floor[2.0]=2.
You are given 3 positive integers n, L and R. Print the result of f(n,L)+f(n,L+1)+...+f(n,R), please.
Input
The first line of the input contains an integer T (T≤100), indicating the number of test cases.
Then T cases, for any case, only 3 integers n, L and R (1≤n, L, R≤10,000, L≤R).
Output
Sample Input
Sample Output
#include<stdio.h> int main() { int n,R,L; int i,j,k,T; int sum; scanf("%d",&T); while(T--) { scanf("%d%d%d",&n,&L,&R); sum=0; for(i=L;i<=R;i++) { sum+=n/i; } printf("%d\n",sum); } return 0; }
Description
Given N integers A={A[0],A[1],...,A[N-1]}. Here we have some operations:
Operation 1: AND opn L R
Here opn, L and R are integers.
For L≤i≤R, we do A[i]=A[i] AND opn (here "AND" is bitwise operation).
Operation 2: OR opn L R
Here opn, L and R are integers.
For L≤i≤R, we do A[i]=A[i] OR opn (here "OR" is bitwise operation).
Operation 3: XOR opn L R
Here opn, L and R are integers.
For L≤i≤R, we do A[i]=A[i] XOR opn (here "XOR" is bitwise operation).
Operation 4: SUM L R
We want to know the result of A[L]+A[L+1]+...+A[R].
Now can you solve this easy problem?
Input
The first line of the input contains an integer T, indicating the number of test cases. (T≤100)
Then T cases, for any case, the first line has two integers n and m (1≤n≤1,000,000, 1≤m≤100,000), indicating the number of elements in A and the number of operations.
Then one line follows n integers A[0], A[1], ..., A[n-1] (0≤A[i]<16,0≤i<n).
Then m lines, each line must be one of the 4 operations above. (0≤opn≤15)
Output
Sample Input
Sample Output
Hint
A = [1 2 4 7]
SUM 0 2, result=1+2+4=7;
XOR 5 0 0, A=[4 2 4 7];
OR 6 0 3, A=[6 6 6 7];
SUM 0 2, result=6+6+6=18.
题意:很明确,就是sum就是求区间内的和;XOR就是就是求区间内数对某数的异或,OR就是逻辑或,AND就是逻辑与,当操作时sum时候就输出值;
思路:我们可以建一棵树来模拟;
详见代码。我队友写的,,哈哈。
#include<stdio.h> struct node { int sum,XOR; }tree[4][2*1000005]; int ans[1000005]; void builde(int l,int r,int k,int i) { int m=(l+r)/2; tree[i][k].XOR=0; if(l==r) { if((1<<i)&ans[l]) tree[i][k].sum=1; else tree[i][k].sum=0; return ; } builde(l,m,k*2,i); builde(m+1,r,k*2+1,i); tree[i][k].sum=tree[i][k*2].sum+tree[i][k*2+1].sum; } void set_childe(int l,int r,int k,int i) { int flag=0,m; m=(l+r)/2; if(tree[i][k].sum==r-l+1) { flag=1; tree[i][k*2].sum=m-l+1; tree[i][k*2+1].sum=r-m; } else if(tree[i][k].sum==0) tree[i][k*2].sum=tree[i][k*2+1].sum=0,flag=1; if(tree[i][k].XOR) { if(!flag) { tree[i][k*2].sum=(m-l+1)-tree[i][k*2].sum; tree[i][k*2+1].sum=(r-m)-tree[i][k*2+1].sum; } tree[i][k*2].XOR^=1; tree[i][k*2+1].XOR^=1; } tree[i][k].XOR=0; } void update_and(int l,int r,int k,int L,int R,int i) { int m=(l+r)/2; if(L<=l&&r<=R) { tree[i][k].sum=0; return ; } set_childe(l,r,k,i); if(L<=m) update_and(l,m,k*2,L,R,i); if(m<R) update_and(m+1,r,k*2+1,L,R,i); tree[i][k].sum=tree[i][k*2].sum+tree[i][k*2+1].sum; } void update_or(int l,int r,int k,int L,int R,int i) { int m=(l+r)/2; if(L<=l&&r<=R) { tree[i][k].sum=r-l+1; return ; } set_childe(l,r,k,i); if(L<=m) update_or(l,m,k*2,L,R,i); if(m<R) update_or(m+1,r,k*2+1,L,R,i); tree[i][k].sum=tree[i][k*2].sum+tree[i][k*2+1].sum; } void update_xor(int l,int r,int k,int L,int R,int i) { int m=(l+r)/2; if(L<=l&&r<=R) { tree[i][k].sum=(r-l+1)-tree[i][k].sum; tree[i][k].XOR^=1; return ; } set_childe(l,r,k,i); if(L<=m) update_xor(l,m,k*2,L,R,i); if(m<R) update_xor(m+1,r,k*2+1,L,R,i); tree[i][k].sum=tree[i][k*2].sum+tree[i][k*2+1].sum; } int query(int l,int r,int k,int L,int R,int i) { int m=(l+r)/2; if(L<=l&&r<=R) { return tree[i][k].sum; } set_childe(l,r,k,i); int sum=0; if(L<=m) sum+=query(l,m,k*2,L,R,i); if(m<R) sum+=query(m+1,r,k*2+1,L,R,i); return sum; } int main() { int t,n,m,L,R,opn; char str[10]; scanf("%d",&t); while(t--) { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%d",&ans[i]); for(int i=0; i<4; i++) builde(1,n,1,i); while(m--) { scanf("%s",str); if(str[0]=='S') { scanf("%d%d",&L,&R); L++; R++; int sum=0,k; for(int i=0; i<4; i++) sum+=query(1,n,1,L,R,i)*(1<<i); printf("%d\n",sum); } else { scanf("%d%d%d",&opn,&L,&R); L++; R++; for(int i=0;i<4;i++) if(str[0]=='A') { if(!((1<<i)&opn)) update_and(1,n,1,L,R,i); } else if(str[0]=='O') { if((1<<i)&opn) update_or(1,n,1,L,R,i); } else if((1<<i)&opn) update_xor(1,n,1,L,R,i); } } } }
E - How many tuples
Time Limit:10000MS Memory Limit:65536KB 64bit IO Format:%I64d & %I64u
Description
Given m positive integer a[1],a[2]…a[m]. We run the following program (in C++):
const int MAXN = 20; int a[MAXN], m; int gcd(int a, int b) {return b ? gcd(b, a % b) : a;} long long cnt = 0; void gao(int cur, int g) { if (cur > m) { if (g == 1)++cnt; return; } for (int i = 1; i <= a[cur]; ++i) gao(cur + 1, g < 0 ? i : gcd(g, i)); } int main() { scanf("%d", &m); for (int i = 1; i <= m; ++i) scanf("%d", a + i); gao(1, -1); cout << cnt << endl; return 0; }
Here gcd is the Greatest Common Divisor, Obviously, the program above is to find the number of tuples (b[1], b[2], …, b[m]) such that:
(1) gcd(b[1], b[2], …, b[m])=1. (Here we define gcd(num)=num, that is: gcd(9)=9, gcd(2)=2)
(2) 1≤b[i]≤a[i]. (1≤i≤m, b[i] is an integer)
Now in this problem, the m and a[i] may be very large! So could you write one efficient program to find the answer? The answer may be too large. So you can just output the answer Mod 1,000,000,007.
Input
The first line of the input contains an integer T (T≤10,000), indicating the number of test cases.
Then T cases, for any case, only two lines.
The first line is one integer m(1≤m≤20).
The second line has m integers indicate a[1], a[2], …, a[m] (1≤a[i]≤100,000,000, 1≤i≤m).
The answer may be too large. So you can just output the answer Mod 1,000,000,007.
Output
Sample Input
Sample Output
Hint
F - Hua Rong Dao
Time Limit:1000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u
Description
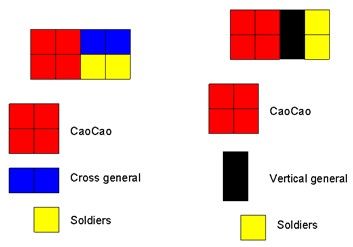
Cao Cao was hunted down by thousands of enemy soldiers when he escaped from Hua Rong Dao. Assuming Hua Rong Dao is a narrow aisle (one N*4 rectangle), while Cao Cao can be regarded as one 2*2 grid. Cross general can be regarded as one 1*2 grid.Vertical general can be regarded as one 2*1 grid. Soldiers can be regarded as one 1*1 grid. Now Hua Rong Dao is full of people, no grid is empty.
There is only one Cao Cao. The number of Cross general, vertical general, and soldier is not fixed. How many ways can all the people stand?
Input
There is a single integer T (T≤4) in the first line of the test data indicating that there are T test cases.
Then for each case, only one integer N (1≤N≤4) in a single line indicates the length of Hua Rong Dao.
Output
Sample Input
Sample Output
Hint
Here are 2 possible ways for the Hua Rong Dao 2*4.
题意:华容道,这个游戏应该不陌生吧,是的这题就是让你求可能的组成情况,当然曹操是必须在的,哈哈
思路:dfs,记录曹操的位置在左下角,然后搜素,大神队友做的。。。哈哈。
#include <stdio.h> #include <string.h> #include <algorithm> using namespace std; int d[4][2] = { {0, 0}, {0, 1}, {1, 0}, {1, 1} }; int dir[3][3][2] = { { {0, 1}, {0, 0} }, { {1, 0}, {0, 0} }, { {0, 0} } }; int cnt[3] = {2, 2, 1}; int r, v[5][5], tmp; const int c = 4; bool ok(int k, int x, int y) { for (int i = 0; i< cnt[k]; i++) { int p = x + dir[k][i][0], q = y + dir[k][i][1]; if (p<= 0 || p >r) return false; if (q<= 0 || q >c) return false; if (v[p][q]) return false; } return true; } void clear(int k, int x, int y, int t) { for (int i = 0; i< cnt[k]; i++) { int p = x + dir[k][i][0], q = y + dir[k][i][1]; v[p][q] = t; } } void dfs(int x, int y) { if (y >c) x = x + 1, y = 1; if (x == r + 1) { tmp++; return; } if (v[x][y]) dfs(x, y + 1); for (int i = 0; i< 3; i++) { if (ok(i, x, y)) { clear(i, x, y, 1); dfs(x, y + 1); clear(i, x, y, 0); } } } int find(int x, int y) { memset(v, 0, sizeof(v)); for (int i = 0; i< 4; i++) v[x + d[i][0]][y + d[i][1]] = 1; tmp = 0; dfs(1, 1); return tmp; } int solve() { int ans = 0; for (int i = 1; i< r; i++) { for (int j = 1; j< c; j++) { ans += find(i, j); } } return ans; } int main () { int t[10]; for (r = 1; r<= 4; r++) { t[r] = solve(); } int cas, n; scanf("%d", &cas); while (cas--) { scanf("%d", &n); printf("%d\n", t[n]); } return 0; }
G - Mod problem
Time Limit:1000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u
Description
Given one non-negative integer A and one positive integer B, it’s very easy for us to calculate A Mod B. Here A Mod B means the remainder of the answer after A is divided by B. For example, 7 Mod 5 = 2, 12 Mod 3 = 0, 0 Mod 3 = 0.
In this problem, we use the following rules to express A.
(1) One non-empty string that only contains {0,1,2,3,4,5,6,7,8,9} is valid.
For example, 123, 000213, 99213. (Leading zeros is OK in this problem)
(2) If w is valid, then [w]x if valid. Here x is one integer that 0<x<10.
For example, [012]2=012012, [35]3[7]1=3535357.
(3) If w and v are valid, then wv is valid.
For example, w=[231]2 and v=1, then wv=[231]21 is valid (which is 2312311).
Now you are given A and B. Here A is express as the rules above and B is simply one integer, you are expected to output the A Mod B.
Input
The first line of the input contains an integer T(T≤10), indicating the number of test cases.
Then T cases, for any case, only two lines.
The first line is one non-empty and valid string that expresses A, the length of the string is no more than 1,000.
The second line is one integer B(0<B<2,000,000,000).
You may assume that the length of number A in decimal notation will less than 2^63.
Output
Sample Input
Sample Output
#include <stdio.h> #include <string.h> #include <algorithm> using namespace std; #define ll __int64 struct node { ll val,len; }; char str[1005]; int t,mod; ll qmod(ll a,ll b) { ll s = 1; while(b) { if(b&1) s = (s*a)%mod; a = (a*a)%mod; b>>=1; } return s%mod; } node dfs(int l,int r) { int i,j,top = 0; int left,right,k,cnt; node ans; ans.val = 0; ans.len = 0; for(i = l; i<=r; i++) { if(str[i]=='[') { if(!top) left=i+1; ++top; } else if(str[i]==']') { --top; if(!top) { right = i-1; i++; cnt = str[i]-'0'; node tem=dfs(left,right); ll base = qmod(10,tem.len); ans.len+=cnt*tem.len; ans.val=(ans.val*qmod(base,cnt))%mod; ll s=1,bb=base; while(--cnt) { s+=bb; bb=(bb*base)%mod; s%=mod; } tem.val=(tem.val*s)%mod; ans.val = (ans.val+tem.val)%mod; } } else if(!top) { ans.val=ans.val*10+str[i]-'0'; ans.val%=mod; ans.len++; } } return ans; } int main() { scanf("%d",&t); while(t--) { scanf("%s%d",str,&mod); node ans = dfs(0,strlen(str)-1); printf("%I64d\n",ans.val); } return 0; }
Description
One integer number x is called "Mountain Number" if:
(1) x>0 and x is an integer;
(2) Assume x=a[0]a[1]...a[len-2]a[len-1](0≤a[i]≤9, a[0] is positive). Any a[2i+1] is larger or equal to a[2i] and a[2i+2](if exists).
For example, 111, 132, 893, 7 are "Mountain Number" while 123, 10, 76889 are not "Mountain Number".
Now you are given L and R, how many "Mountain Number" can be found between L and R (inclusive) ?
Input
The first line of the input contains an integer T (T≤100), indicating the number of test cases.
Then T cases, for any case, only two integers L and R (1≤L≤R≤1,000,000,000).
Output
Sample Input
Sample Output
做法:。。。。数位dp。
大神队友做的,我是初学者,,,,不要介意。
#include <stdio.h> #include <string.h> #include <algorithm> using namespace std; int t; int bit[20],len,l,r; int dp[20][10][2]; int dfs(int pos,int pre,int odd,int zero,int doing) { if(pos==-1) return 1; if(dp[pos][pre][odd]!=-1 && !doing) return dp[pos][pre][odd]; int end = doing?bit[pos]:9; int ans = 0; for(int i = 0; i<=end; i++) { if(!(i||zero)) ans+=dfs(pos-1,9,0,zero||i,doing&&i==end); else if(odd && pre<=i) ans+=dfs(pos-1,i,!odd,zero||i,doing&&i==end); else if(!odd && pre>=i) ans+=dfs(pos-1,i,!odd,zero||i,doing&&i==end); } if(!doing) dp[pos][pre][odd] = ans; return ans; } int cal(int x) { len = 0; while(x) { bit[len++] = x%10; x/=10; } return dfs(len-1,9,0,0,1); } int main() { scanf("%d",&t); while(t--) { memset(dp,-1,sizeof(dp)); scanf("%d%d",&l,&r); printf("%d\n",cal(r)-cal(l-1)); } return 0; }
I - Star
Time Limit:1000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u
Description
Input
The first line of the input contains an integer T (T≤10), indicating the number of test cases.
For each test case:
The first line contains one integer n (1≤n≤100), the number of stars.
The next n lines each contains two integers x and y (0≤|x|, |y|≤1,000,000) indicate the points, all the points are distinct.
Output
Sample Input
Sample Output
#include <stdio.h> #include <string.h> #include <math.h> #include <algorithm> using namespace std; struct node { double x,y; }a[105]; int main() { int t,i,j,n,k,cnt; scanf("%d",&t); while(t--) { cnt = 0; scanf("%d",&n); for(i = 0;i<n;i++) scanf("%lf%lf",&a[i].x,&a[i].y); for(i = 0;i<n-2;i++) { for(j = i+1;j<n-1;j++) { for(k = j+1;k<n;k++) { double x = sqrt((a[i].x-a[j].x)*(a[i].x-a[j].x)+(a[i].y-a[j].y)*(a[i].y-a[j].y)); double y = sqrt((a[i].x-a[k].x)*(a[i].x-a[k].x)+(a[i].y-a[k].y)*(a[i].y-a[k].y)); double z = sqrt((a[k].x-a[j].x)*(a[k].x-a[j].x)+(a[k].y-a[j].y)*(a[k].y-a[j].y)); if(x*x+y*y>z*z && x*x+z*z>y*y && y*y+z*z>x*x) cnt++; } } } printf("%d\n",cnt); } return 0; }
Description
Now you are given one non-negative integer n in 10-base notation, it will only contain digits ('0'-'9'). You are allowed to choose 2 integers i and j, such that: i!=j, 1≤i<j≤|n|, here |n| means the length of n’s 10-base notation. Then we can swap n[i] and n[j].
For example, n=9012, we choose i=1, j=3, then we swap n[1] and n[3], then we get 1092, which is smaller than the original n.
Now you are allowed to operate at most M times, so what is the smallest number you can get after the operation(s)?
Please note that in this problem, leading zero is not allowed!
Input
The first line of the input contains an integer T (T≤100), indicating the number of test cases.
Then T cases, for any case, only 2 integers n and M (0≤n<10^1000, 0≤M≤100) in a single line.
Output
Sample Input
Sample Output
#include <stdio.h> #include <string.h> #include <algorithm> using namespace std; int t,n,minn; char str[1005]; int main() { int i,j; scanf("%d",&t); while(t--) { scanf("%s%d",str,&n); if(!n) { printf("%s\n",str); continue; } int len = strlen(str),flag = -1; minn = str[0]; for(i = 1; i<len; i++) { if(str[i]<minn && str[i]!='0') { minn = str[i]; flag = i; } } if(flag!=-1) { swap(str[flag],str[0]); n--; } for(i = 1; i<len; i++) { if(!n) break; minn = str[i]; flag = -1; for(j = len-1; j>i; j--) { if(str[j]<minn) { flag = j; minn = str[j]; } } if(flag!=-1) { swap(str[flag],str[i]); n--; } } printf("%s\n",str); } return 0; }
K - Tickets
Time Limit:3000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u
Description
You have won a collection of tickets on luxury cruisers. Each ticket can be used only once, but can be used in either direction between the 2 different cities printed on the ticket. Your prize gives you free airfare to any city to start your cruising, and free airfare back home from wherever you finish your cruising.
You love to sail and don't want to waste any of your free tickets. How many additional tickets would you have to buy so that your cruise can use all of your tickets?
Now giving the free tickets you have won. Please compute the smallest number of additional tickets that can be purchased to allow you to use all of your free tickets.
Input
There is one integer T (T≤100) in the first line of the input.
Then T cases, for any case, the first line contains 2 integers n, m (1≤n, m≤100,000). n indicates the identifier of the cities are between 1 and n, inclusive. m indicates the tickets you have won.
Then following m lines, each line contains two integers u and v (1≤u, v≤n), indicates the 2 cities printed on your tickets, respectively.
Output
Sample Input
Sample Output
#include<stdio.h> #include<string.h> const int N = 100005; int edgN,fath[N]; int findObj(int x) { if(x!=fath[x]) fath[x]=findObj(fath[x]); return fath[x]; } void setNode(int u,int v) { u=findObj(u); v=findObj(v); if(u!=v) { edgN--; fath[u]=v; } } int main() { int t,linkEdgN[N],ans,n,m,u,v; scanf("%d",&t); while(t--) { scanf("%d%d",&n,&m); for(int i=0;i<=n; i++) { fath[i]=i; linkEdgN[i]=0; } edgN=0; ans=0; while(m--) { scanf("%d%d",&u,&v); if(linkEdgN[u]==0) edgN++; if(linkEdgN[v]==0) edgN++; setNode(u,v); linkEdgN[u]++; linkEdgN[v]++; if(linkEdgN[u]&1)ans++; else ans--; if(linkEdgN[v]&1)ans++; else ans--; } edgN--; ans-=(edgN+1)*2; ans/=2; if(ans<0) printf("%d\n",edgN); else printf("%d\n",edgN+ans); } }
http://acm.hust.edu.cn/vjudge/contest/view.action?cid=65448#overview
终于写完了。。。。。。。还有一题,坐等大神队友来AK。。。哈哈。