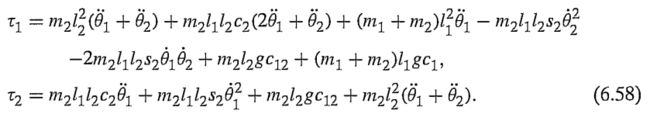1、牛顿-欧拉法
牛顿欧拉法分两步,首先向外迭代,计算出各个杆的角速度,角加速度,质心线加速度,进而计算出每个连杆的合外力(矩);再向内迭代,计算出每个连杆的内力,进而得到关节力矩。迭代过程如下:
2、Matlab代码
由于牛顿-欧拉法迭代的特性,使其对于编程来说比较方便实现。基于算法,笔者编写了Matlab函数NewtonEulerDynamics用于求解各个关节力矩的解析表达式:
function torque_list = NewtonEulerDynamics(dh_list, mass_list, mass_center_list, inertia_tensor_list, f_external)
% 输入参数:
% dh_list:机器人DH参数
% mass_list: 连杆的质量,单位kg
% mass_center_list:连杆质心在连杆坐标系下的位置,单位:m
% inertia_tensor_list:连杆关于质心坐标系的惯性张量,质心坐标系与连杆坐标系方位一致
% f_external:施加在末端连杆的外力和外力矩
% 输出参数:
% torque_list:用q,dq,ddq(关节位置、速度、加速度)表达的关节力矩
[rows, columns] = size(dh_list);
number_of_links = rows - 1;
if columns ~= 4
error('wrong DH parameters!')
end
T = sym([]);
R = sym([]);
a = sym([]);
d = sym([]);
alpha = sym([]);
theta = sym([]);
for i = 1:rows
% 定义关节位置,速度,加速度符号
eval(['syms ','q',num2str(i),' real;']);
eval(['syms ','dq',num2str(i),' real;']);
eval(['syms ','ddq',num2str(i),' real;']);
eval(['q(i)=','q',num2str(i),';']);
eval(['dq(i)=','dq',num2str(i),';']);
eval(['ddq(i)=','ddq',num2str(i),';']);
end
for i = 1:rows
dh = dh_list(i,:);
alpha(i) = dh(1);
a(i) = dh(2);
d(i) = dh(3);
theta(i) = dh(4);
if i == rows
q(i) = 0;
end
T(:,:,i) = [cos(q(i)), -sin(q(i)), 0, a(i);
sin(q(i))*cos(alpha(i)), cos(q(i))*cos(alpha(i)), -sin(alpha(i)), -sin(alpha(i))*d(i);
sin(q(i))*sin(alpha(i)), cos(q(i))*sin(alpha(i)), cos(alpha(i)), cos(alpha(i))*d(i);
0, 0, 0, 1];
T = T(:,:,i);
% 提取旋转矩阵并求逆
R(:,:,i) = simplify(inv(T(1:3,1:3)));
P(:,:,i) = T(1:3,4:4);
end
% 关节轴
z = [0,0,1]';
% 重力加速度符号
syms g real
% 外推 --->
for i = 0:number_of_links-1
if i == 0
wi = [0,0,0]';
dwi = [0,0,0]';
dvi = [0, g, 0]';
else
wi = w(:,i);
dwi = dw(:,i);
dvi = dv(:,i);
end
w(:,:,i+1) = R(:,:,i+1)*wi + dq(i+1)*z;
dw(:,:,i+1) = R(:,:,i+1)*dwi + cross(R(:,:,i+1)*wi,dq(i+1)*z) + ddq(i+1)*z;
dv(:,:,i+1) = R(:,:,i+1)*(cross(dwi,P(:,:,i+1)) + cross(wi,cross(wi,P(:,:,i+1))) + dvi);
dvc(:,:,i+1) = cross(dw(:,:,i+1),mass_center_list(i+1,:)')...
+ cross(w(:,:,i+1),cross(w(:,:,i+1),mass_center_list(i+1,:)'))...
+ dv(:,:,i+1);
F(:,:,i+1) = mass_list(i+1)*dvc(:,:,i+1);
N(:,:,i+1) = inertia_tensor_list(:,:,i+1)*dw(:,:,i+1) + cross(w(:,:,i+1),inertia_tensor_list(:,:,i+1)*w(:,:,i+1));
end
f = sym([]);
n = sym([]);
% 内推 <---
for i = number_of_links:-1:1
if i == number_of_links
f(:,:,i+1) = f_external(1,:)';
n(:,:,i+1) = f_external(2,:)';
end
f(:,:,i) = R(:,:,i+1)\f(:,:,i+1) + F(:,:,i);
f(:,:,i) = simplify(f(:,:,i));
n(:,:,i) = N(:,:,i) + R(:,:,i+1)\n(:,:,i+1) + cross(mass_center_list(i,:)',F(:,:,i))...
+ cross(P(:,:,i+1),R(:,:,i+1)\f(:,:,i+1));
n(:,:,i) = simplify(n(:,:,i));
torque_list(i) = dot(n(:,:,i),z);
end
torque_list = torque_list';
以上代码适用于修改的DH模型,如果是标准的DH模型需要做一点修改。代码运行后将给出各个关节扭矩的封闭解。
下面的代码给出一个用例:
clc;
clear;
syms q1 q2 m1 m2 L1 L2 real
dh_params = [0, 0, 0, q1;
0, L1, 0, q2;
0, L2, 0, 0];
mass_center = [L1, 0, 0;
L2, 0, 0;];
mass = [m1,m2];
inertia_1 = [0,0,0;
0,0,0;
0,0,0];
inertia_2 = [0,0,0;
0,0,0;
0,0,0];
inertia_tensor(:,:,1) = inertia_1;
inertia_tensor(:,:,2) = inertia_2;
f_ext = [0,0,0;
0,0,0];
torque = NewtonEulerDynamics(dh_params, mass, mass_center, inertia_tensor, f_ext);
注意dh_params 第三行给出的是末端执行器相对于最后一根连杆的坐标表达。上述代码求解的问题是书中的例题6.7,求解平面二连杆的动力学方程:
运行后输出:
torque =
L1^2*ddq1*m1 + L1^2*ddq1*m2 + L2^2*ddq1*m2 + L2^2*ddq2*m2 + L2*g*m2*cos(q1 + q2) + L1*g*m1*cos(q1) + L1*g*m2*cos(q1) - L1*L2*dq2^2*m2*sin(q2) + 2*L1*L2*ddq1*m2*cos(q2) + L1*L2*ddq2*m2*cos(q2) - 2*L1*L2*dq1*dq2*m2*sin(q2)
L2*m2*(cos(q2)*(L1*ddq1 + g*cos(q1)) + sin(q2)*(L1*dq1^2 - g*sin(q1)) + L2*(ddq1 + ddq2))
书中的求解结果:
对比可以表明两者一致,证明计算是正确的。当然,编写的代码本身对于关节数目是没有限制的,可用于更多关节机器人的动力学方程计算。