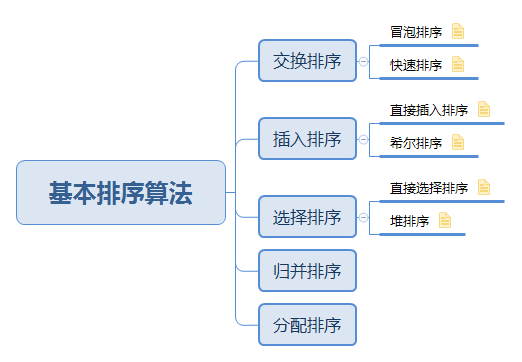
基本算法分类结构
参考链接
http://www.cnblogs.com/0201zcr/p/4764427.html
http://www.cnblogs.com/qqzy168/archive/2013/08/03/3219201.html
交换排序—冒泡排序
描述:
在排序数组Arrys中,对当前还未排好顺序的全部输,自上而下对相邻两数进行比较和调整。让较大的数往下沉,较小往下沉。即:发现相邻比较数顺序不符合排序要求,交换位置。
步骤:
比较相邻的元素。如果第一个比第二个大,就交换他们两个。
1.遍历数组起始位i,i到arrys.length-1
2.再次遍历数组,j位置到arrys.length-1-i
3.条件判断,交换位置操作
/**
* 冒泡升序
* 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
* 针对所有的元素重复以上的步骤,除了最后一个。
* 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
* @param arrys
* @return
*/
public Integer[] bubbleSortByAsc(Integer[] arrys){
Integer[] clone = arrys.clone();
for(int i=0;iclone[j+1]){
int temp=clone[j];
clone[j]=clone[j+1];
clone[j+1]=temp;
}
}
}
return clone;
}
/**
* 冒泡降序
* @param arrys
* @return
*/
public Integer[] bubbleSortByDesc(Integer[] arrys){
Integer[] clone = arrys.clone();
for(int i=0;iclone[j+1]){
int temp=clone[j];
clone[j]=clone[j+1];
clone[j+1]=temp;
}
}
}
return clone;
}
交换排序—快速排序
描述:
选择一个基准元素,通常以第一个或最后一个,通过一趟排序,将待排序列分成两部分。一部分比基准元素小,另一部分比基准元素大或相等
/**
* 快速排序升序
*
* @param nums src
* @return result
*/
public Integer[] quickSortByAsc(Integer[] nums) {
Integer[] clone = nums.clone();
System.out.println("quick sort by Asc");
quickSortByAsc(clone, 0, clone.length - 1);
return clone;
}
public void quickSortByAsc(Integer[] nums, int low, int high) {
if (low < high) {
int middle = getMiddleAsc(nums, low, high);
quickSortByAsc(nums, low, middle - 1);
quickSortByAsc(nums, middle + 1, high);
}
}
/**
* 获取中轴位置(Asc升序)
*
* @param nums src
* @param low low
* @param high high
* @return position
*/
private int getMiddleAsc(Integer[] nums, int low, int high) {
int middleNum = nums[low];//取第一次传入的low位位中轴数
while (low < high) {
while (low < high && nums[high] >= middleNum) {//右边high游标不断前移,如果当前位置的数大于中轴上的数
high--;
}
nums[low] = nums[high];//小的移到左边
while (low < high && nums[low] <= middleNum) {//左边low游标不断后移,如果当前low位置的数小于中轴上的数
low++;
}
nums[high] = nums[low];//大的移到右边
}
nums[low] = middleNum;//将中轴数放到正确的位置上
return low;
}
/**
* 快速排序降序
*
* @param nums src
* @return result
*/
public Integer[] quickSortByDesc(Integer[] nums) {
Integer[] clone = nums.clone();
System.out.println("quick sort by desc:");
quickSortByDesc(clone, 0, clone.length - 1);
return clone;
}
private void quickSortByDesc(Integer[] nums, int low, int high) {
if (low < high) {
int middle = getMiddleDesc(nums, low, high);
quickSortByDesc(nums, low, middle - 1);//对中轴左边继续排序
quickSortByDesc(nums, middle + 1, high);//对中轴右边继续排序
}
}
/**
* 获取中轴位置(Desc降序)
*
* @param nums src
* @param low low
* @param high high
* @return position
*/
private int getMiddleDesc(Integer[] nums, int low, int high) {
int middleNum = nums[low];//取第一次传入的low位位中轴数
while (low < high) {
while (low < high && nums[high] <= middleNum) {//右边high游标不断前移,如果当前位置的数小于中轴上的数
high--;
}
nums[low] = nums[high];//大的数移到左边
while (low < high && nums[low] >= middleNum) {//左边low游标不断后移,如果当前low位置的数大于中轴上的数
low++;
}
nums[high] = nums[low];//小的数移到右边
}
nums[low] = middleNum;//将中轴数放到正确的位置上
return low;
}
插入排序——直接插入排序
描述:
在排序的数组中,假设前面n-1(n>=2)个数已经排好顺序,现在将第n个数插入到前面的有序数组中,使得这n个数也是排好顺序。反复循环。直到排列完成。
/**
* 基本思想:每步将一个待排序的记录,按其顺序码大小插入到
* 前面已经排序的字序列的合适位置(从后向前找到合适位置后),
* 直到全部插入排序完为止。
*
* 从第一个元素开始,该元素可以认为已经被排序
* 取出下一个元素,在已经排序的元素序列中从后向前扫描
* 如果该元素(已排序)大于新元素,将该元素移到下一位置
* 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
* 将新元素插入到该位置中
* 重复步骤2
* @param nums
*/
public Integer[] insertSortByAsc(Integer[] nums){
System.out.println("insert sort by Asc:");
Integer[] clone = nums.clone();
for(int i=0;i0&&temp0&&temp>clone[j-1];j--){//满足待排序数大于前面的数条件,j--
clone[j]=clone[j-1];//整体后移一位
}
clone[j]=temp;
}
return clone;
}
插入排序——希尔排序
描述:将要排序的一组数按某个增量 d(n/2,n为要排序数的个数)分成若干组,每组中记录的下标相差 d.对每组中全部元素进行直接插入排序,然后再用一个较小的增量(d/2)对它进行分组,在每组中再进行直接插入排序。当增量减到 1 时,进行直接插入排序后,排序完成。
/**
* 希尔排序升序
* 基本思想:
* 将数组拆分成d长度的小数组,最开始d长度为length/2
* 对小数组插入排序
* 再将d长度缩小为d/2
* 重复操作,直到d=1
* @param nums src numbers
* @return result numbers
*/
public Integer[] shellSortAsc(Integer[] nums) {
System.out.println("shell sort by Asc:");
Integer[] clone = nums.clone();
for (int d = clone.length / 2; d >= 1; d /= 2) {//d每次缩小二分之一
for (int groupStarPosition = 0; groupStarPosition <= clone.length - d; groupStarPosition ++) {//分成d长度的段
//对d长度的每组数进行插入排序,每组起始坐标为groupStarPosition
for (int j = groupStarPosition; j < groupStarPosition+d; j++) {
int temp = clone[j];
int k = 0;
for (k = j; k > groupStarPosition && temp < clone[k - 1]; k--) {
clone[k] = clone[k - 1];
}
clone[k] = temp;
}
}
}
return clone;
}
/**
* 希尔排序升序
* 基本思想:
* 将数组拆分成d长度的小数组,最开始d长度为length/2
* 对小数组插入排序
* 再将d长度缩小为d/2
* 重复操作,直到d=1
* @param nums src numbers
* @return result numbers
*/
public Integer[] shellSortByDesc(Integer[] nums) {
System.out.println("shell sort by Desc:");
Integer[] clone = nums.clone();
for (int d = clone.length / 2; d >= 1; d /= 2) {//d每次缩小二分之一
for (int groupStarPosition = 0; groupStarPosition <= clone.length - d; groupStarPosition ++) {//分成d长度的段
//对d长度的每组数进行插入排序,每组起始坐标为groupStarPosition
for (int j = groupStarPosition; j < groupStarPosition+d; j++) {
int temp = clone[j];
int k = 0;
for (k = j; k > groupStarPosition && temp > clone[k - 1]; k--) {
clone[k] = clone[k - 1];
}
clone[k] = temp;
}
}
}
return clone;
}
选择排序——直接选择排序
描述:排序的一组数中,选出最小的一个数与第一个位置的数交换;
然后在剩下的数当中再找最小的与第二个位置的数交换,如此循环到倒数第二个数和最后一个数比较为止。
/**
* 选择排序(升序)
* 每次选择一个最小值排在有序数组的后面一位上
* 主要关心每次选择的最小值的位置与值,再将此位置与数值交换
*
* @param nums src numbers
* @return result numbers
*/
public Integer[] selectSortByAsc(Integer[] nums) {
System.out.println("select sort by Asc:");
Integer[] clone = nums.clone();
int position = 0;//记录本次选择数的数组位置
int value = 0;//记录本次选择的值
for (int i = 0; i < clone.length; i++) {
value = clone[i];//初始值为clone[i]
for (int j = i; j < clone.length; j++) {
//如果发现有值比当前选择的值小,position记录他在数组中的位置,更新value的值,进行下次比较
if (clone[j] <= value) {
position = j;
value = clone[j];
}
}
//将此次选择的最小值与clone[i]位置交换
int temp = clone[i];
clone[i] = value;
clone[position] = temp;
}
return clone;
}
/**
* 选择排序(降序)
* 每次选择一个最大值排在有序数组的后面一位上
* 主要关心每次选择的最大值的位置与值,再将此位置与起始选择位置交换
*
* @param nums src numbers
* @return result numbers
*/
public Integer[] selectSortByDesc(Integer[] nums) {
System.out.println("select sort by Desc:");
Integer[] clone = nums.clone();
int position = 0;//记录本次选择数的数组位置
int value = 0;//记录本次选择的值
for (int i = 0; i < clone.length; i++) {
value = clone[i];//初始值为clone[i]
for (int j = i; j < clone.length; j++) {
//如果发现有值比当前选择的值大,position记录他在数组中的位置,更新value的值,进行下次比较
if (clone[j] >= value) {
position = j;
value = clone[j];
}
}
//将此次选择的最小值与clone[i]位置交换
int temp = clone[i];
clone[i] = value;
clone[position] = temp;
}
return clone;
}
选择排序——堆排序(待续)
归并排序
归并(Merge)排序法是将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。
/**
* 归并排序升序
*
* @param nums src numbers
* @return result numbers
*/
public Integer[] mergeSortAsc(Integer[] nums) {
System.out.println("merge sort By Asc:");
Integer[] clone = nums.clone();
mergeSortAsc(clone, 0, clone.length - 1);
return clone;
}
/**
* low 到high 元素归并
*
* @param nums src numbers
* @param low 归并元素起始位置
* @param high 归并元素结束位置
*/
public void mergeSortAsc(Integer[] nums, int low, int high) {
if (low < high) {
int middle = (low + high) / 2;
mergeSortAsc(nums, low, middle);//对左边归并排序
mergeSortAsc(nums, middle + 1, high);//对右边归并排序
mergeAsc(nums, low, middle, high);//归并
}
}
/**
* 归并操作,将有序的两边的子序列合并成整体有序的数
*
* @param nums 待排序数组
* @param low 待排的开始位置
* @param middle 待排中间位置
* @param high 待排结束位置
*/
public void mergeAsc(Integer[] nums, int low, int middle, int high) {
//辅助数组,用于存储新排序好的数组
Integer[] temp = new Integer[high - low + 1];
//左指针
int left = low;
//右指针
int right = middle + 1;
//辅助数组的标记
int k = 0;
// 把较小的数先移到新数组中
while (left <= middle && right <= high) {
if (nums[left] < nums[right]) {
temp[k] = nums[left];
left++;
k++;
} else {
temp[k] = nums[right];
right++;
k++;
}
}
// 把左边剩余的数移入数组
while (left <= middle) {
temp[k++] = nums[left++];
}
// 把右边剩余的数移入数组
while (right <= high) {
temp[k++] = nums[right++];
}
// 把新数组中的数覆盖回到nums数组
for (int i = 0; i < temp.length; i++) {
nums[low + i] = temp[i];
}
}
/**
* 归并排序(降序)
*
* @param nums src numbers
* @return result numbers
*/
public Integer[] mergeSortDesc(Integer[] nums) {
System.out.println("merge sort by Desc:");
Integer[] clone = nums.clone();
mergeSortDesc(clone, 0, clone.length - 1);
return clone;
}
/**
* low 到high 元素desc归并
*
* @param nums src numbers
* @param low 归并元素起始位置
* @param high 归并元素结束位置
*/
public void mergeSortDesc(Integer[] nums, int low, int high) {
if (low < high) {
int middle = (low + high) / 2;
mergeSortDesc(nums, low, middle);
mergeSortDesc(nums, middle + 1, high);
mergeDesc(nums, low, middle, high);
}
}
/**
* 归并操作,将有序的两边的子序列合并成整体有序的数
*
* @param nums 待排序数组
* @param low 待排的开始位置
* @param middle 待排中间位置
* @param high 待排结束位置
*/
public void mergeDesc(Integer[] nums, int low, int middle, int high) {
//辅助数组,用于存储新排序好的数组
Integer[] temp = new Integer[high - low + 1];
//左指针
int left = low;
//右指针
int right = middle + 1;
//辅助数组的标记
int k = 0;
// 把较大的数先移到新数组中
while (left <= middle && right <= high) {
if (nums[left] > nums[right]) {
temp[k] = nums[left];
left++;
k++;
} else {
temp[k] = nums[right];
right++;
k++;
}
}
// 把左边剩余的数移入数组
while (left <= middle) {
temp[k++] = nums[left++];
}
// 把右边剩余的数移入数组
while (right <= high) {
temp[k++] = nums[right++];
}
// 把新数组中的数覆盖回到nums数组
for (int i = 0; i < temp.length; i++) {
nums[low + i] = temp[i];
}
}