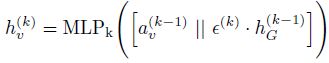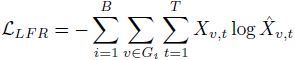摘要:本文提出一种基于局部特征保留的图卷积网络架构,与最新的对比算法相比,该方法在多个数据集上的图分类性能得到大幅度提升,泛化性能也得到了改善。
本文分享自华为云社区《论文解读:基于局部特征保留的图卷积神经网络架构(LPD-GCN)》,原文作者:PG13 。
近些年,很多研究者开发了许多基于图卷积网络的方法用于图级表示学习和分类应用。但是,当前的图卷积网络方法无法有效地保留图的局部信息,这对于图分类任务尤其严重,因为图分类目标是根据其学习的图级表示来区分不同的图结构。为了解决该问题,这篇文章提出了一种基于局部特征保留的图卷积网络架构[1]。与最新的对比算法相比,该方法在多个数据集上的图分类性能得到大幅度提升,泛化性能也得到了改善。
1、引言
图(网络)结构数据可以通过图中的节点和连接节点之间的边进行建模来捕获实体和实体之间的丰富信息。图结构数据已经在诸多研究领域得到了广泛的应用,包括生物学(蛋白质与蛋白质的相互作用网络)、化学(分子结构/化合物结构)、社会科学(社交网络/文献引用网络)和许多其他的研究领域。图结构数据不仅能够对结构化信息进行高效存储,而且在现代机器学习任务中也扮演着极其重要的角色。在诸多的机器学习任务中,图分类是近几年来广泛研究的一项重要任务。图分类的目的是将给定的图划分到特定的类别。例如,为了区分化学中有机分子的各种图结构,需要对其推断并聚合整个图拓扑结构(在分子网络中拓扑结构由单个原子及其直接键组成)以及节点特征(例如原子属性),并使用推断和聚合的信息来预测图的类别。
近年来,国际上发表了很多旨在解决图分类问题的技术。一种传统且流行的技术是设计一个图核函数来计算图与图之间的相似度,然后输入到基于核函数的分类器(如SVM)来进行图分类任务。尽管基于图核的方法是有效的,但存在计算瓶颈,而且其特征选择的过程与后续分类过程是分开的。为了解决上述挑战,端到端的图神经网络方法受到了越来越多的研究关注。而其中,图卷积神经网络(GCNs)又是解决图分类问题的最热门的一类图神经网络方法。
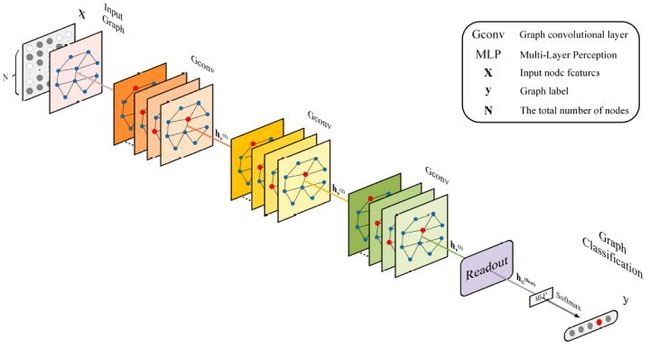
目前的图卷积神经网络大致遵循消息传递(Message Passing Neural Network,MPNN)框架[2]。该框架由消息传递阶段和读出阶段两部分组成,其中消息传递阶段是通过聚集节点的邻域特征来更新每个节点的特征向量,而读出阶段是通过全局的池化模块来生成整个图级的特征。图卷积神经网络使用消息传递功能来迭代地运行图卷积操作,使得特征信息能够传播很长的距离,从而可以学习不同范围的邻域特征。在经过k次的图卷积操作后,可以提取有用的节点或者边的特征来解决许多基于节点和边的分析任务(例如,节点分类,链路预测等)。为了解决图级的任务(例如图分类),读出模块需要聚合全体的节点或局部结构的信息来生成图级表示。下图给出了用于图分类任务的图卷积神经网络的通用框架。在现有的消息传递框架基础下,很多的研究者已经开发出了具有各种消息传递函数,节点更新函数和读出模块的许多图卷积神经网络的变体。
但是,现有的基于图卷积神经网络方法的主要局限性在于,用于图级表示学习的图卷积神经网络方法缺乏对局部特征信息的有效利用。换句话说,它们过分强调区分不同图结构的能力,而忽略了节点的局部表达能力,从而容易导致过度平滑的问题(每个节点的特征表示趋于一致),特别是当加深神经网络的层数时,过平滑问题会愈趋严重。这是因为在局部邻域聚合过程中没有对邻域的特征信息进行有效地区分和辨别,使得学到的节点特征的局部表达能力不强,再加上过平滑的影响,从而大大限制了全局的图级特征的表示能力。
众所周知,图级表示是通过聚集节点的局部特征而得到的,因此如何在优化的过程中保持局部表达能力是提高图表示能力的关键前提。针对图级表示学习目标,现有的用于保持特征局部表达能力的研究方法可以大致分为三个派系:(1)设计不同的图卷积操作和读出操作,(2)设计分层聚类方法,(3)探索新的模型架构。在第一个派系中,Xu等人发现基于现有消息传递框架下的方法学习到的图级别表示并不能有效地区分不同的图结构,并且他们提出了一个图同构网络模型(GIN)[3]。图同构网络采用了一种单射聚合更新方法将不同的节点邻居映射到不同的特征向量。这样就能保留图的局部结构和节点特征,使得图神经网络和Weisfeiler-Lehman测试一样有效。Fan等人提出了一种类似于图注意力网络(GATs)[4]的结构化自注意力架构,用于图级表示学习,其中以节点为中心的注意力机制将具有可学习权重的不同邻居节点特征聚合在一起,并将层级注意力机制和图级注意力机制作为模型的读出模块,可将来自不同节点、不同深度的重要特征聚合到模型的输出中。在第二个派系中,也就是在层次聚类方法中,许多研究工作证明图除了节点或图级结构之间的二分法外,还显示出其它丰富的层次结构。比如最近的一项前沿工作提出了DIFFPOOL[5],这是一种能够与图卷积联合训练的可微分层次化池化方法,可以用于提炼局部特征信息。
总而言之,上述两类用于图分类任务的方法能够很好地拟合大多数训练数据集,但是其泛化能力非常有限,在测试集上的效果表现平平,难以突破现有方法的瓶颈。而在第三类派系中,也就是研究新的模型架构,一些研究人员试图解决在训练图卷积神经网络的存在的实际困难或者过度平滑问题。例如,Xu等人[6]提出了一种跳跃知识网络(JK-Net)架构,以将网络的最后的图卷积层与所有先前的隐藏层连接起来,也就是类似于残差网络的结构。通过这样的设计,使得模型最后的层可以有选择性地利用来自前面不同层的邻域信息,从而可以在固定数量的图卷积操作中很好地捕获节点级表示。尤其是随着网络深度的增加,残差连接对模型的效果提升更加凸显。这种跳跃结构已经被证明可以显著提高模型在以节点相关任务上的性能,但是很少有研究人员探索它们在图级任务上(如图分类)的有效性。在GIN 中,Xu等人进一步提出了一种类似于JK-Net的模型架构用于学习图级表示。该架构针对每个卷积层后面都连接了一个读出层来学习不同深度的图级表示,然后将不同深度的图级表示形式连接在一起形成最终的表示。这种读出架构考虑了所有深度的全局信息,可以有效地改善模型的泛化能力。
2、图卷积神经网络(GCN)
(1)问题定义
给定一个无向图G = { V, E},V表示节点集合,E 表示边的集合。此外,使用Xv来表示每个节点的初始特征。图卷积神经网络的目标是学习任意图实例的连续表示,来对节点特征以及拓扑结构进行编码。假设给定了一组带有M个标签的图G = {G1, G2, ... ,GM}以及每一个图对应的标签Y = {y1, y2, ... ,yM},图分类的目标是使用它们作为训练数据来构建分类器gθ,该分类器可以将任何新的图输入G分配给某个特定的类别yG,即yG = gθ(hG)。
(2)图卷积神经网络
GCNs同时考虑图的结构信息和图中每个节点的特征信息,以学习可以最好地帮助完成最终任务的节点级和/或图级特征表示。通常来说,现有的GCN变体首先会聚
合邻域信息,然后将生成的邻域表示与上一次迭代的中心节点表示进行组合。从公式上来说,GCN根据以下公式迭代地更新节点的表示形式:
其中
表示的是节点v在第k次迭代时的特征表示。AGGREGATE()和COMBINE()都是第k 个图卷积层的可学习信息传递函数。N(v)表示节点v的相邻节点的集合。通常,在K次迭代步骤之后,可以将最终的节点表示
应用于节点标签预测,或者前进到执行图分类的读出阶段。读出阶段通过聚合节点特征,使用某些特定的读出函数READOUT()为整个图计算特征向量hG:
READOUT()函数可以是简单的置换不变性函数,例如求和函数;也可以是图级的池化操作,如DIFFPOOL、SORTPOOL。
3、方法介绍
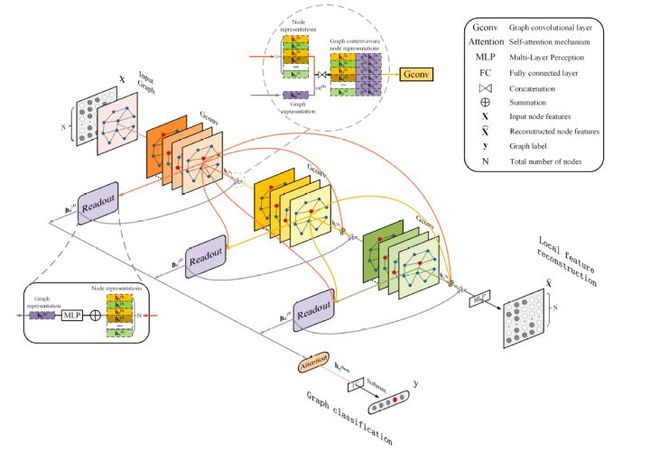
为了解决现有方法的局部信息保留能力和泛化能力不足的问题,这篇文章从损失函数和模型架构两个方面进行了改进,提出了模型LPD-GCN。众所周知,GCNs通过利用图的拓扑结构和节点特征来学习整个图的图级表示。从损失的角度来看,为了充分利用和学习节点的特征信息,LPD-GCN构造了额外的局部节点特征重构任务,以提高隐藏节点表示的局部表示能力并增强最终图级表示的判别能力。也就是额外增加了一个辅助约束来保留图的局部信息。这个节点特征重构任务是通过设计一种简单但有效的编码-解码机制来实现的,其中将堆叠的多个图卷积层当作编码器,然后添加一个多层感知器(MLP)用于后续的解码。这样的话,就可以将输入的节点特征通过编码器嵌入到隐藏表示中,然后将这些向量表示再输入到解码器中以重构初始节点特征。从模型架构的角度来看,首先探索并设计了一个稠密连接的图卷积架构来建立不同层之间的连接关系,以灵活充分地利用来自不同位置的邻域的信息。具体地说,将每个卷积层及其对应的读出模块与所有先前的卷积层相连。
(1)基于编码-解码机制的节点特征重构
传统GCN的图级表示能力和判别能力受限于过度精炼和全局化,忽视了对局部特征的保存,这会导致过平滑问题。LPD-GCN包含一个用于实现局部特征重构的简单的编码-解码机制,其中编码器由堆叠的多图卷积层构成,而解码器采用多层感知器来重构局部节点特征。同时,构造了一个辅助的局部特征重构损失来辅助图分类的目标。这样的话,节点特征可以有效地保留在不同层上的隐藏表示中。
(2)基于DenseNet的邻域聚合
此外,为了可以灵活地利用来自不同层的邻域的信息,模型从每个隐藏的卷积层到所有更高层的卷积层和读出模块都添加了直接的连接。这样的架构大致是DenseNets的对应结构。众所周知,DenseNets是针对计算机视觉问题提出的。该架构允许在不同层选择性地聚合邻域信息,并进一步改善层与层之间的信息流动。在DenseNets中应用的是分层串联的特征聚合方式。LPD-GCN采用分层累加的特征聚合方式。
(3)基于全局信息感知的局部节点表示
引入辅助的局部特征重构模块后,使得每个卷积层都可以接受额外的监督,以保持局部性。但是,此类监督信息无法通过反向传播来训练这些全局读出模块。在本章模型的架构中,在每个卷积层后面都有一个对应全局读出模块,来将整个图的节点嵌入折叠为图级别的表示。那么,如何才能更好地利用来自局部特征重构的监督信息呢?为了解决这个问题,添加了从每个读出模块到下一层卷积模块的直接连接,并使用串联的方式将节点级特征与全局图级特征进行对齐。也就是说,使用逐点串联,将每个节点表示和图级表示连接到单个张量中。此外,又引入了一个可学习的参数ε(> 0),以自适应地在局部节点级表示和全局图级表示之间进行权衡。
其中
通过设计这样的架构,除了因失去主图级任务而产生的梯度信息之外,还可因局部特征重构损失而使其他梯度信息反向传播以更新读出的参数,从而降低了丧失局部表示能力的风险并提高了模型的泛化能力。同时,节点表示与附加的全局上下文相结合以形成全局上下文感知的局部表示,这也可以增强节点的表示性。
(4)基于自注意力机制的全局分层聚合
现有的大部分方法是将多个图卷积层学习的节点表示馈送到全局读出模块以生成图级表示,读出模块通过池化或求和的方式生成全局的图级特征。但是,随着网络深度的增加,节点表示可能会显得过于平滑,从而导致图级输出的综合性能较差。为了有效地提取和利用所有深度的全局信息,本章的模型进一步采用了一种自注意力机制,以类似于GIN的方式来读出的逐层图级特征。这里引入以层为中心的自注意力机制的直觉是,在生成特定任务的图级输出时,分配给每一层不同的注意力权重可以适应于特定的任务。
(5)损失函数
在训练阶段,本章的模型LPD-GCN从图分类主任务和辅助的局部特征重构约束接收梯度信息。从公式上来说,通过如下公式中定义的总损失(由图分类损
失和局部特征重构损失加权得到)来训练LPD-GCN。
其中表示
图分类损失,
表示局部特征重构损失,权衡参数被自适应地引入在两个损失项之间寻求平衡。
4、图分类实验结果
(1)测试数据集
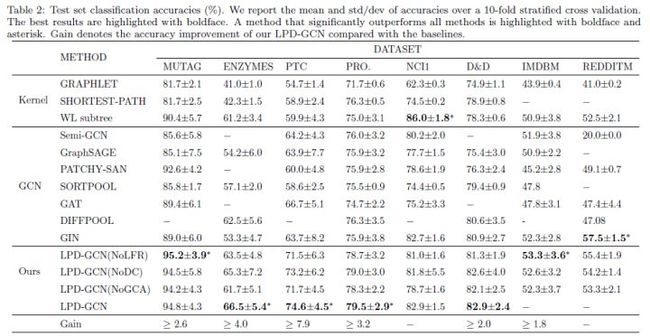
这篇文章使用了图神经网络领域8个常用的图数据集,通过执行10倍交叉验证来评估性能,并报告测试准确度的均值和标准差。
(2)在测试集上的效果
在多个数据集上的分类性能上有了明显的提升,且泛化能力得到了改善。
5、参考文献
[1] WENFENG LIU, MAOGUO GONG, ZEDONG TANG A. K. QIN. Locality Preserving Dense Graph Convolutional Networks with Graph Context-Aware Node Representations. https://arxiv.org/abs/2010.05404
[2] GILMER J, SCHOENHOLZ S S, RILEY P F, et al. Neural message passing for quantum chemistry[C] // Proceedings of the 34th International Conference on Machine Learning : Vol 70. 2017 : 1263 – 1272.
[3] XU K, HU W, LESKOVEC J, et al. How powerful are graph neural networks?[C] // Proceedings of the 7th International Conference on Learning Representations. 2019.
[4] VELI ˇ CKOVI´C P, CUCURULL G, CASANOVA A, et al. Graph attention networks[C] // Proceedings of the 6th International Conference on Learning Representations. 2018.
[5] YING Z, YOU J, MORRIS C, et al. Hierarchical graph representation learning with differentiable pooling[C] // Advances in Neural Information Processing Systems. 2018 : 4800 – 4810.
[6] XU K, LI C, TIAN Y, et al. Representation learning on graphs with jumping knowledge networks[C] // Proceeding of the 35th International Conference on Machine Learning. 2018 : 5449 – 5458.