概率图模型之（HMM）隐马模型（隐马尔可夫）

在讲隐马模型之前，首先要了解下，啥是马尔可夫模型。

马尔可夫模型

几个条件

当前状态只与前一个状态相关
一个状态到所有状态的转移概率和为1
概率大于等于0小于等于1
状态起始概率和为1
举个例子：
在文本中，假设有三个状态，名词n，动词v，形容词adj，三者之间的转移概率为(瞎编)：

初始化概率为p(adj) = 0.5，p(n)=0.3,p(v)=0.2.
那么，一个文本词性为形容词，名词，动词，名词的概率为：

相当于n-gram语言模型中，n = 2 的情况。

隐马尔可夫模型

在上述例子中，文本的词性是明确的，而隐马模型中，不知道所经历的状态序列，观察到的序列是随机的。所以，状态转换是随机的，观测序列也是随机的，双重随机过程。

举个例子：我吃饭。这里我们能够观测到的就是，‘我’，‘吃’，‘饭’。
那么‘我’对应的状态有‘动词’，‘名词’，‘形容词’，‘吃’，‘饭’同理。那么他们的背后词性序列，到底是名动名，还是动动名，还是形动名不得而知。这种未知序列称之为隐状态。
所以：隐马模型三要素，一个是状态转移矩阵（同上），另一个是观测状态到隐藏状态的概率矩阵。还有一个起始状态概率。

隐马模型的三个问题

如何计算观测序列O 的概率
如和计算观测序列O 最优的隐状态序列
参数如何学习

问题一：

这样相当于是穷举所有可能。即，O1的状态概率O2的状态概率状态之间的概率转移。这样，状态一多，观测长度一长，计算将会指数增长。
为了优化求解时间，采用动态规划的思想，即O1，到O2，在计算O2，到O3,一次类推，最终计算到Ot.
那么复杂度即，O1有N个状态，O2有N个状态，那么计算O1到O2，就需要计算N*N 次，最终算得N个路径，通往O3，解释有点绕。总共t次。随意复杂度为。具体算法可以查看 前向算法。大概样子就是如下所示：

问题二：

一般在问题二在NLP的应用中较多，需要找到当前观测序列最优的标注。
如何快速的找到最优的序列。
维特比算法：
算法原理这里不做阐述。这篇博客讲的非常通俗易懂～
https://blog.csdn.net/athemeroy/article/details/79339546
算法实现：
首先需要一个隐马模型：
写了个随机函数，生成隐马模型

def hmmRamdon():
    #隐状态个数
    yin_num = 5
    #观测概率个数
    guan_num = 10
    
    A = np.zeros((yin_num,yin_num))
    for i in range(yin_num):
        rows_h = np.random.random(yin_num)
        rows_v = np.random.random(yin_num)

        for k in range(i):
            rows_h[k] = A[i][k]

        rows_h[i:] = rows_h[i:] / rows_h[i:].sum() * (1 - rows_h[:i].sum())   
        A[i] = rows_h

        for k in range(i+1):
            rows_v[k] = A[k][i] 
        rows_v[i+1:] = rows_v[i+1:] / rows_v[i+1:].sum() * (1 - rows_v[:i+1].sum())

        for j in range(yin_num):
            A[j][i] = rows_v[j]
            
    
    B = np.zeros((yin_num,guan_num))
    for i in range(yin_num):
        row = np.random.random(guan_num)
        B[i] = row / row.sum()
    
    init_yin = np.random.random(yin_num)
    pai = init_yin / init_yin.sum()
    return A,B,pai

函数没有做大于0校验～，随出负数的话记得多随几次哈～

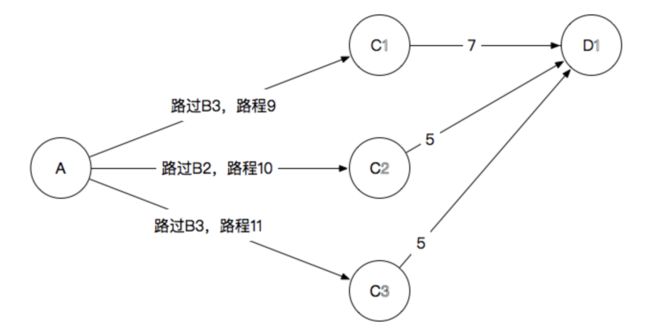
看过上述讲解维特比算法原理博客的同鞋，应该记得下图：

在HMM，中A->B相当于，观测序列的中第一个序列，B1->B3是隐状态，
所以当前A->B的路径可以初始化为
这里展示方便，假设HMM模型为

A = np.array([[0.5,0.2,0.3],
              [0.3,0.5,0.2],
              [0.2,0.3,0.5]])
B = np.array([[0.5,0.5],
              [0.4,0.6],
              [0.7,0.3]])
pai = np.array([[0.2,0.4,0.4]])

observe = [0,1,0]

a_ex = B[:,observe[0]] * pai
a_ex = a_ex.T 
all_way = np.full((yin_num, 1), -1)
print(a_ex)
print(all_way)
[[0.1 ]
 [0.16]
 [0.28]]
===========
[[-1]
 [-1]
 [-1]]

a_ex记录到达上一个观测状态每个隐状态最优的概率值。
observe[0]观测序列第一个，观测概率各自乘于初始化概率。all_way 用于记录每条路径经过的隐状态节点。0.1 = 0.5 * 0.2，0.16 = 0.4 * 0.4，0.28 = 0.7 * 0.4.
当计算由B->C时，C1，C2，C3 各自有三条路径，，结合A-B的路径，计算出A->C1概率最高的一条路径，同理计算到C2，C3的路径。

a_new = A1 *a_ex* B1[:,observe[1]]#计算图中9个路线
a_ex = np.amax(a_new,axis=0) #获取每个隐状态三个路径中最高的那一个
a_ex = a_ex.reshape(a_ex.shape[0],-1)
            
way = np.argmax(a_new,axis=0)#找出概率最高的三条路线
way = way.reshape(way.shape[0],-1)
all_way = np.hstack((all_way,way))#路径更新

a_new:
[[0.025  0.012  0.009 ]
 [0.024  0.048  0.0096]
 [0.028  0.0504 0.042 ]]
a_ex:
[[0.028 ]
 [0.0504]
 [0.042 ]]
all_way:
[[-1  2]
 [-1  2]
 [-1  2]]

所以对应图中的三条路径为A-B3-C1，A-B3-C2，A-B3-C3。
即博客中对应的图

如此循环直到最后一个。完整算法代码如下：

import numpy as np
def viterbi_search(A,B,pai,observe):
    yin_num = A.shape[0]
     
    for j in range(len(observe)):
        if j == 0:
            a_ex = B[:,observe[j]] * pai
            a_ex = a_ex.T 
            all_way = np.full((yin_num, 1), -1)
        else: 
            a_new = A1 *a_ex* B1[:,observe[j]]
            a_ex = np.amax(a_new,axis=0) 
            a_ex = a_ex.reshape(a_ex.shape[0],-1)

            way = np.argmax(a_new,axis=0)
            way = way.reshape(way.shape[0],-1)
            all_way = np.hstack((all_way,way)) 
            
    result = np.append(all_way[a_ex.argmax()],a_ex.argmax())
    
    return result, a_ex.max()

实验环境jupyter，实验代码下载链接：
链接:https://pan.baidu.com/s/1W9zckhKG3yssFeZtahl-5g 密码:78y5

问题三：参数估计

最大似然估计：
转移概率：aij = ai 到aj的次数 / ai到所有状态的次数。
观测概率：bi = ai 到 bi 观测的次数 / ai到所有观测的次数。

一般隐状态未知的情况下，可以用最大期望EM，对转移概率进行估计。