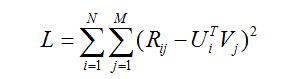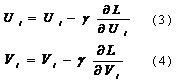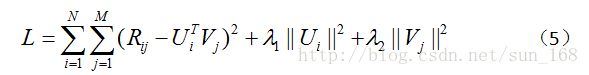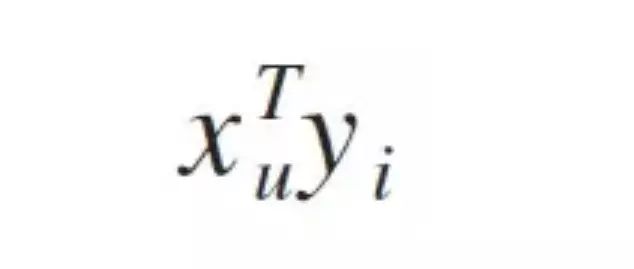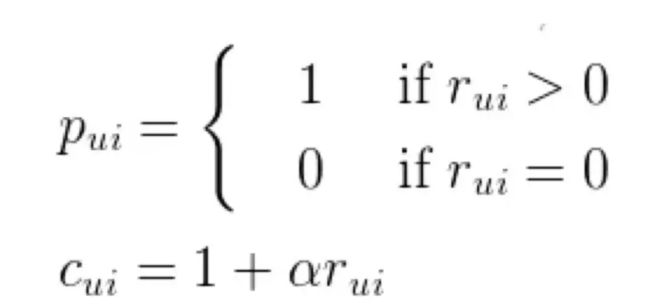机器学习矩阵分解解析Recommender.Matrix.Factorization

1.为什么要矩阵分解

2.矩阵分解怎么分解

3.什么样的情况考虑矩阵分解

4.矩阵分解有哪些分类

5.各种应用场景比较以及具体操作

6.评价总结

1.为什么要矩阵分解

矩阵分解是和以下故事有关：
啤酒和尿布的故事。
抖音和点赞的故事。
今日头条和你的故事。
网易云音乐和红心的故事。
推荐系统中最为主流与经典的技术之一是协同过滤技术（Collaborative Filtering），它是基于这样的假设：用户如果在过去对某些项目产生过兴趣，那么将来他很可能依然对其保持热忱。或者发挥集体的力量帮你做决策。
其中协同过滤技术又可根据是否采用了机器学习思想建模的不同划分为：
基于内存的协同过滤（Memory-based CF）与基于模型的协同过滤技术（Model-based CF）。其中基于模型的协同过滤技术中尤为矩阵分解（Matrix Factorization）技术最为普遍和流行，因为它的可扩展性极好并且易于实现，因此接下来我们将梳理下推荐系统中出现过的经典的矩阵分解方法。

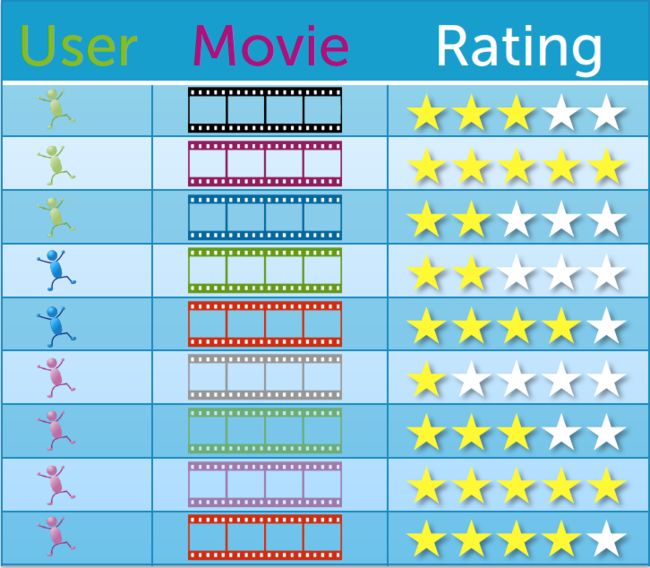
现在有一个用户对看过的电影的评分表：

机器学习矩阵分解解析Recommender.Matrix.Factorization_第1张图片

movie.png

绿色用户对3个电影做了评价,蓝色用户对2个电影做了评价,红色用户对4个电影做了评价.但无论多少个用户,相对大量的电影来说,每个用户只有可能看过很少的一部分电影.

机器学习矩阵分解解析Recommender.Matrix.Factorization_第2张图片

Matrix.png

如上图所示,黑点代表了用户u对电影v的评价,白点代表该用户没有对电影进行评价.
那么我们如何填充未知数据?
利用该用户历史数据和所有用户对该电影的评价数据。

2.矩阵分解怎么分解

预测一个人对从未看过的电影的评价:
我们需要用到2个向量:
电影类型向量:
　　假设
　　肖申克的救赎这部电影: 用动作相关值为0.3,与爱情相关值为0.01,与戏剧相关值为1.5
　　Rv = [ 0.3 0.01 1.5 ......]

用户偏好向量:

假设
　　用户A对电影的喜好:动作电影为2.5,爱情电影为0,戏剧电影为0.8
　　Lu-A = [ 2.5 0 0.8 ......]

那么Rating(u,v)的值为
　　0.3 * 2.5 + 0 + 1.5 * 0.8 + ...... = 7.2

假设B用户的Lu-B为 [ 0 3.5 0.01 ...... ]
　　0 + 0.013.5 + 1.50.01 + ...... = 0.8

很明显,A用户喜好这部电影的可能性更大.当然,一个电影最高评分为5分, 7.2显然没有体现分数的预测.上述方法（网易云潜在因子）可以预测出用户对电影的评价情况,但是有一个最主要的问题：
我们并不知道所有的Lu和Rv。

我们需要用到矩阵因子分解模型:
仍然使用残差平方和:
RSS(L,R) = (Rating(u,v) - )² + [ include all (u,v) ]
注意:后面中括号内的u,v指的是所有已经做出评价的u,v。

机器学习矩阵分解解析Recommender.Matrix.Factorization_第3张图片

image.png

3.什么情况需要考虑使用矩阵分解？（和PCA有什么不同）

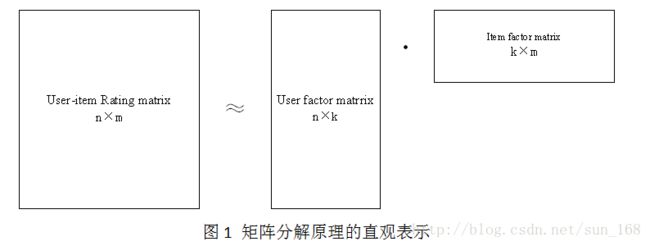
矩阵分解目标就是把用户-项目评分矩阵R分解成用户因子矩阵和项目因子矩阵乘的形式，即R=UV，这里R是n×m， n =6， m =7，U是n×k，V是k×m。直观地表示如下：

机器学习矩阵分解解析Recommender.Matrix.Factorization_第4张图片

矩阵分解直观解释

高维的用户-项目评分矩阵分解成为两个低维的用户因子矩阵和项目因子矩阵，因此矩阵分解和PCA不同， 不是为了降维。不是为了降维。不是为了降维。
用户i对项目j的评分r_ij =innerproduct(u_i, v_j)，更一般的情况是r_ij =f(U_i, V_j)，这里为了介绍方便就是用u_i和v_j内积的形式。

矩阵分解核心是：评估低维矩阵乘积拟合评分矩阵的方法。
先假设，用户对项目的真实评分和预测评分之间的差服从高斯分布，基于这一假设，可推导出目标函数如下：

机器学习矩阵分解解析Recommender.Matrix.Factorization_第5张图片

目标函数

最后得到矩阵分解的目标函数如下：

目标函数

从最终得到得目标函数可以直观地理解：
预测的分值就是尽量逼近真实的已知评分值。
预测的分值就是尽量逼近真实的已知评分值。
预测的分值就是尽量逼近真实的已知评分值。
有了目标函数之后，下面就开始谈优化方法了，通常的优化方法分为两种：交叉最小二乘法（alternative least squares）和随机梯度下降法（stochastic gradient descent）。

3.1 交叉最小二乘法

首先介绍交叉最小二乘法（als后面会详细说），之所以交叉最小二乘法能够应用到这个目标函数主要是因为L对U和V都是凸函数。首先分别对用户因子向量和项目因子向量求偏导，令偏导等于0求驻点，具体解法如下：

机器学习矩阵分解解析Recommender.Matrix.Factorization_第6张图片

交叉

上面就是用户因子向量和项目因子向量的更新公式，迭代更新公式即可找到可接受的局部最优解。迭代终止的条件下面会讲到。

3.2 随机梯度

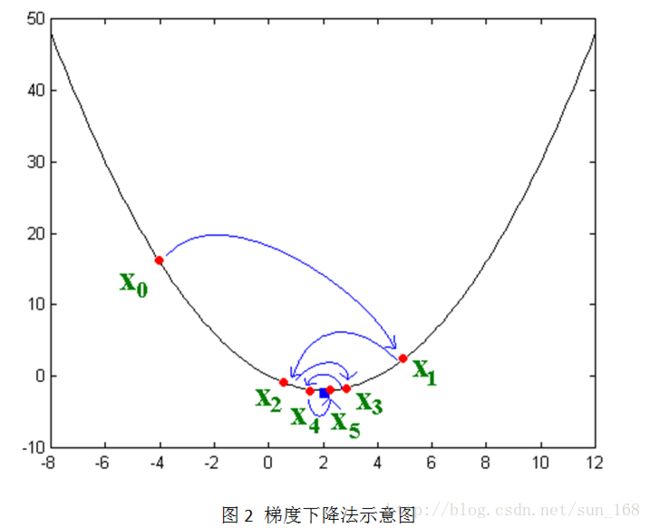
接下来讲解随机梯度下降法，这个方法应用的最多。大致思想是让变量沿着目标函数负梯度的方向移动，直到移动到极小值点。直观的表示如下：

机器学习矩阵分解解析Recommender.Matrix.Factorization_第7张图片

随机梯度-这个图真的很好，真的好，好

其实负梯度的负方向，当函数是凸函数时是函数值减小的方向走；当函数是凹函数时是往函数值增大的方向移动。而矩阵分解的目标函数L是凸函数，因此，通过梯度下降法我们能够得到目标函数L的极小值（理想情况是最小值）。

言归正传，通过上面的讲解，我们可以获取梯度下降算法的因子矩阵更新公式，具体如下：

image.png

（3）和（4）中的γ指的是步长，也即是学习速率，它是一个超参数，需要调参确定。对于梯度见（1）和（2）。

下面说下迭代终止的条件。迭代终止的条件有很多种，就目前我了解的主要有
　　1）设置一个阈值，当L函数值小于阈值时就停止迭代，不常用
　　2）设置一个阈值，当前后两次函数值变化绝对值小于阈值时，停止迭代
　　3）设置固定迭代次数

另外还有一个问题，当用户-项目评分矩阵R非常稀疏时，就会出现过拟合（overfitting）的问题，过拟合问题的解决方法就是正则化（regularization）。正则化其实就是在目标函数中加上用户因子向量和项目因子向量的二范数，当然也可以加上一范数。至于加上一范数还是二范数要看具体情况，一范数会使很多因子为0，从而减小模型大小，而二范数则不会它只能使因子接近于0，而不能使其为0，关于这个的介绍可参考论文Regression Shrinkage and Selection via the Lasso。引入正则化项后目标函数变为：

目标函数

（5）中λ_1和λ_2是指正则项的权重，这两个值可以取一样，具体取值也需要根据数据集调参得到。优化方法和前面一样，只是梯度公式需要更新一下。

3.3 矩阵分解和pca的区别

先说PCA，PCA降维的大致思想就是： 挑选特征明显的、显得比较重要的信息保留下来。也就是求动图中，在转动轴上的投影面积最大值。

机器学习矩阵分解解析Recommender.Matrix.Factorization_第8张图片

动图pca

那么关键就是【特征明显的，重要的信息】如何选择？选择标准有两个：
1：同一个维度内的数据，方差大的比较明显，因为方差大表示自己和平均水平差异大，有个性，降维后也最可能分的开～
2：两个不同维度间关联度越小越好，因为关联度小表示这两个维度表征共同信息的量比较少，最理想就是两个维度不相关，相关度为0（相关度可以用协方差cov(a,b)表示），在线性空间内表现为两个维度正交～

协方差矩阵的主对角线和其余元素正好可以分别表示方差和协方差，而根据两条标准又很容易想到求特征值和特征向量，推导过程覃含章写的很清楚了

似乎SVD好像解决同样的问题？
SVD(Singular Value Decomposition),奇异值分解,是一个能适用于任意的矩阵的一种分解的方法。
上面我们说PCA针对的是协方差矩阵C，但你得知道协方差矩阵是个方阵啊，难道不是方阵我们就不支持吗？？所以就有了SVD～～大概可以把SVD看作是对非方阵做PCA处理的一种方式啦，毕竟两者的套路都差不多，分解出特征值（SVD里是奇异值，数据XX‘的特征值的平方根），挑比较大的特征值对应的特征向量构成投影矩阵，然后做线性变换（将数据X投影到低维空间）

机器学习矩阵分解解析Recommender.Matrix.Factorization_第9张图片

svd

在几何中，我们可以把矩阵看做空间上的线性变换。SVD的几何含义是：对于任何的一个矩阵，我们都能找到一组坐标轴，它是由原来的坐标轴通过旋转和缩放得到的。奇异值的含义是：这组变换后新的坐标轴的长度。

SVD和PCA的关系。
相同：我们讲到要用PCA降维，需要找到样本协方差矩阵的最大的k个特征向量，然后用这最大的k个特征向量张成的矩阵来做低维投影降维。注意，SVD也可以得到协方差矩阵最大的k个特征向量张成的矩阵。
不同：但是SVD有个好处，有一些SVD的实现算法可以不求先求出协方差矩阵，也能求出右奇异矩阵VV。也就是说，PCA算法可以不用做特征分解，而是做SVD来完成。这也是为什么很多工具包中PCA算法的背后真正的实现是用的SVD，而不是我们认为的暴力特征分解。
另一方面，注意到PCA仅仅使用了我们SVD的右奇异矩阵，没有使用左奇异矩阵。而左奇异矩阵可以用于行数的压缩，右奇异矩阵可以用于列数，也就是PCA降维。

4.矩阵分解有哪些分类

这一部分先说大分类，在具体细说算法间的区别。

4.1 推荐系统来说存在两大场景即：

评分预测（rating prediction）与Top-N推荐（item recommendation，item ranking）。
评分预测场景主要用于评价网站，比如用户给自己看过的电影评多少分（MovieLens），或者用户给自己看过的书籍评价多少分（Douban）。其中矩阵分解技术主要应用于该场景。
Top-N推荐场景主要用于购物网站或者一般拿不到显式评分信息的网站，即通过用户的隐式反馈信息来给用户推荐一个可能感兴趣的列表以供其参考。其中该场景为排序任务，因此需要排序模型来对其建模。因此，我们接下来更关心评分预测任务。

4.1.1 评分预测任务

我们通常将用户和项目（以电影为例）表示为二维矩阵的形式，其中矩阵中的某个元素表示对应用户对于相应项目的评分，1-5分表示喜欢的程度逐渐增加，？表示没有过评分记录。推荐系统评分预测任务可看做是一个矩阵补全（Matrix Completion）的任务，即基于矩阵中已有的数据（observed data）来填补矩阵中没有产生过记录的元素（unobserved data）。值得注意的是，这个矩阵是非常稀疏的（Sparse），稀疏度一般能达到90%以上，因此如何根据极少的观测数据来较准确的预测未观测数据一直以来都是推荐系统领域的关键问题。

重点：推荐系统的评分预测场景可看做是一个矩阵补全的游戏，矩阵补全是推荐系统的任务，矩阵分解是其达到目的的手段。因此，矩阵分解是为了更好的完成矩阵补全任务（欲其补全，先其分解之）。之所以可以利用矩阵分解来完成矩阵补全的操作，那是因为基于这样的假设：假设UI矩阵是低秩的，即在大千世界中，总会存在相似的人或物，即物以类聚，人以群分，然后我们可以利用两个小矩阵相乘来还原它。

矩阵分解

该（评分）矩阵分解不像是线代中的分解，他属于伪分解。其主要思想是，用两个m＊k和k＊n的矩阵代替m＊n的矩阵。

评分矩阵分解

因为在推荐系统中，矩阵十分稀疏，分解后的矩阵一般是密集的，且可以通过行列相乘来得到空缺的值。其预测的是第u个用户对第i个商品的评分。

机器学习矩阵分解解析Recommender.Matrix.Factorization_第12张图片

u=用户，i=项目，xy=拆分矩阵，T=范围

通过线性的平方损失降低模型误差，通过正则减少拟合。
其学习方式有两种，一种是随机梯度下降，随处可见。
第二种是通过交替最小二乘。

4.1.2 Top-N推荐

我们一般的推荐问题不是通过评分推荐，因为评分的产生十分的困难，一般用户没有这个习惯。我们与其预测评分，不如去预测用户行为。如果我们给用户一个页面有十个商品，我们预测到用户会点击哪一个，这不就说明用户喜欢这个。而且基于用户的信息很多。

我们的矩阵由1，0和空缺组成，1表示该用户点击过该商品(即表示用户对它有想法)，0表示用户对它没有想法(怎么是没想法呢，我们定义用户知道他却不想了解他。即我们在所有没有点击该商品的用户中抽样，该商品越火热抽取的人越多。因为热门的东西大家应该都知道，而你却没点击他，说明他不感兴趣)

我们要将该矩阵分解，用的是隐式矩阵分解(最常见)ALS。我们先随机化一个Q，因为R是那个稀疏矩阵已知，所以能得到P，我们再反过来用PR求Q。直到模型的误差低于一个阈值。

机器学习矩阵分解解析Recommender.Matrix.Factorization_第13张图片

隐式矩阵分解

我们的损失函数是

机器学习矩阵分解解析Recommender.Matrix.Factorization_第14张图片

损失函数

对比svd我们多的参数
Rui指的是用户频率，它简单的把没有点击作为负样本比较不合适。
Cui是置信度，比如我点击10次当时比只点击一次的喜欢置信度高。

机器学习矩阵分解解析Recommender.Matrix.Factorization_第15张图片

als多的参数

对于学习方法，我们使用加权交替最小二乘法

机器学习矩阵分解解析Recommender.Matrix.Factorization_第16张图片

als学习方法

机器学习矩阵分解解析Recommender.Matrix.Factorization_第17张图片

带入整理得到

初始化Y，我们计算出x，再通过计算出y。再反复交替，直到小于阈值。

机器学习矩阵分解解析Recommender.Matrix.Factorization_第18张图片

计算合适阈值

4.2 各种矩阵分解对比

常见的推荐系统矩阵分解有BPR、SVD（funkSVD）、SVDFeature（陈天奇，xgboost的作者）、ALS、NMF、WRMF。接下来就来看看推荐系统中常用的几种矩阵分解的区别，主要通过公式、特点和适合哪种数据这几个方面来讲。

4.2.1. SVD

提到矩阵分解，人们首先想到的是数学中经典的SVD（奇异值）分解，直接上公式：

原理和流程
- 当然SVD分解的形式为3个矩阵相乘
- 左右两个矩阵分别表示用户/项目隐含因子矩阵
- 中间矩阵为奇异值矩阵并且是对角矩阵，每个元素满足非负性，并且逐渐减小
目的
- 推荐好
- 计算得到三个矩阵
- 左右两个矩阵分别表示用户/项目隐含因子矩阵
- 中间矩阵为奇异值矩阵并且是对角矩阵，每个元素满足非负性，并且逐渐减小
优点
- 在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。
- 也就是说，我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵
缺点
- 如果想运用SVD分解的话，有一个前提是要求矩阵是稠密的，即矩阵里的元素要非空，否则就不能运用SVD分解。很显然我们的任务还不能用SVD，所以一般的做法是先用均值或者其他统计学方法来填充矩阵，然后再运用SVD分解降维。
- 要求矩阵稠密
- 若用户和物品数据量大，计算量大，耗时长
- 冷启动没有解决

4.2.2.FunkSVD

刚才提到的 SVD 首先需要填充矩阵，然后再进行分解降维，同时由于需要求逆操作（复杂度O(n^3)），存在计算复杂度高的问题，所以后来Simon Funk提出了FunkSVD的方法，它不在将矩阵分解为3个矩阵，而是分解为2个低秩的用户项目矩阵，同时降低了计算复杂度，公式如下：

它借鉴线性回归的思想，通过最小化观察数据的平方来寻求最优的用户和项目的隐含向量表示。同时为了避免过度拟合（Overfitting）观测数据，又提出了带有L2正则项的FunkSVD：

以上两种最优化函数都可以通过梯度下降或者随机梯度下降法来寻求最优解。

FunkSVD小结

目的
- 推荐好
- 矩阵分解为2个低维矩阵
参数
- 无须加工
- 二元组
优点
- 思想简单
- 套用简单
- 模型的拓展性也很强，能够应用于各种场景
- 相比SVD计算复杂度降低
缺点
- 冷启动没有很好解决
- 数据稀疏

4.2.3.PMF

来自论文：Salakhutdinov et al. Probabilistic matrix factorization. NIPS(2008): 1257-1264.

PMF是对于FunkSVD的概率解释版本，它假设评分矩阵中的元素是由用户潜在偏好向量和物品潜在属性向量的内积决定的，并且服从均值为，方差为的正态分布：

则观测到的评分矩阵条件概率为：

同时，假设用户偏好向量与物品偏好向量服从于均值都为0，方差分别为的正态分布：
$\begin{aligned} p\left(U | \sigma_{U}^{2}\right) &=\prod_{i=1}^{N} \mathcal{N}\left(U_{i} | 0, \sigma_{U}^{2} \mathbf{I}\right) \\ p\left(V | \sigma_{V}^{2}\right) &=\prod_{j=1}^{M} \mathcal{N}\left(V_{j} | 0, \sigma_{V}^{2} \mathbf{I}\right) \end{aligned}$
根据贝叶斯公式，可以得出潜变量U,V的后验概率为：
$\begin{array}{l}{p\left(U, V | R, \sigma^{2}, \sigma_{V}^{2}, \sigma_{U}^{2}\right)=\frac{p\left(U, V, R, \sigma^{2}, \sigma_{V}^{2}, \sigma_{U}^{2}\right)}{p\left(R, \sigma^{2}, \sigma_{V}^{2}, \sigma_{U}^{2}\right)}=\frac{p\left(R | U, V, \sigma^{2}\right) \times p\left(U, V | \rho_{V}^{2}, \sigma_{U}^{2}\right)}{p\left(R, \sigma^{2}, \sigma_{V}^{2}, \sigma_{U}^{2}\right)}} \\ {\sim p\left(R | U, V, \sigma^{2}\right) \times p\left(U, V | \sigma_{V}^{2}, \sigma_{U}^{2}\right)} \\ {=p\left(R | U, V, \sigma^{2}\right) \times p\left(U | \sigma_{U}^{2}\right) \times p\left(V | \sigma_{V}^{2}\right)} \\ {=\prod_{i=1}^{N} \prod_{j=1}^{M}\left[N\left(R_{i j} | U_{i}^{T} V_{j}, \sigma^{2}\right)\right]^{I_{i j}} \times \prod_{i=1}^{N}\left[N\left(U_{i} | 0, \sigma_{U}^{2} I\right)\right] \times \prod_{j=1}^{M}\left[N\left(V_{j} | 0, \sigma_{V}^{2} I\right)\right]}\end{array}$
接着，等式两边取对数后得到：
$\begin{array}{l}{\ln p\left(U, V | R, \sigma^{2}, \sigma_{V}^{2}, \sigma_{U}^{2}\right)=-\frac{1}{2 \sigma^{2}} \sum_{i=1}^{N} \sum_{j=1}^{M} I_{i j}\left(R_{i j}-U_{i}^{T} V_{j}\right)^{2}-\frac{1}{2 \sigma_{U}^{2}} \sum_{i=1}^{N} U_{i}^{T} U_{i}-\frac{1}{2 \sigma_{V}^{2}} \sum_{j=1}^{M} V_{j}^{T} V_{j}} \\ {-\frac{1}{2}\left(\left(\sum_{i=1}^{N} \sum_{j=1}^{M} I_{i j}\right) \ln \sigma^{2}+N D \ln \sigma_{U}^{2}+M \operatorname{Dln} \sigma_{V}^{2}\right)+C}\end{array}$
最后，经过推导，我们可以发现PMF确实是FunkSVD的概率解释版本，它两个的形式一样一样的。

注：为了方便读者理解，在此举例推导中间项，将此项展开，带入多维正态分布即可得到。推导如下：

$\begin{aligned} & N\left(U_{i} | 0, \sigma_{U}^{2} I\right)=-\frac{1}{(2 \pi)^{D / 2}\left|\sigma_{U}^{2} I\right|^{1 / 2}} e^{-\frac{1}{2} \frac{1}{2} w_{i}^{T}\left(\sigma_{U}^{2} I\right)^{-1} U_{i}} \\ \ln N\left(U_{i} | 0, \sigma_{U}^{2} I\right) &=\ln \left(-\frac{1}{(2 \pi)^{D / 2}\left|\sigma_{U}^{2} I\right|^{1 / 2}}\right)-\frac{U_{i}^{T} U_{i}}{2 \sigma_{U}^{2}} \\=&-\ln \left(\left|\sigma_{U}^{2} I\right|^{1 / 2}\right)-\frac{U_{i}^{T} U_{i}}{2 \sigma_{U}^{2}}+C \\=&-\frac{1}{2} \ln \left(\sigma_{U}^{2 D}\right)-\frac{U_{i}^{T} U_{i}}{2 \sigma_{U}^{2}}+C \\=&-\frac{D}{2} \ln \left(\sigma_{U}^{2}\right)-\frac{U_{i}^{T} U_{i}}{2 \sigma_{U}^{2}}+C \end{aligned}$

PMF小结

目的
- 分数好
参数
- 无须加工
- 二元组
优点
- 思想简单
- 套用简单
- 模型的拓展性也很强，能够应用于各种场景
- 相比SVD计算复杂度降低
- PMF是对于FunkSVD的概率解释版
缺点
- 冷启动没有很好解决
- 数据稀疏

4.2.4. BiasSVD

来自论文：Koren et al. Matrix factorization techniques for recommender systems.Computer 42.8 (2009).

在FunkSVD提出来之后，陆续又提出了许多变形版本，其中相对流行的方法是BiasSVD，它是基于这样的假设：某些用户会自带一些特质，比如天生愿意给别人好评，心慈手软，比较好说话，有的人就比较苛刻，总是评分不超过3分（5分满分）；同时也有一些这样的项目，一被生产便决定了它的地位，有的比较受人们欢迎，有的则被人嫌弃，这也正是提出用户和项目偏置项的原因；项亮给出的解释是：对于一个评分系统有些固有属性和用户物品无关，而用户也有些属性和物品无关，物品也有些属性与用户无关，具体的预测公式如下：

其中，为整个网站的平均评分，是真个网站的基调；为用户的评分偏置，代表某个用户的评分基调，为项目的被评分偏置，代表某个项目的属性基调。

BiasSVD小结

目的：
- 分数好
参数：
- 二元组，无须处理
- BiasSVD假设评分系统包括三部分的偏置因素：
- 一些和用户物品无关的评分因素，用户有一些和物品无关的评分因素，称为用户偏置项。
- 而物品也有一些和用户无关的评分因素，称为物品偏置项
优点：
- BiasSVD增加了一些额外因素的考虑，因此在某些场景会比FunkSVD表现好。
- 电商或电影平台场景可能比较适合
缺点：
- 冷启动没有很好解决
- 数据稀疏

4.2.5.SVD++

来自论文：Koren Y. Factor in the neighbors: Scalable and accurate collaborative filtering[J]. ACM Transactions on Knowledge Discovery from Data (TKDD), 2010, 4(1): 1.

在用户除了显式评分外，隐式反馈信息同样有助于用户的偏好建模，因此随后提出了SVD++。它是基于这样的假设：用户除了对于项目的显式历史评分记录外，浏览记录或者收藏列表等隐反馈信息同样可以从侧面一定程度上反映用户的偏好，比如用户对某个项目进行了收藏，可以从侧面反映他对于这个项目感兴趣，具体反映到预测公式为：

其中为用户所产生隐反馈行为的物品集合；为隐藏的对于项目的个人喜好偏置，是一个我们所要学习的参数；至于是一个经验公式。

SVD++小结

目的：
- 推荐好
参数：
- 用户评分
- 用户点击
优点：
- SVD++增加了一些额外因素的考虑，如：用户行为不仅有评分，且有些隐反馈（点击等）。
- 视频平台、文章等媒体平台都适合，电商平台也适合
缺点：
- 冷启动没有很好解决
数据稀疏

4.2.6. timeSVD

来自论文：Koren et al. Collaborative filtering with temporal dynamics. Communications of the ACM 53.4 (2010): 89-97.

它是基于这样的假设：用户的兴趣或者偏好不是一成不变的，而是随着时间而动态演化。于是提出了timeSVD，其中用户的和物品的偏置随着时间而变化，同时用户的隐含因子也随着时间而动态改变，在此物品的隐含表示并未随时间而变化（假设物品的属性不会随着时间而改变）。

其中，为时间因子，表示不同的时间状态。

timeSVD小结

目的：
- 推荐好
参数：
- 用户评分
- 评分时间
优点：
- timeSVD++增加了一些额外因素的考虑，它假设用户爱好随时间的流动而变化
缺点：
- 冷启动没有很好解决
- 数据稀疏

4.2.7.NMF

来自论文：Lee et al. Learning the parts of objects by non-negative matrix factorization. Nature 401.6755 (1999): 788.

这是一篇发表在Nature上的经典论文，谷歌学术显示引用将近9k，它提出了一个假设：分解出来的小矩阵应该满足非负约束。

因为在大部分方法中，原始矩阵被近似分解为两个低秩矩阵相乘的形式，这些方法的共同之处是，即使原始矩阵的元素都是非负的，也不能保证分解出的小矩阵都为非负，这就导致了推荐系统中经典的矩阵分解方法可以达到很好的预测性能，但不能做出像User-based CF 那样符合人们习惯的推荐解释（即跟你品味相似的人也购买了此商品）。在数学意义上，分解出的结果是正是负都没关系，只要保证还原后的矩阵元素非负并且误差尽可能小即可，但负值元素往往在现实世界中是没有任何意义的。比如图像数据中不可能存在是负数的像素值，因为取值在0~255之间；在统计文档的词频时，负值也是无法进行解释的。因此提出带有非负约束的矩阵分解是对于传统的矩阵分解无法进行科学解释做出的一个尝试。它的公式如下：

其中， , 两个矩阵中的元素满足非负约束。

NMF小结

目的：
- 分数好
参数：
- 二元组，无须加工处理
优点：
- 分解出来的矩阵里的元素都是非负数
- 应用场景多，如下：
- NMF能被用于发现数据库中的图像特征，便于快速自动识别应用
- 能够发现文档的语义相关度，用于信息自动索引和提取
- 能够在DNA阵列分析中识别基因等等
- 最有效的就是图像处理领域，NMF是图像处理的数据降维和特征提取的一种有效方法。
缺点：
- 冷启动没有很好解决
- 数据稀疏

4.2.8.WMF

来自论文：Pan et al. One-class collaborative filtering. ICDM, 2008.
Hu et al. Collaborative filtering for implicit feedback datasets. ICDM, 2008.

对于矩阵分解来说，我们一般是处理的推荐系统中的评分预测任务，但同样矩阵分解也可以用来进行Top-N的推荐，即根据隐式信息来预测用户是否点击某项目。你可以把他看做是二分类问题，即点或者不点。但这不是普通的二分类问题，因为在模型训练的过程中负样本并非都为真正的负样本，可能是用户根本没见过该项目，何来喜不喜欢,没准他看到后喜欢呢，即正样本告诉我们作者喜欢的信息，但负样本并不能告诉我们该用户不喜欢。由于只存在正样本，所以我们把只有正反馈的问题定义为one-class问题，即单类问题。对于单类问题，该作者提出了两种解决策略，一种是加权的矩阵分解，另一种是负采样技术。虽然只是加了一下权重，看起来比较naive，但在于当时的研究背景下，这一小步其实是推荐系统中的一大步。

对于单类问题的研究一直没有停止过，虽然负采样技术是启发式的，即不用通过数据建模的方式来进行预测，但效果还是很好用的。最近几年人们提出了基于模型的方法来处理这种单类问题，即从缺失数据中来进行建模，具体可参见这两篇论文【Hernández-Lobato et al 2014，Liang et al 2016】。

WMF小结

目的：
- 推荐好
参数：
- 用户评分、点击、评论等操作，这些操作都转换为 0或1 数据
- 还要对样本进行负采样
优点：
- 符合TopN推荐
- 采用了用户的隐性数据
缺点：
- 冷启动没有很好解决
- 数据稀疏

4.2.9.LLORMA

来自论文：Lee et al. Local low-rank matrix approximation.ICML. 2013.

经典的矩阵分解模型是假设整个用户-项目矩阵（即UI矩阵）满足低秩假设（即全局低秩假设），即在整个系统当中，用户和项目总是满足存在相似的某种模式，即物以类聚，人以群分。

这种假设固然有道理，但在当今大数据时代下，全局意义上的低秩假设似乎太强了，尤其是在数据量巨大的情况下（即用户数与项目数都很多的系统当中），因此该论文推翻了全局意义上经典的全局低秩假设，它认为大千世界，林林总总，我们应该去寻找局部的低秩假设（即局部低秩假设）。首先根据某种相似测度来将整个大矩阵分为若干个小矩阵，每个小矩阵当中满足某种相似度阈值，然后再在局部的小矩阵当中做低秩假设。这样，全局的大矩阵可以由多个局部的小矩阵来加权组合构成，具体可参见该论文。

机器学习矩阵分解解析Recommender.Matrix.Factorization_第19张图片

LLORMA

LLORMA小结

目的：
- 推荐好
参数：
- 输入:评分矩阵
- 局部模型个数q,局部矩阵的秩r,学习速率ν,正则化参数λ.
优点：
- 计算复杂度保证了LLORMA算法具有计算上的高效性
- 并且LLORMA算法可以应用于大规模数据推荐场景.
缺点：
- 暂时不知

4.2.10.SRui

来自论文：Ma Hao. An experimental study on implicit social recommendation. SIGIR, 2013.

虽然经典的矩阵分解方法已经可以到达比较好的预测性能了，但它固有的弊病仍然是躲不开的，即数据稀疏与冷启动问题。为了缓解数据稀疏我们可以引入丰富的社交信息。即如果两个用户是朋友关系，那么我们假设他们有相同的偏好，同时他们学得的用户隐表示在向量空间应该有相近的距离。用户维度如此，同理，项目维度亦可以利用此思路来约束项目隐表示。即如果两个项目之间的关系较近，那么在低维向量空间中的距离同样也应该较小。这里的项目关系是从UI矩阵中抽取出来的，论文中成为项目隐社交关系（其实项目维度跟社交没啥关系）。具体公式如下：
$\begin{aligned} L=& \min _{U, V} \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{n} I_{i j}\left(r_{i j}-\mathbf{u}_{i}^{T} \mathbf{v}_{j}\right)^{2} \\ &+\frac{\alpha}{2} \sum_{i=1}^{m} \sum_{f \in \mathcal{F}^{+}(i)} s_{i f}\left\|\mathbf{u}_{i}-\mathbf{u}_{f}\right\|_{F}^{2} \\ &+\frac{\beta}{2} \sum_{j=1}^{n} \sum_{q \in \mathbb{Q}^{+}(j)} s_{j q}\left\|\mathbf{v}_{j}-\mathbf{v}_{q}\right\|_{F}^{2} \\ &+\frac{\lambda_{1}}{2}\|U\|_{F}^{2}+\frac{\lambda_{2}}{2}\|V\|_{F}^{2} \end{aligned}$
其中，表示用户和用户的社交相似度，表示项目与项目的隐社交相似度，在用户维度和项目维度分别增加了平滑项约束，使得学得的隐特征表示更加符合现实意义。

SRui小结

目的：
- 推荐好
参数：
- 评分矩阵
优点：
- 针对有用户之间交互的场景进行了优化
- 针对项目之间也有优化
- 丰富了数据，对数据稀疏有缓解
缺点：
- 数据稀疏
- 冷启动问题

4.2.11. ConvMF

来自论文：Kim et al. Convolutional matrix factorization for document context-aware recommendation. RecSys 2016.

当然矩阵分解的优点之一是可扩展性好，这当然不是吹的，比如16年的这篇文章就是将矩阵分解（MF）与图像处理领域很火的卷积神经网络（CNN）做了完美结合。

矩阵分解作为协同过滤模型中经典的方法，性能当然没的说。但它存在的数据稀疏与冷启动问题一直以来都是它的痛点，因此结合外部丰富的信息成为了缓解上述问题的有效途径。其中文本数据作为web中主流的数据形式成为了首选，并且对于文本的处理，大部分还是基于one-hot的表示，因此无法捕捉文档中上下文的关键信息，于是作者将两者做了结合，具体细节请参见论文，该公式如下：
$\begin{array}{c}{\mathcal{L}(U, V, W)=\sum_{i}^{N} \sum_{j}^{M} \frac{I_{i j}}{2}\left(r_{i j}-u_{i}^{T} v_{j}\right)_{2}+\frac{\lambda_{U}}{2} \sum_{i}^{N}\left\|u_{i}\right\|_{2}} \\ {\quad+\frac{\lambda_{V}}{2} \sum_{j}^{M}\left\|v_{j}-\operatorname{cnn}\left(W, X_{j}\right)\right\|_{2}+\frac{\lambda_{W}}{2} \sum_{k}^{\left|w_{k}\right|}\left\|w_{k}\right\|_{2}}\end{array}$
其中，在使得用户隐向量与项目隐向量做内积尽可能逼近真实评分的同时，对项目隐向量做了额外约束，即让项目隐向量跟CNN学得的文档特性尽可能的接近。

ConvMF小结

目的：
- 分数好
参数：
- 评分矩阵
- 文本数据，如评论等
优点：
- 丰富了数据集，缓解数据稀疏问题
- 在使得用户隐向量与项目隐向量做内积尽可能逼近真实评分的同时
- 对项目隐向量做了额外约束，即让项目隐向量跟CNN学得的文档特性尽可能的接近
缺点：
- 冷启动问题

4.2.12.NCRPD-MF

来自论文：Hu et al. Your neighbors affect your ratings: on geographical neighborhood influence to rating prediction. SIGIR 2014.

刚才说到，MF的可扩展性好，一方面是可以和主流模型做无缝集成，另一方面是可以和多种信息源做特征融合，比如14年的这篇文章，它是融合了文本评论信息，地理邻居信息，项目类别信息以及流行度等信息，具体预测公式如下：
$\begin{aligned} \hat{r}_{u i} &=\mu+b_{u}+b_{i} \\ &+\mathbf{p}_{u}^{\top}\left(\frac{1}{\left|R_{i}\right|} \sum_{w \in R_{i}} \mathbf{q}_{w}+\frac{\alpha_{1}}{\left|N_{i}\right|} \sum_{n \in N_{i}} \mathbf{v}_{n}+\frac{\alpha_{2}}{\left|C_{i}\right|} \sum_{c \in C_{i}} \mathbf{d}_{c}\right) \end{aligned}$

其中，为文本特征的低维向量表示，为地理邻居的低维向量表示，为项目类别的低维特征表示。

NCRPD-MF小结

目的：
- 推荐好
参数：
- 评分矩阵
- 文本数据，如评论等
- 地理数据
优点：
- 丰富了数据集，缓解数据稀疏问题
- 针对大众交互多的，点评平台。如：大众点评
- 这些平台都具有丰富的文本和地理信息
缺点：
- 暂时不知

4.2.13.ALS

通过之前构建目标函数之后，就要用到优化算法找到能使它最小的参数。优化方法常用的选择有两个，一个是随机梯度下降(SGD)，另一个是交替最小二乘(ALS),在实际应用中，交替最小二乘更常用一些，这也是推荐系统中选择的主要矩阵分解方法。
找到两个矩阵P和Q，让它们相乘后约等于原矩阵R:

als

P和Q两个都是未知的，如果知道其中一个的话，就可以按照代数标准解法求得，比如知道Q，那么P就可以这样算：

advantage

也就是R矩阵乘Q矩阵的逆矩阵就得到了结果，反之，知道了P 再求Q 也一样，交替最小二乘通过迭代的方式解决这个鸡生蛋蛋生鸡的难题：
1)、初始化随机矩阵Q里面的元素值

2)、把Q矩阵当做已知的，直接用线性代数的方法求得矩阵P

3)、得到了矩阵P后，把P当做已知的，故技重施，回去求解矩阵Q

4)、上面两个过程交替进行，一直到误差可以接受为止

ALS小结

目的：
- 推荐好
参数：
- 评分矩阵
- 文本数据，如评论等
- 地理数据
优点：
- 在交替的其中一步，也就是假设已知其中一个矩阵求解另一个时，要优化的参数是很容易并行的；
- 在不是很稀疏的数据集合上，交替最小二乘通常比随机梯度下降要更快的得到结果。
缺点：
- p@k，ndcg很低，mse不错

4.2.14. BPR&SVDfeature

BPR
在很多推荐场景中，我们都是基于现有的用户和商品之间的一些数据，得到用户对所有商品的评分，选择高分的商品推荐给用户，这是funkSVD之类算法的做法，使用起来也很有效。但是在有些推荐场景中，我们是为了在千万级别的商品中推荐个位数的商品给用户，此时，我们更关心的是用户来说，哪些极少数商品在用户心中有更高的优先级，也就是排序更靠前。也就是说，我们需要一个排序算法，这个算法可以把每个用户对应的所有商品按喜好排序。BPR就是这样的一个我们需要的排序算法。

BPR根据像交替最小二乘那样完成矩阵分解，先假装矩阵分解结果已经有了，于是就计算出用户对于每个物品的推荐分数，只不过这个推荐分数可能并不满足均方根误差最小，而是满足物品相对排序最佳

得到了用户和物品的推荐分数后，就可以计算四元组的样本中，物品1和物品2的分数差，这个分数可能是正数，也可能是负数，也可能是0。如果物品1和物品2相对顺序为1，那么希望两者分数之差是个正数，而且越大越好；如果物品1和物品2的相对顺序是0，则希望分数之差是负数，且越小越好。
目标函数：

bpr

SVDFeature
SVDFeature 是由上海交大Apex Data & Knowledge Management Lab(APEX)开发的一个推荐系统工具包。他们提出了一种基于feature 的矩阵分解的框架。

它的目的是有效地解决基于特征的矩阵分解。新的模型可以只通过定义新的特征来实现。

这种基于特征的设置允许我们把很多信息包含在模型中，使得模型更加与时俱进。使用此工具包，可以很容易的把其他信息整合进模型，比如时间动态，领域关系和分层信息。除了评分预测，还可以实现pairwise ranking任务。

SVDFeature的模型定义如下：

svd

输入包含三种特征<α，β，γ>，分别是用户特征，物品特征和全局特征。

5.各种应用场景比较以及具体操作

下面说一下我使用上的区别：
SVD：
基于现有的用户和商品之间的一些数据，得到用户对所有商品的评分，选择高分的商品推荐给用户，可以根据以往的评分矩阵做全局的评分优化。要求矩阵是稠密的，时间复杂度高。不推荐使用。
有多种从SVD的改进算法可选择，如：
FunkSVD：不在将矩阵分解为3个矩阵，而是分解为2个低秩的用户项目矩阵，同时降低了时间复杂度。
BiasSVD：考虑偏置项时使用，也就是用户的爱好。
SVD++：考虑用户的隐式反馈时使用。主动点评电影或者美食的用户是少数，也就是说显示反馈比隐式反馈少，这个时候就可以根据用户的隐式反馈推荐。
timeSVD：考虑时间因素时使用。人是善变的，随着时间的流逝，兴趣也会发生变化。
SVDFeature：当我们有多个特征时，可以使用。SVDFeature的目的就是解决基于特征的矩阵分解。

ALS：
ALS算法和SVD的使用场景相似，也是基于用户——商品评分数据得到全局用户对商品的评分。但是ALS算法是无法准确评估新加入的用户或商品。这个问题也被称为冷启动问题。
建模时间如果要求短，强烈推荐使用，这也是 Facebook 在他们的推荐系统中选择的主要矩阵分解算法。

NMF：
要用NMF做矩阵分解有一个很大的前提——用户item之间的评分矩阵要求是非负并且分解出的小矩阵也要满足非负约束。NMF分解是对原矩阵的近似还原分解，其存在的问题和ALS相像，对于未知的评分预测相当不准确。NMF用法和SVD、ALS相似。

BPR：
BPR是基于矩阵分解的一种排序算法，但是，它不是做全局的评分优化，而是针对每一个用户自己的商品喜好分贝做排序优化。因此在迭代优化的思路上完全不同。BPR需要用户对商品的喜好排序三元组做训练集。简单的说：考虑排序结果时使用。

WRMF：
当没有得到用户具体的评分，但是能够得到一些类似于隐式反馈信息时，就可使用WRMF进行矩阵分解。

总结
首先因为低秩假设，一个用户可能有另外一个用户与他线性相关（物品也一样），所以用户矩阵完全可以用一个比起原始UI矩阵更低维的矩阵表示，pureSVD就可降维得到两个低维矩阵，但是此方法要求原始矩阵稠密，因此要填充矩阵（只能假设值），因此有了funkSVD直接分解得到两个低维矩阵。因为用户,物品的偏置爱好问题所以提出了biasSVD。因为用户行为不仅有评分，且有些隐反馈（点击等），所以提出了SVD++。因为假设用户爱好随时间变化，所以提出了timeSVD。因为funkSVD分解的两个矩阵有负数，现实世界中不好解释，所以提出了NMF。为了符合TopN推荐，所以提出了WMF。推翻低秩假设，提出了LLORMA（局部低秩）。因为以上问题都未解决数据稀疏和冷启动问题，所以需要用上除了评分矩阵之外的数据来使推荐更加丰满，即加边信息。

6.评价总结

6.1评价的几种指标

1. P@K
P@K，代表前 K 个预测值中有多少的准确率 (Precision)。
比如，一个模型输出了一组排序，其输出的好坏依次为：好、坏、好、坏、好。
那么，
Prec@3 = 2/3
Prec@4 = 2/4
Prec@5 = 3/5

def precision(gt, pred, K):
    """ Computes the average precision.
        gt: list, ground truth, all relevant docs' index
        pred: list, prediction
    """
    hit_num = len(gt & set(pred[:K]))
    return float(1.0 * hit_num / K)

2. MAP
AP 是 average precision 的缩写，计算方式是把所有相关文档的 P@K 求平均。
借用上面的例子，一个模型输出了一组排序，依次为：好的结果、坏的结果、好的结果、坏的结果、好的结果。
那么，
AP = (1/1 + 2/3 + 3/5) / 3 = 0.76
注意，不是 (1/1 + 1/2 + 2/3 + 2/4 + 3/5) / 5。因为在实际情况中，总有一些"好的结果"是模型漏召回的，指标的计算公式应该怎么处理这部分漏召回？
AP 会把所有"好的结果"都算上，但是排序模型可能会对某些"好的结果"漏召回，这些"漏召回"的 P@K 视为0。MAP 是 mean average precision 的缩写，就是把所有的 AP 求平均。

def average_precision(gt, pred):
    """ Computes the average precision.
        gt: list, ground truth, all relevant docs' index
        pred: list, prediction
    """
    if not gt:
        return 0.0

    score = 0.0
    num_hits = 0.0
    for i, p in enumerate(pred):
        if p in gt and p not in pred[:i]:
            num_hits += 1.0
            score += num_hits / (i + 1.0)

    return score / max(1.0, len(gt))

3. MRR
某些场景下，每个问题只有一个标准答案，我们只关心标准答案的排序位置。此时，我们是把标准答案在模型输出结果中的排序取倒数作为它的 RR (Reciprocal Rank)。
比如，模型的输出一组排序，依次为：非标准答案，标准答案，非标准答案，非标准答案,那么：
RR = 1/2
对所有的问题取平均，得到 MRR (Mean Reciprocal Rank)。

def reciprocal_rank(gt, pred):
    """ Computes the reciprocal rank.
        gt: list, ground truth, all relevant docs' index
        pred: list, prediction
    """
    if not gt:
        return 0.0

    score = 0.0
    for rank, item in enumerate(pred):
        if item in gt:
            score = 1.0 / (rank + 1.0)
            break
    return score

4. NDCG
这块涉及到一些数学公式，我懒得打了，可以谷歌到。直接看下面的代码来理解估计会更清楚一些。
DCG: Discounted Cumulative Gain
IDCG: ideal DCG，是 ground truth 情况下的 DCG
NDCG: normalized DCG，是 DCG 和 IDCG 相除
NDCG = DCG / IDCG

def NDCG(gt, pred, use_graded_scores=False):
    """ Computes the NDCG.
        gt: list, ground truth, all relevant docs' index
        pred: list, prediction
    """
    score = 0.0
    for rank, item in enumerate(pred):
        if item in gt:
            if use_graded_scores:
                grade = 1.0 / (gt.index(item) + 1)
            else:
                grade = 1.0
            score += grade / np.log2(rank + 2)

    norm = 0.0
    for rank in range(len(gt)):
        if use_graded_scores:
            grade = 1.0 / (rank + 1)
        else:
            grade = 1.0
        norm += grade / np.log2(rank + 2)
    return score / max(0.3, norm)

5. 精度和召回率
召回率:　#liked & shown / #liked
精度：　#liked & show / #shown

如果所有商品都进行推荐,召回率变成了1,但是精度变得非常小.
最佳的性能: 精度 = 1,召回率 = 1

机器学习矩阵分解解析Recommender.Matrix.Factorization_第20张图片

image

不同算法之间进行比较:
曲线下的面积最大的,就是最优性能。

6. 均方误差
方误差（mean-square error, MSE）是反映估计量与被估计量之间差异程度的一种度量。设t是根据子样确定的总体参数θ的一个估计量，(θ-t)²的数学期望，称为估计量t的均方误差。它等于σ²+b²，其中σ²与b分别是t的方差与偏倚。
MSE是衡量“平均误差”的一种较方便的方法，MSE可以评价数据的变化程度，MSE的值越小，说明预测模型描述实验数据具有更好的精确度。求解方式为，各随机变量与平均值差值的平方和的平均数（先求差，再平方，再平均）

机器学习矩阵分解解析Recommender.Matrix.Factorization_第21张图片

mse

6.2评价指标测试以及分析

github上开源数据对几种算法评价分析：https://github.com/microsoft/recommenders
虽然很多算法论文用的pk或者ndcg作为评价指标，但是测试发现矩阵分解的普遍p@k较低

机器学习矩阵分解解析Recommender.Matrix.Factorization_第22张图片

benchmark

原因是（推荐系统36式）：

机器学习矩阵分解解析Recommender.Matrix.Factorization_第23张图片

比较

pk追求的是评分最优，而mse追求的全局最优。

总的来说，矩阵分解算法目前在推荐系统中应用非常广泛，对于使用RMSE作为评价指标的系统尤为明显，因为矩阵分解的目标就是使RMSE取值最小。但矩阵分解有其弱点，就是解释性差，不能很好为推荐结果做出解释。

参考：
https://www.cnblogs.com/bugutian/p/11288673.html
https://www.cnblogs.com/redheat/p/9367222.html
推荐系统中的矩阵分解https://blog.csdn.net/qq_19446965/article/details/82079367
spark的alshttp://spark.apache.org/docs/1.5.2/mllib-collaborative-filtering.html#collaborative-filtering
矩阵分解对比https://www.jianshu.com/p/0bb8c470326b
通俗的理解矩阵分解的意义https://blog.csdn.net/xuejianxinokok/article/details/79230190
SVD矩阵分解考虑时间因素（去噪声，值得一看）https://blog.csdn.net/shuaishuai3409/article/details/51284060
硕士论文-考虑评论的矩阵分解https://www.ixueshu.com/document/79da8b70f0a1bdba53059029ef3fbcb4318947a18e7f9386.html
两种分解方法https://www.cnblogs.com/hxsyl/p/4881453.html
一文理解矩阵特征值、特征向量、矩阵分解、pca、svd的来龙去脉https://blog.51cto.com/yixianwei/2156128](https://blog.51cto.com/yixianwei/2156128

机器学习矩阵分解解析Recommender.Matrix.Factorization

1.为什么要矩阵分解

2.矩阵分解怎么分解

3.什么样的情况考虑矩阵分解

4.矩阵分解有哪些分类

5.各种应用场景比较以及具体操作

6.评价总结

1.为什么要矩阵分解

2.矩阵分解怎么分解

3.什么情况需要考虑使用矩阵分解？（和PCA有什么不同）

3.1 交叉最小二乘法

3.2 随机梯度

3.3 矩阵分解和pca的区别

4.矩阵分解有哪些分类

4.1 推荐系统来说存在两大场景即：

4.1.1 评分预测任务

4.1.2 Top-N推荐

4.2 各种矩阵分解对比

4.2.1. SVD

4.2.2.FunkSVD

4.2.3.PMF

4.2.4. BiasSVD

4.2.5.SVD++

4.2.6. timeSVD

4.2.7.NMF

4.2.8.WMF

4.2.9.LLORMA

4.2.10.SRui

4.2.11. ConvMF

4.2.12.NCRPD-MF

4.2.13.ALS

4.2.14. BPR&SVDfeature

5.各种应用场景比较以及具体操作

6.评价总结

6.1评价的几种指标

6.2评价指标测试以及分析

你可能感兴趣的:(机器学习矩阵分解解析Recommender.Matrix.Factorization)