在多要素所构成的系统中,当研究某一个要素对另一个要素的影响或相关程度时,把其他要素的影响视作常数(保持不变),即暂时不考虑其他要素影响,单独研究两个要素之间的相互关系的密切程度,所得数值结果为偏相关系数。也就是我们在论文中看到的control variables(Age, educateion, gender)等与实验无关的变量Z,但是又影响因变量Y。
在多元回归分析中,在消除其他变量影响的条件下,所计算的某两变量之间的相关系数。在多元相关分析中,简单相关系数可能不能够真实的反映出变量X和Y之间的相关性,因为变量之间的关系很复杂,它们可能受到不止一个变量的影响。这个时候偏相关系数是一个更好的选择。
假设我们需要计算X和Y之间的相关性,Z代表其他所有的变量,X和Y的偏相关系数可以认为是X和Z线性回归得到的残差Rx与Y和Z线性回归得到的残差Ry之间的简单相关系数,即pearson相关系数。
得到便相关系数partial correlation coefficient。 x,y是想要分析相关的变量,z是想要control的变量。
R,Matlab 和spss上实现:
R method 1:借助工具包“dplyr"里面的函数pcor.test
library(dplyr)
stats2 <- pcor.test(X,Y,Z,method="pearson")
methods:"pearson", "spearman","kendall"
Results:
R method 2:用定义,借助工具包“stats"里面的cor.test,lm,residuals函数
library(stats)
r1 <- residuals(lm(formula=X~Z))
r2 <- residuals(lm(formula=Y~Z))
stats3 <- cor.test(r1,r2,method="pearson")
这样写lm 函数,线性回归拟合的方程为:X=B1*Z+B01; Y= B2*Z+B02, 默认线性回归的函数是有截距的。
Results:
Matlab:利用partialcorr 函数
[rho,p_value] = partialcorr(X,Y,Z,'type','Pearson');
Results:
Matlab method 2:用回归误差相关的思路来求偏相关系数(错误代码示例)
[B1,BINT1,R1,RINT1] = regress(X,Z);
[B2,BINT2,R2,RINT2] = regress(Y,Z);
[rho,p_value] = corr(R1,R2,'type','Pearson');
这样写regress 函数,线性回归拟合的方程为:X=B1*Z; Y= B2*Z,默认回归函数没有截距。
Results:
注意:结果不一样,貌似做了同样的事情,得不到相同的结果。其实是因为Matlab regress函数的特殊用法,需要一个全一向量来占位b0
正确代码示例
[B1,BINT1,R1,RINT1] = regress(X,[ones(size(Z,1),1),Z]);
[B2,BINT2,R2,RINT2] = regress(Y,[ones(size(Z,1),1),Z]);
[rho,p_value] = corr(R1,R2,'type','Pearson');
这样写regress 函数,线性回归拟合的方程为:X=B1(1,1)*1+B1(1,2)*Z; Y= B2(1,1)*1+B2(1,2)*Z. 由于regress默认回归函数没有截距,所以要自己添加一个全1的向量,回归结果中这个时候B1(1,2)(B2(1,2))才是变量Z的系数,B1(1,1)(B1(1,2))是截距.
Results:结果与上面一致了
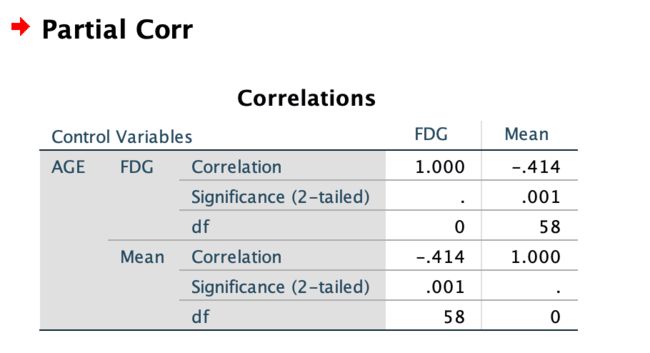
SPSS:
Results: