I believe I can fry！！！
QYommfvj.jpg
2.all about the base
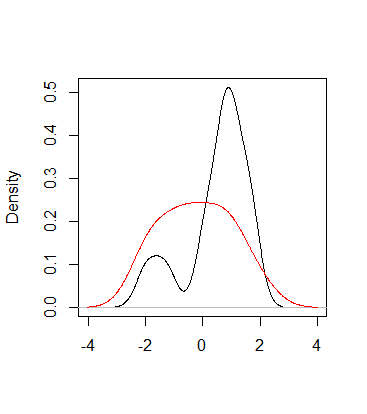
- 问怎么把两个密度图放在一起？
- 主要是x轴和y轴坐标的设置；
- range对应
density（）$x和density（）$y均计算出min和max；- lines在原有的图上进行
density结果的绘制；
set.seed(0704)
e <- data.frame(data=rnorm(25),sub=rep(c(1,2),c(12,13)))
xr<- range(density(e[e$sub==1,'data'])$x,density(e[e$sub==2,'data'])$x)
yr <- range(density(e[e$sub==1,'data'])$y,density(e[e$sub==2,'data'])$y)
plot(density(e[e$sub==1,'data']),xlim=xr,ylim=yr,main=' ',xlab=' ')
lines(density(e[e$sub==2,'data']),col=2)
two
- 多图展示-layout
matrix是对图片位置的设定，将图片进行3x3的划分；其中第一行是1，第二行和第3行均是2,3,4；widths和heights协同对上述9宫格的size进行设置；
layout(matrix(c(1,1,1,2,3,4,2,3,4),3,3,
byrow = T),widths=c(2,2,2),heights=c(2,1,3))
layout.show(n=4)
hist(rnorm(25),col= 1,main='1')
hist(rnorm(25),col= 2,main='2')
hist(rnorm(25),col= 3,main='3')
hist(rnorm(25),col= 4,main='4')
layout.png
image.png
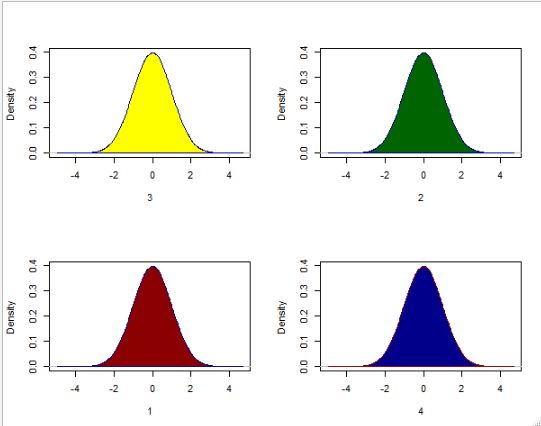
- 多图展示-par
par的fig参数，格式为c(x1, x2, y1, y2)，通过4个数字设置了图片的位置和大小，new=TRUE表示在图片上进行新图的绘制；
fig <- density(rnorm(200000))
par(fig=c(0,0.5,0,0.5))
plot(fig,main='',xlab='1')
polygon(fig,col='darkred',border='darkblue')
par(fig=c(0.5,1,0.5,1),new=TRUE)
plot(fig,main='',xlab='2')
polygon(fig,col='darkgreen',border='darkblue')
par(fig=c(0,0.5,0.5,1),new=TRUE)
plot(fig,main='',xlab='3')
polygon(fig,col='yellow',border='darkblue')
par(fig=c(0.5,1,0,0.5),new=TRUE)
plot(fig,main='',xlab='4')
polygon(fig,col='darkblue',border='darkred')
image.png
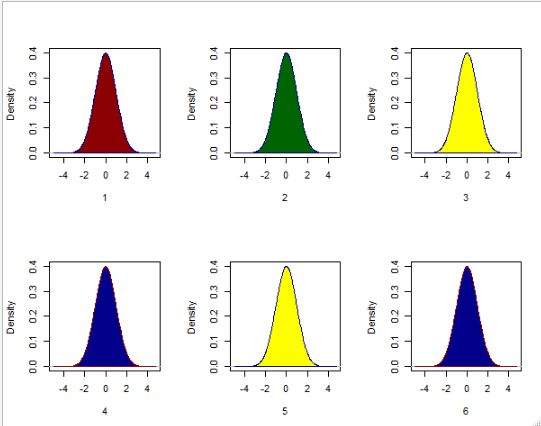
par的
mfrow或
mfcol参数，设置nrow和ncol，
mfrow表示按行对图片进行安放，
mfcol表示按列对图片进行安放；
par(mfrow=c(2,3))
fig <- density(rnorm(200000))
plot(fig,main='',xlab='1')
polygon(fig,col='darkred',border='darkblue')
plot(fig,main='',xlab='2')
polygon(fig,col='darkgreen',border='darkblue')
plot(fig,main='',xlab='3')
polygon(fig,col='yellow',border='darkblue')
plot(fig,main='',xlab='4')
polygon(fig,col='darkblue',border='darkred')
plot(fig,main='',xlab='5')
polygon(fig,col='yellow',border='darkblue')
plot(fig,main='',xlab='6')
polygon(fig,col='darkblue',border='darkred')
image.png
3.[一维]数据展示
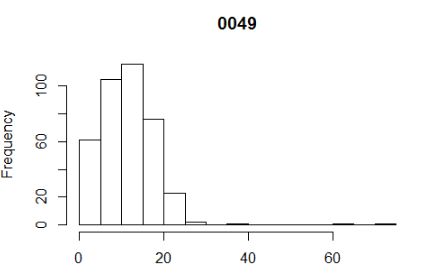
- histogram 直方图
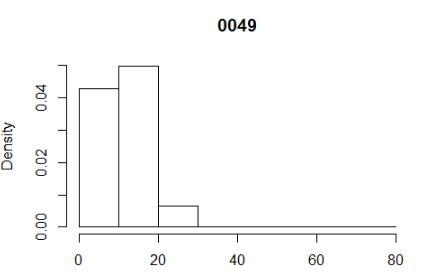
hist(e$MBases[e$plate=='0049'],breaks=12,main='0049',xlab=' ')
hist(e$MBases[e$plate=='0049'],breaks=c(0,10,20,30,40,80),main='0049',xlab=' ')
a.展示一维数据比较常用的一种方法；
b.可以设置breaks（设置分割份数和分割断点），调整数据展示；
image.png
image.png
- KDE(kernel density estimates)
核密度估计
a.KDE 用于对给定数据拟合一条光滑的曲线；
b.density相关参数：kernel可设定核函数，默认为高斯；bw即bindwidth，R文档推荐设置为‘SJ’，亦可进行其他设置；adjust默认为1，实际 bindwidth =bw*adjust；
density(x, bw = "nrd0", adjust = 1,
kernel = c("gaussian", "epanechnikov", "rectangular",
"triangular", "biweight",
"cosine", "optcosine"),
weights = NULL, window = kernel, width,
give.Rkern = FALSE,
n = 512, from, to, cut = 3, na.rm = FALSE, ...)
library(ks)
plot(kde(x)$eval.points,kde(x)$estimate, main=paste0('density: ','bw= ',round(kde(x)$h,3)),xlab='',ylab='Frequency',type="l")
Rplot03.png
1.
kde可用于对1-6维data进行核密度估计；
2.
$eval.points即用于估计的点，对应于
density中的x，对应于作图的x轴；
3.
$estimate即对应的估计值，在
$eval.points基础上产生的密度估计；
c.实际问题为估计密度函数，X=x处（即斜率）计算为
image.png
n <- 1000
x <- rnorm(n)
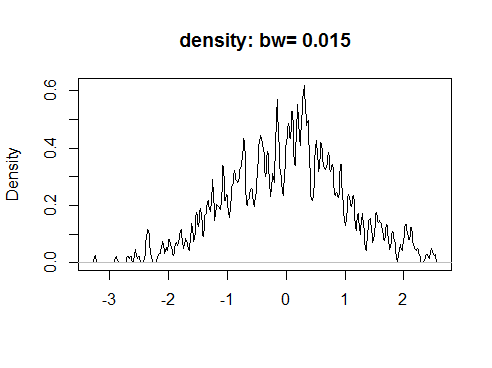
plot(density(x,bw=0.01,adjust=1.5),
main=paste0('density: ','bw= ',round(density(x,bw=0.01,adjust=1.5)$bw,3)),
xlab='')
plot(density(x,bw=0.1,adjust=1.5),main=paste0('density: ','bw= ',round(density(x,bw=0.1,adjust=1.5)$bw,3)),xlab='')
plot(density(x),
main=paste0('density: ','bw= ',round(density(x)$bw,3)),
xlab='')
Rplot.png
Rplot01.png
Rplot02.png
可以看出，随着bindwidth的增加，曲线逐渐平缓，第一感觉，bindwidth越大会越好（这个语境应该也知道，第一感觉是错的）；
下面的解释感觉hin到位：
对于给定样本量N，h选得太大，不符合h趋向于0。h选得太小，用于估计的点实际上非常少。这也就是非参数估计里面的bias-variance tradeoff：如果h太大，用于计算的点很多，可以减小方差，但是方法本质要求h→0，bias可能会比较大；如果h太小，bais小了，但是用于计算的点太少，方差又很大。所以理论上存在一个最小化mean square error的一个h。
- r|d|p|q|
在R中的分布函数，对应的一些函数的规则需要了解：
r开头，如rnorm为生成相应分布的随机数；
d开头，即density，为概率密度；
p开头，为累积概率密度；
q开头，与p相反，可以计算出相应概率下的x，即具有计算分位数的功能；
set.seed(3000)
xseq<-seq(-4,4,.01)
densities<-dnorm(xseq, 0,1)
cumulative<-pnorm(xseq, 0, 1)
randomdeviates<-rnorm(1000,0,1)
par(mfrow=c(1,3), mar=c(3,5,4,2))
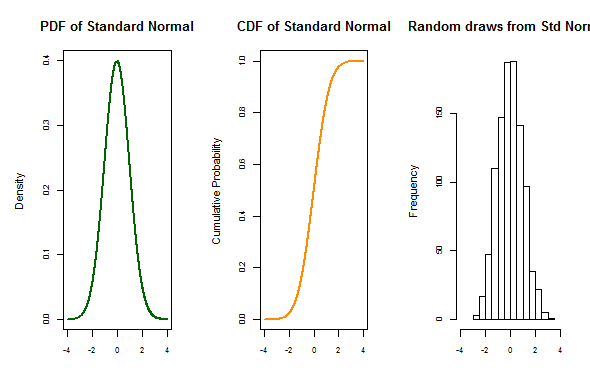
plot(xseq, densities, col="darkgreen",xlab="", ylab="Density", type="l",lwd=2, cex=2, main="PDF of Standard Normal", cex.axis=.8)
plot(xseq, cumulative, col="darkorange", xlab="", ylab="Cumulative Probability",type="l",lwd=2, cex=2, main="CDF of Standard Normal", cex.axis=.8)
hist(randomdeviates, main="Random draws from Std Normal", cex.axis=.8, xlim=c(-4,4))
这是从normal_distribution_function找到的代码，让我对这些概念的理解更加清晰了；
-
dnorm(x, mean = 0, sd = 1, log = FALSE)是指在限定条件的正态分布下，特定x的概率密度；比如下图，x=-2的时候，红点的位置对应的y； -
pnorm即（Xqnorm其实与pnorm是相反的计算过程，给定的值为累积密度值，反应在下图，即根据左下角类三角形的面积可以求得x=-2；
ugly but explain
Rplot04.png
4.Grouping -排排坐吃果果
[参考内容]
https://mathisonian.github.io/kde/
核密度估计-知乎