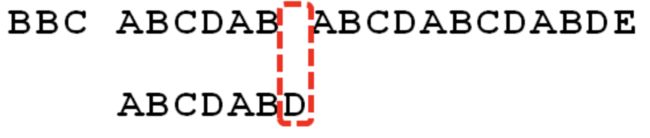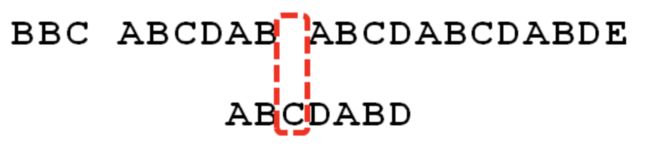一:串
串就是字符有限序列,即字符串. 3.串的顺序存储 4.串的链式存储 5.朴素模式匹配 总结自此文 2.使用最大长度表 3.引入next数组 上面是获取一个模式串的next数组的demo. 4.优化KMP算法 解决方法就是当p[j]=p[next[j]]时,不再移动next[j]位,而是next[next[j]] 使用新的next数组,next[3]=0,移动3位. next[0]=-1,i++,j++. 修改一下获取next数组的函数 贴出KMP完整的代码,是从原文复制的,具体看前面贴出来的地址,讲的非常详细. 5.KMP算法的时间复杂度
1.字符串比较大小
两个字符串s1(a1a2a3..an)和s2(b1b2b3...bm),当满足下面两个条件之一时,s1
字符串与线性表很相似.但是线性表关注单个元素的查找插入删除,字符串出了这些,还得关注字串的操作.
自然也是存在数组中,有时候会在下标0的位置存上串的长度,也有放最后的,也有的像C语言那样,在最后一个字符后面存一个"\0",这个是ASCII码的一个字符,表示串到这里结束.
字符串使用链式存储在各个方面上都不如顺序存储,经常被存在静态区,不会动态的管理,也有特殊的结构会使用链式存储,每个节点可以存1个字符,也可以存多个字符,具体看情况.
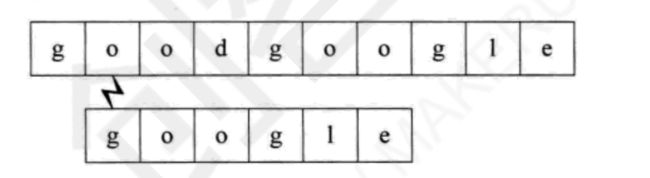
在一个字符串中搜索指定字串的位置,叫做模式匹配.
最简单的匹配思路,就是从头开始对比,遇到不一样的,就把整个字串往后移动一位,重新对比.
二:KMP模式匹配
首先定义一些概念,文本字符串S,模式字符串P,S中字符的下标为i,P中字符的下标为j.
1.最大公共元素长度
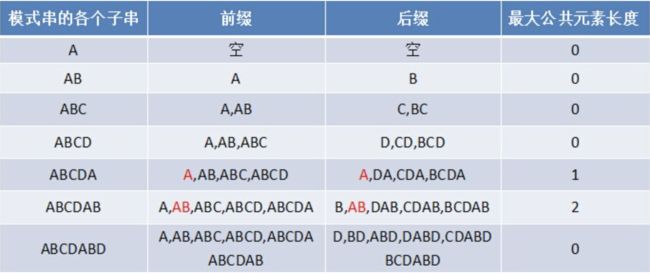
对于一个模式串ABCDABD,从左到右一位一位增加,有7种子串,A;AB;ABC...
引入两个概念叫前缀和后缀,A只有一位,没有前缀后缀;AB前缀是A,后缀是B;ABC前缀是A,AB,后缀是C,BC;ABCD的前缀是A,AB,ABC以此类推
再引入前缀后缀的最大重复长度的概念,A;AB;ABC;ABCD都没有重复,ABCDA重复长度是1;ABCDAB重复度是2;ABCDABD重复长度是0,因为前缀是A后缀是D.
使用方法:失配时,模式串向右移动的位数为:已匹配字符数 - 失配字符的上一位字符所对应的最大长度值.
i的前4位都是第一个就匹配不上,因此都是右移一位.
当S[i]=p[j]的时候,i和j都增加,也就是对比下一字符是否相同.
现在遇到第7位字符失配,那么如果是根据朴素模式匹配,则是模式串P右移一位,实际上能看出来一位肯定是没用的;
此时P应该向右移动6-2=4,因为已经匹配上了6位,这6位的最大长度是2.
又匹配两位之后,再次适配,再移动2-0=2位.
然后发现第一位就匹配不上,继续移动.
需要移动6-2=4位.
下面是刚才的最大长度表,刚才说到应用方法是(已匹配字符数 - 失配字符的上一位字符所对应的最大长度值)
也就是每次都得看j上一位的的最大长度,那为了对齐下标,干脆把这个表往右移动一位,形成数组,之后根据j去找next[j]就是需要右移的位数,这就是next数组.
右移之后把next数组的第一位填充为-1.
现在,使用方法是:失配时,模式串向右移动的位数为:失配字符所在位置 - 失配字符对应的next 值.
// 计算 arr[] 的 next 数组
public static int[] getNextArray(char[] arr) {
if (arr.length == 1) {
return new int[]{-1};
}
int[] next = new int[arr.length];
// 根据定义初始化next数组,0位置为-1,1位置为0.
next[0] = -1;
next[1] = 0;
int pos = 2; // 当前位置
int cn = 0; // 当前位置前一个字符的 next[] 值(最长相等前后缀的长度)
while (pos < next.length) {
if (arr[pos - 1] == arr[cn]) {
// 当字符串的 pos-1 位置与 pos-1 位置字符所对应的最长相同前后缀的下一个字符 arr[next[pos-1]] 相等时
// 我们就能确定 next[pos] 的值为 pos-1 位置所对应的 next[pos-1] + 1,即 ++cn.
next[pos++] = ++cn;
} else if (cn > 0) {
// 当着两个字符 不相等 时,cn向前跳跃到 next[cn] 的位置,去寻找长度更短的相同前后缀。
cn = next[cn];
} else {
// cn<=0; 此时说明前面已经没有相同前后缀了,即 cn 已经没办法再跳跃了,
// 此时 pos 对应的 next[pos] 值为 0 (无相同前后缀)
next[pos++] = 0;
}
}
return next;
}
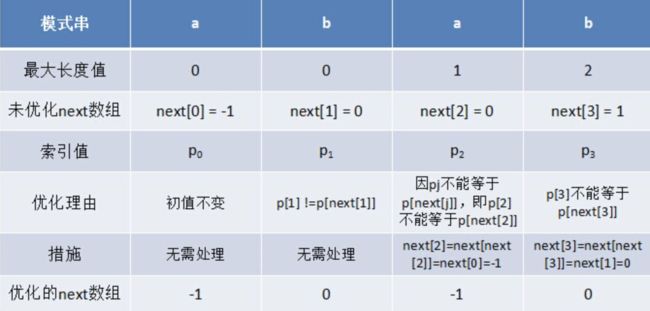
next数组仍然可以优化;
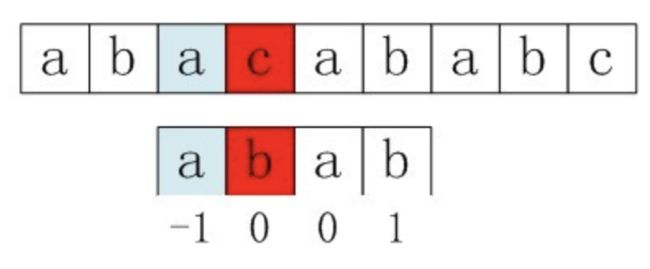
比如下面这个例子,得到next数组是-1,0,0,1;因此右移j-next[j] = 3-1=2位.
移动2位之后,这时可以看到j=1时失配,需要移动j-next[j] = 1-0=1位,但是看一眼发现移动一位也还是一样的失配,那这一步岂不是白走了,因此这里可以优化.
问题在于出现了p[j]=p[next[j]],也就是图一里的情形.
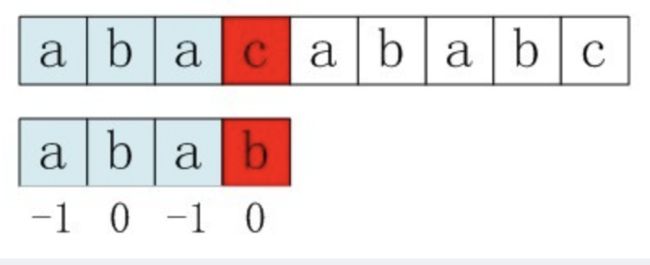
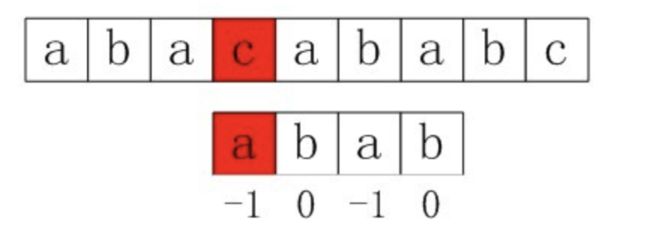
当p[j]!=s[i]时,p会右移,移动之后一定是从p[next[j]]和s[i]开始比较.从上面两张图可以就看出来,这也是KMP的核心.
因此当p[j]=p[next[j]]时,下面这一步就白走了,必然是适配的.
public static int[] next(String p) {
int[] next = new int[p.length()];
int k = -1, j = 0;
next[0] = -1; // 初值为-1
while(j < p.length() - 1) {
// p[k]表示字符串的前缀,p[j]表示字符串的后缀
if(k == -1 || p.charAt(k) == p.charAt(j)) { // 判断的先后顺序不能调换
k++;
j++;
// 后面即是求next[j+1]的过程
if(p.charAt(k) == p.charAt(j)) // 此处等价于if(p[j] == p[ next[j] ])
// 因为不能出现p[j] = p[ next[j] ],所以当出现时需要继续递归,k = next[k] = next[next[k]]
next[j] = next[k]; // 此处等价于next[j] = next[ next[j] ]
else
next[j] = k;
}
else {
k = next[k];
}
}
return next;
}
public class KMP {
public static void main(String[] args) {
String s = "abacababc";
String p = "abab";
System.out.println(Index_KMP(s, p));
}
//优化过后的next数组求法
public static int[] next(String p) {
int[] next = new int[p.length()];
int k = -1, j = 0;
next[0] = -1; // 初值为-1
while(j < p.length() - 1) {
// p[k]表示字符串的前缀,p[j]表示字符串的后缀
if(k == -1 || p.charAt(k) == p.charAt(j)) { // 判断的先后顺序不能调换
k++;
j++;
// 后面即是求next[j+1]的过程
if(p.charAt(k) == p.charAt(j)) // 此处等价于if(p[j] == p[ next[j] ])
// 因为不能出现p[j] = p[ next[j] ],所以当出现时需要继续递归,k = next[k] = next[next[k]]
next[j] = next[k]; // 此处等价于next[j] = next[ next[j] ]
else
next[j] = k;
}
else {
k = next[k];
}
}
return next;
}
public static int Index_KMP(String S, String P) {
int i = 0, j = 0;
int[] next = next(P);
while(i < S.length() && j < P.length()) {
if(j == -1 || S.charAt(i) == P.charAt(j)) { // 如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++. 注意:这里判断顺序不能调换!
i++;
j++;
}
else
// 如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j]
// next[j]即为j所对应的next值,效果为进行回溯
j = next[j];
}
if(j == P.length())
return i - j;
else
return -1;
}
}
因为不像朴素模式那样i会回溯,因此S这一层是n的复杂度,另外求next数组可以从代码上看出来,是另一个规模参数m的,因此整体复杂度是O(n+m).