承接上一篇有关如何处理数据的文章,这一篇,我们来一次实战,让大家感受一下这个过程。
Iris数据集是一个比较特别的数据集,早在1936年Ronald Fisher就将此数据集用于了数据挖掘实验。Fisher是一位非常出名的遗传统计学家,其用他所擅长的统计利器揭开了一个又一个有关生命的奥秘。
Iris数据集的地位就相当于遗传学家眼中的果蝇,其花朵的性状分明,用来学习数据挖掘再好不过。因此python的sklearn库中内置了此数据集,大家不用下载,一行代码就可以获得该数据集。
导入,清洗
因为数据规范,该数据不存在清洗的过程,导入也非常简单。
他的数据集里包含了150个个体,包含三种鸢尾花,分别是山鸢尾、变色鸢尾、维吉尼亚鸢尾。每一个个体有四个特征,分别是花萼的长宽和花瓣的长宽。同时还有标签变量target,表示了花朵的种类,用0、1、2表示。
存在csv文件中是这样的。
下面是处理数据的代码。代码中涉及了如何将花个体与标签两个表格合并的过程。
from sklearn import datasets
import matplotlib.pyplot as plt
from pandas import DataFrame
import pandas as pd
import os
path = 'C:/python/python code/scikit-learn/'
iris = datasets.load_iris()
data = iris.data
target = iris.target
data_information = DataFrame(data, columns=['bcalyx', 'scalyx', 'length', 'width'])
data_target = DataFrame(target, columns = ['target'])
data_csv = pd.concat([data_information, data_target], axis = 1)
if not os.path.exists(path):
os.makedirs(path)
filename = path + 'data.csv'
data_csv.to_csv(filename)
单变量探索
下面是单变量探索的代码。
import matplotlib.pyplot as plt
from pandas import DataFrame
import pandas as pd
def drawing(nature):
data = pd.read_csv('data.csv')
data1 = data[data['target'] == 0]
data2 = data[data['target'] == 1]
data3 = data[data['target'] == 2]
breed1_bcalyx = []
for i in data1[nature]:
breed1_bcalyx.append(i)
breed2_bcalyx = []
for i in data2[nature]:
breed2_bcalyx.append(i)
breed3_bcalyx = []
for i in data3[nature]:
breed3_bcalyx.append(i)
breed = []
breed.append(breed1_bcalyx)
breed.append(breed2_bcalyx)
breed.append(breed3_bcalyx)
pd1 = DataFrame(breed, index = ['breed1', 'breed2', 'breed3'])
pd1 = pd1.T
pd1.plot()
plt.show()
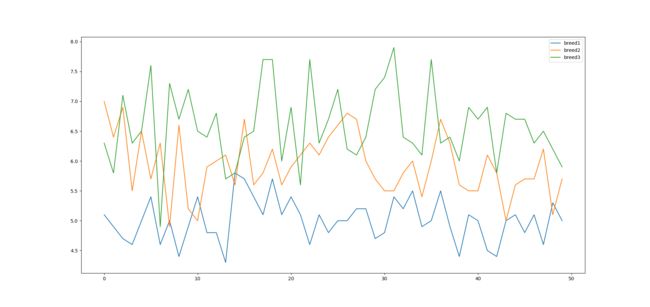
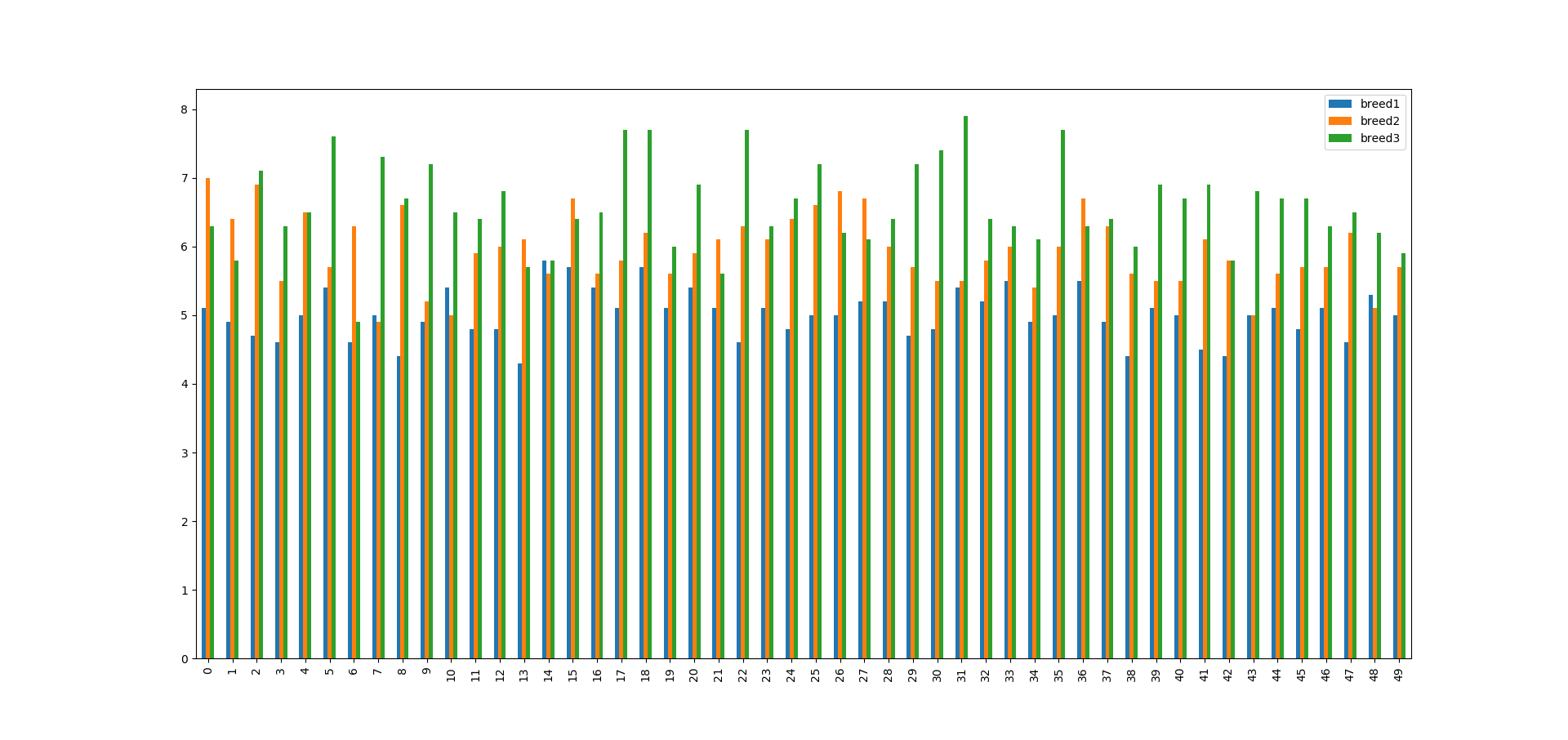
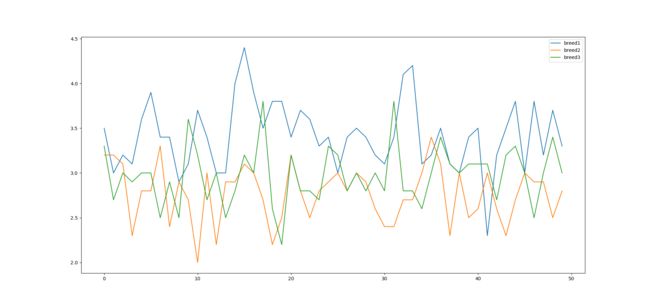
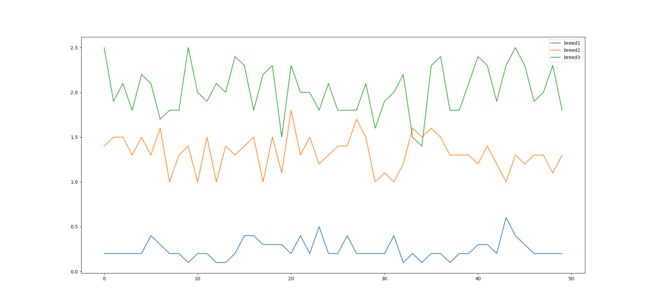
drawing('width')
从这几张图中我们就可以看出来,相比于花萼的长宽,这三种花在花瓣的长宽上差异更加明显。
多变量探索
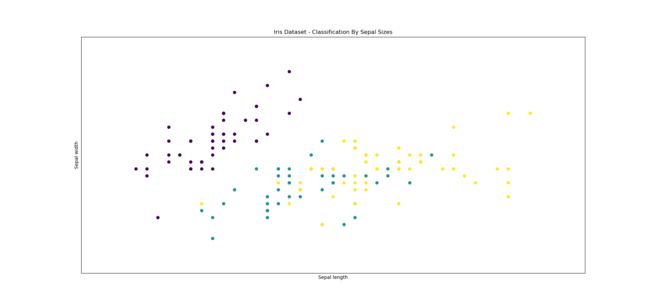
接下来我们探索并比较,花萼长宽和花瓣长宽这两组因子组合分别对花朵种类的影响。
import matplotlib.pyplot as plt
from sklearn import datasets
import matplotlib.patches as mpatches
iris = datasets.load_iris()
x = iris.data[:, 2]
y = iris.data[:, 3]
species = iris.target
x_min, x_max = x.min()-.5, x.max() + .5
y_min, y_max = y.min()-.5, y.max() + .5
plt.figure()
plt.scatter(x, y, c = species)
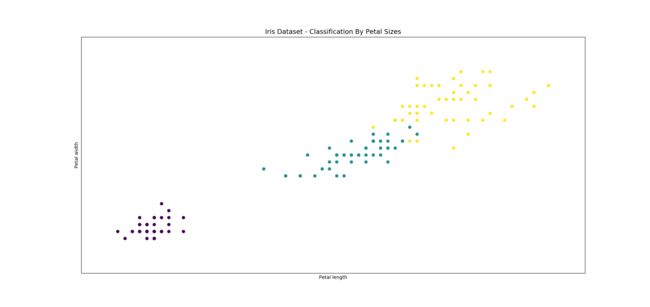
plt.title('Iris Dataset - Classification By Petal Sizes', size = 14)
plt.xlabel('Petal length')
plt.ylabel('Petal width')
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xticks(())
plt.yticks(())
plt.show()
如果说单变量探索的可视化结果还不够明显,那么多变量探索就更加说明这个问题。三种花在花瓣上的区别远远大于花萼。如果更细致的分析,在花萼宽的区别不如在花萼长上的区别。
在花萼宽的区别上后两种花性状表现几乎是互相交错的,不过这个性状表现仍然可以清晰的分出第一种与后两种花。因此我们四个因素都要用,不排除任何因子。
但是我们也发现,貌似花萼长宽之间是有相关关系的,花瓣长度也是如此。所以我们要进行降维。
import matplotlib.pyplot as plt
from sklearn import datasets
from mpl_toolkits.mplot3d import Axes3D
from sklearn.decomposition import PCA
iris = datasets.load_iris()
x_reduced = PCA(n_components = 3).fit_transform(iris.data)
species = iris.target
fig = plt.figure()
ax = Axes3D(fig)
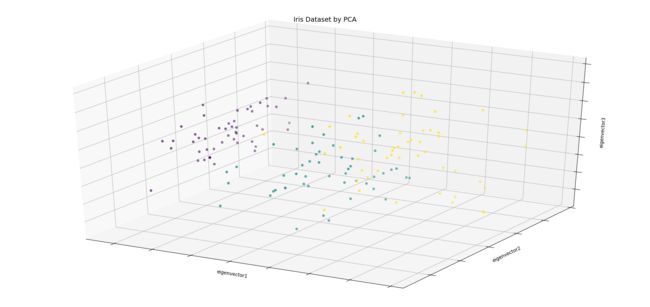
ax.set_title('Iris Dataset by PCA', size = 14)
ax.scatter(x_reduced[:, 0], x_reduced[:, 1], x_reduced[:, 2], c = species)
ax.set_xlabel('eigenvector1')
ax.set_ylabel('eigenvector2')
ax.set_zlabel('eigenvector3')
ax.w_xaxis.set_ticklabels(())
ax.w_yaxis.set_ticklabels(())
ax.w_zaxis.set_ticklabels(())
plt.show()
我们设置降维成三维,并在3D图上可以直观的感受到降维成三个解释变量后的花朵分布情况。
K-means预测
我们只有150个个体,这里我们先将数据顺序打乱,然后取前140个作为训练集,最后10个做测试集。
import numpy as np
from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
np.random.seed(0)
iris = datasets.load_iris()
x = iris.data
y = iris.target
i = np.random.permutation(len(iris.data))
x_train, y_train = x[i[:-10]], y[i[:-10]]
x_test, y_test = x[i[-10:]], y[i[-10:]]
knn = KNeighborsClassifier()
knn.fit(x_train, y_train)
y_pre_test = knn.predict(x_test)
print(y_pre_test)
print(y_test)
运行后发现,我们的识别错误率为10%。
分类情况可视化
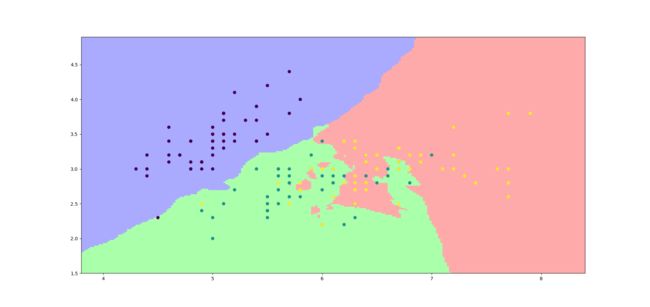
我们现在将K-means方法的分类情况用散点图可视化出来,让大家更直观的感受到算法分类结果。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
iris = datasets.load_iris()
x = iris.data[:, :2]
y = iris.target
x_min, x_max = x[:, 0].min() - .5, x[:, 0].max() + .5
y_min, y_max = x[:, 1].min() - .5, x[:, 1].max() + .5
cmap_light = ListedColormap(['#AAAAFF', '#AAFFAA', '#FFAAAA'])
h = .02
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
knn = KNeighborsClassifier()
knn.fit(x, y)
Z = knn.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.figure()
plt.pcolormesh(xx, yy, Z, cmap = cmap_light)
plt.scatter(x[:, 0], x[:, 1], c = y)
#plt.xlim(xx.min(), xx.max())
#plt.ylim(yy.min(). yy.max())
plt.show()
我们可以很容易发现。第一类花和后面两种花的分类情况是非常好的,但是后面两种花就有点难分难解了。这在我们之前的单变量和多变量分析中其实也是有体现,埋下伏笔了的。不过没办法,我们只有四个特征。
从这里也可以体现,从单变量分析与多变量分析中确定大致的分析策略也是很重要的一步。
不要只重视模型的选择,而忽略了数据的选择!