原文链接:http://tecdat.cn/?p=22862
如何使用Python通过蒙特卡洛模拟自动计算风险值(VaR)来管理投资组合或股票的金融风险。
金融和投资组合风险管理中的VaR?
VaR是 "风险价值 "的缩写,是许多公司和银行用来确定其公司内部金融风险水平的工具。风险值是为公司的投资而计算的,也可能是为检查银行或公司所管理的投资组合的风险水平。
该计算可以被认为是一种统计方法。它也可以简化为以下语句
风险值是在一定的概率水平(置信区间)下将产生的最小损失或在一定的概率水平下将实现的最大损失。
上图显示了一个公司在α%的置信水平下可能面临的最大损失。在个人层面上,VaR可以帮助你预测或分析你的投资组合可能面临的最大损失。
蒙特卡洛模拟
蒙特卡洛模型是Stanislaw Ulam和John Neumann的心血结晶,他们在第二次世界大战后开发了这个模型。该模型是以摩纳哥的一个赌博城市命名的,这是因为赌博中存在机会和随机性。
蒙特卡洛模拟是一个概率模型,它使用产生的随机变量与经济因素(期望收益率、波动率),来预测结果。该模型经常被用来计算风险和不确定性。
我们现在将使用蒙特卡洛模拟为我们的资产组合生成一组预测收益,这将有助于我们找出我们投资的风险值。
在Python中计算VaR
我们将首先通过导入所需的库和函数
#导入所有需要的库
import matplotlib.pyplot as plt
import numpy as np
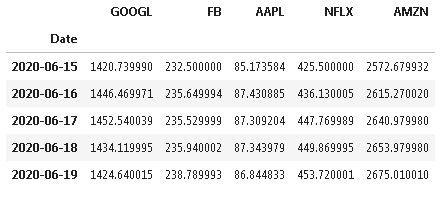
import pandas as pd为了我们项目的目的,我考虑了过去两年的 股票。
for i in range(len): web.get_data(tickers\[i\]
stocks.tail()下一步,我们将计算每个资产的组合权重。可以通过实现最大夏普比率来计算资产权重。
#年化收益率
historical_return(stocks)
#投资组合的样本方差
sample_cov#夏普比率
EffFro(mu, Sigma, weight_bounds=(0,1)) #负数的权重界限允许做空股票
max_sharpe() #可以使用增加目标来确保单个股票的最小零权重最大夏普比率的资产权重
资产权重将被用于计算投资组合的期望收益。
#VaR计算
rx2 = \[\]#换为最大夏普比率的资产权重
list(sharpe.values())现在,我们将把投资组合的股票价格转换为累计收益,这也可以被视为本项目的持有期收益(HPR)。
tick = (tick +1).cumprod()#画出所有股票的累积/HPR的图形
tick\[col\].plot()plt现在,我们将挑选出每个资产的最新HPR,并使用.dot()函数将收益率与计算出的资产权重相乘。
sigma = pre.std()
price=price.dot(sh_wt) #计算加权值在计算了投资组合的期望收益和波动率(期望收益的标准差)后,我们将设置并运行蒙特卡洛模拟。我使用的时间是1440(一天中的分钟数),模拟运行20,000次。时间步长可以根据要求改变。我使用了一个95%的置信区间。
for j in range(20000): #20000次模拟运行(rtn/Time,sigma/ sqrt(Time),Time)
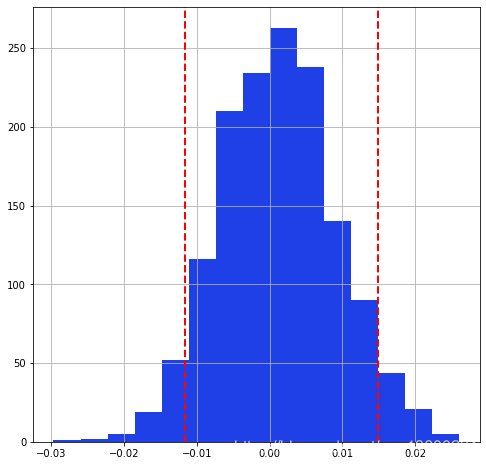
plt(np.percentile(daily_returns,5)1440分钟内一天的收益范围 | 红色 - 最小损失 | 绿色 - 最小收益
将收益率的分布图可视化,我们可以看到以下图表
plt.hist(returns)
plt.show()输出上限和下限的准确值,并假设我们的投资组合价值为1000元,我们将计算出应该保留的资金数额弥补我们的最低损失。
print(percentile( returns,5),percentile( returns,95)) VaR - 在5%的概率下,最小损失为5.7%,同样,在5%的概率下,收益可以高于15%每天的最低损失是1.29%,概率为5%。
所得金额将标志着每天弥补你的损失所需的金额。这个结果也可以解释为你的投资组合在5%的概率下将面临的最低损失。
总结
上面的方法显示了我们如何计算投资组合的风险价值(VaR)。对于使用现代投资组合理论(MPT)计算一定数量的投资组合,有助于巩固你对投资组合分析和优化的理解。最后,VaR与蒙特卡洛模拟模型配合使用,也可用于通过股价预测损失和收益。这可以通过将产生的每日收益值与各自股票的最终价格相乘来实现。
最受欢迎的见解
1.R语言基于ARMA-GARCH-VaR模型拟合和预测实证研究