IOTA 基石 - Sponge 算法详解

一、概要

    Sponge是IOTA自身抽象的 ，目前有两种实现，一个是kerl,另外一个curl。而kerl 是基于hash 散列函数Keccak 封装。而curl 自是自己法明的hash 散列函数。一方面，像区块链地址生成，交易签名的实现等，都需要依赖于此hash散列函数；另一方面，基于该类hash 签名具有防量子算法攻击的作用，导致iota 目前的 账户体系的特殊(区块链地址不可重用，后面在详细分析)，所以，有必要深入该算法实现。

二、详细介绍&解析

     IOTA 使用了三进制作为编码方式，所以使用了 SHA-3 发明者设计的三进制哈希算法 Curl；但是波士顿和 MIT 大学在 2017 年 9 月发布了一篇名为IOTA Vulnerability Report: Cryptanalysis of the Curl Hash Function Enabling Practical Signature Forgery Attacks on the IOTA Cryptocurrency的报告，指出IOTA 的签名实现中，使用 Curl 三进制哈希算法，会存在hash 碰撞。

     作为区块链项目底层的重要设施的哈希算法，Curl 并没有经历过较长时间的研究和审查就这样使用在了公链中，这种做法并不是特别的明智，在出现安全隐患之后，IOTA 团队切换至更加成熟的 Keccak 哈希算法，当然，curl 本身作为hash 摘要还是没问题的。这里额外像补充密码学中的一条『黄金法则』- 永远不要自己发明加密算法。

The golden rule of cryptographic systems is “don’t roll your own crypto.”

因此，本章节打算用4小节来详细分析
1）Sponge 算法蔟设计
2）Keccak 算法详解
3）Kerl 算法详解
4）Curl 算法详解

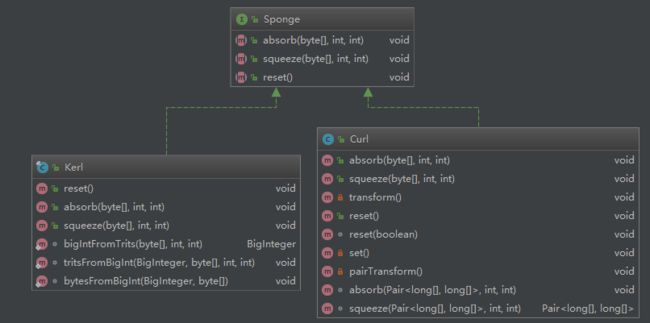
2.1 Sponge算法蔟设计

Sponge 算法蔟

    上面为IOTA 设计的海绵函数类图，主要实现有Kerl 以及 Curl。然后下面为这俩类函数在IOTA 中的用途：

Sponge 用途

    根据[Sponge 用途]总结，我们可以知道，区块链地址生成、签名生成、验签 以及 bundle hash 生成都是使用Kerl hash 算法，另外，iota 地址是81t'rytes组成，然后在用9个trytes 作为校验和；这里需要注意的是，在iota 中的bundle模型 才对应我们日常理解的transaction，而iota 中的transaction 模型 则对应比特币中input/output，这个在后续会详细分析。，
    另外Curl-P-N 中的N 则表明对一个输入运算相同的hash 转换函数N 次；transaction 模型的hash 生成 以及 bundle 中的微型 pow 使用Curl-P-81, Milestone 校验则使用Curl-P-27。

2.2 Keccak 算法详解

    在介绍Sponge 前，我们先来介绍Keccak，Keccak使用的是海绵函数:

海绵函数

它使用有限的状态，接收任何长度的输入字节数组，然后按照指定长度字节数组输出。

海绵函数是由三个部分组成：

• 一个内存状态 S，包含 b个 bit
• 一个能置换或者转换内存状态，固定大小的转换函数 f
• 一个填充函数（padding function）P

内存状态会分成两个区块，R（大小为 r bit）与 C（大小为b-r bit）。这里的参数 r又叫做转换率（bitrate），而 c叫做容量（capacity）。填充函数会在输入里面增加足够的长度，让输入的比特流长度变成 r的整数倍。因此填充过后的输入可以被切成长度为 r的数个分段。然后，海绵函数运作如下：

• S先初始化为零
• 输入经过填充函数处理
• 填充后输入的前面 r个bit会与R进行XOR运算
• S经过函数 f转换成 f(S)
• 如果填充后输入还有剩余，下一 r bit的分段与 R进行XOR运算
• S转换成f(S)
• …

这过程一直重复到所有的输入都用完为止（在海棉的譬喻里面，被函数“吸收[absorb]”了）。

现在海绵函数可以依照如下的过程输出（“挤出”[squeeze]内容）：

• 此时 R里面的数据是输出的前面 r个 bit
• 如果需要更多输出，先把 S转换成f(S)
• 此时R里面的数据是输出的下面 r个bit
• …

这过程会重复到满足输出所需要的长度为止。这里值得注意的地方是，输入绝对不会与C这部分的存储器作XOR运算，而且 C这一部分存储器也不会直接被输出。 C这一部分的存储器仅仅只和转换函数f相关。在散列里面，防止撞击攻击（Collision attack）或者原像攻击（preimage attack）是依靠 C这段存储器作到的。一般实做上 C的大小会是所希望防止等级的两倍。

    开源hash算法实现org.bouncycastle中，其海绵函数实现则对应于 KeccakDigest(implement of Keccak)。这里补充一下，sha3 的核心是进一步封装了KeccakDigest 中 absorb 以及 squeeze。我们通过一段代码来了解一下：

    // 接受任意长度的字节数组内容输入
    // 返回长度为 256字节的散列结果
    public static byte[] sha3_256(byte[] bytes) {
        Digest digest256 = new SHA3Digest(256);
        //absorb
        digest256.update(bytes, 0, bytes.length);

        //结果存放，大小为256
        byte[] result = new byte[digest256.getDigestSize()];

        // squeeze，将散列结果写入result
        digest256.doFinal(result, 0);

        return result;
    }

   //SHA3Digest 继承于 Keccak ，对hash 结果的大小进行裁剪封装
    public class SHA3Digest extends KeccakDigest {
        public SHA3Digest(int bitLength) {
            //KeccakDigest(int bitLength)
            super(checkBitLength(bitLength));
        }
    }

上述代码段是sha3_256 的封装，入参是任意长度的字节数组，返回长度为 256/8 = 32字节数组的散列结果，具体的做法是通过海绵函数Keccak所提供absorb-squeeze 来实现，当然，根据上述absorb-squeeze 可以反复调用的，具体看使用者如何来架构自身的加密体系。另外，本章节不会升入Keccak 中的absorb-squeeze的代码详细。

    而IOTA 中的Kerl hash 算法，同样也是封装了KeccakDigest(384),下面详细分析。

2.3 Kerl 算法详解

    经过上面的分析，我们了解了Keccak 算法的实现原理。一方面，我们在《IOTA基石 - 三进制系统之 Trit 和 Tryte》章节中已详细分析iota 是基于三级制构建的，而KeccakDigest 接受的输入是byte 数组，返回也是字节数组；因此，Kerl 算法核心是在将输入的三进制数组转成 byte 数组作为输入，经过Keccak的absorb-squeeze 后，把输出结果转为再次转为三进制，详细先看absorb：

    public void absorb(final byte[] trits, final int offset, final int length) {
        if (length % 243 != 0) {
            throw new RuntimeException("Illegal length: " + length);
        }
        // HASH_LENGTH = 243
        // 分段处理
        for (int pos = offset; pos < offset + length; pos += HASH_LENGTH) {
            //BYTE_HASH_LENGTH = 384/8
            //convert to bytes && update
            byte[] state = new byte[BYTE_HASH_LENGTH];
            // 最后一位设置为0？
            trits[pos + HASH_LENGTH - 1] = 0;
            bytesFromBigInt(bigIntFromTrits(trits, pos, HASH_LENGTH), state);
            // absorb
            keccak.update(state);
        }
    }

上述代码段为封装keccak的absorb的实现，核心是先通过bigIntFromTrits(...)将传进的三进制字节转bigInt,然后在通过bytesFromBigInt(...)将biguInt 转成正常的字节数组，最后在使用keccak原生的absorb 实现。当然，这里是以243大小 对trits进行分段absorb，基于iota 定义hash 大小为243。对于具体的bigIntFromTrits(...) 以及 bytesFromBigInt(...) 已在《IOTA 三进制系统之 Trit 和 Tryte》中详细分析，这里不再深入。我们接着分析squeeze(...):

    public void squeeze(final byte[] trits, final int offset, final int length) {
        if (length % 243 != 0) {
            throw new IllegalArgumentException("Illegal length: " + length);
        }
        try {
            for (int pos = offset; pos < offset + length; pos += HASH_LENGTH) {

                byte[] state = new byte[BYTE_HASH_LENGTH];
                //squeeze
                keccak.digest(state, 0, BYTE_HASH_LENGTH);

                //convert into trits
                BigInteger value = new BigInteger(state);
                tritsFromBigInt(value, trits, pos, Sponge.HASH_LENGTH);
                trits[pos + HASH_LENGTH - 1] = 0;

                //calculate hash again
                for (int i = state.length; i-- > 0; ) {
                    state[i] = (byte) (state[i] ^ 0xFF);
                }
                keccak.update(state);
            }
        } catch (DigestException e) {
            e.printStackTrace(System.err);
            throw new RuntimeException(e);
        }
    }

基于absorb 是分段处理，同理，squeeze也需要分段处理，通过keccak原生的squeeze(这里对应方法keccak.digest(state, 0, BYTE_HASH_LENGTH))对相应的243 分段获取hash摘要结果，结果是byte 字节数组，存放于临时字节数组遍历state中，然后在通过tritsFromBigInt(...)将state 转为 trits。
到这里，kerl 实现分析完毕。

2.4 Curl 算法详解

    刚刚在上文有提到，Curl hash 算法用途主要有两类，一类是生成transaction 模型的唯一hash，另外一类主要是用于pow 运行；而Curl 的pow 类运算实现已有相应PearlDiver (可理解为Curl中相应的pow 实现被移到PearlDiver 中)类实现，因此，本章节不会分析pow 相应hash 运算，会在后续的pow 实现中在详细分析，这里主要是分析生成唯一hash的转换实现。当然，这里也只是分析其工程实现，至于具体的数学论证本章节不会涉及。

    因为Curl 也是海绵函数，因此我们只需分析absorb-squeeze 即可：

//------------------------absorb
    private static final int STATE_LENGTH = 3 * HASH_LENGTH; // HASH_LENGTH = 243

    private final byte[] state;

    // 构造函数，27/81
    protected Curl(SpongeFactory.Mode mode) {
        switch(mode) {
            case CURLP27: {
                numberOfRounds = NUMBER_OF_ROUNDSP27;
            } break;
            case CURLP81: {
                numberOfRounds = NUMBER_OF_ROUNDSP81;
            } break;
            default: throw new NoSuchElementException("Only Curl-P-27 and Curl-P-81 are supported.");
        }
        state = new byte[STATE_LENGTH];
        //...
    }

    public JCurl absorb(final int[] trits) {
        return absorb(trits, 0, trits.length);
    }

    public JCurl absorb(final int[] trits, int offset, int length) {

        do {
            System.arraycopy(trits, offset, state, 0, length < HASH_LENGTH ? length : HASH_LENGTH);
            transform();
            offset += HASH_LENGTH;
        } while ((length -= HASH_LENGTH) > 0);

        return this;
    }

    public int[] squeeze(final int[] trits) {
        return squeeze(trits, 0, trits.length);
    }
//-------------------------- sqeeze
    public int[] squeeze(final int[] trits, int offset, int length) {

        do {
            System.arraycopy(state, 0, trits, offset, length < HASH_LENGTH ? length : HASH_LENGTH);
            transform();
            offset += HASH_LENGTH;
        } while ((length -= HASH_LENGTH) > 0);

        return state;
    }

从上述实现中，我们可以看到absorb以及 squeeze 实现一致，首先都是 分段处理输入，每段大小为3 * 243；然后在通过当前状态存储 字节数组 state 以及 入参trits作transform()转换。当然，absorb 流程中，将入参trits 的内容作为 state 的初始值；因此，我们继续深入transform()：

    private static final byte[] TRUTH_TABLE = {1, 0, -1, 2, 1, -1, 0, 2, -1, 1, 0};

    private final byte[] state;

    // STATE_LENGTH = 3 * 243
    private final byte[] scratchpad = new byte[STATE_LENGTH];

    private void transform() {

        int scratchpadIndex = 0;
        int prevScratchpadIndex = 0;
        // 转换轮次numberOfRounds(27/81)
        for (int round = 0; round < numberOfRounds; round++) {
             // 将没一轮次的转换结果state 全量拷贝至scratchpad
            System.arraycopy(state, 0, scratchpad, 0, STATE_LENGTH);
            for (int stateIndex = 0; stateIndex < STATE_LENGTH; stateIndex++) {
                prevScratchpadIndex = scratchpadIndex;
                if (scratchpadIndex < 365) {
                    scratchpadIndex += 364;
                } else {
                    scratchpadIndex += -365;
                }
                state[stateIndex] = TRUTH_TABLE[scratchpad[prevScratchpadIndex] + (scratchpad[scratchpadIndex] << 2) + 5];
            }
        }
    }

上面的转换算法比较简单易读，核心是反复对自身转换的结果按照同样的方式进行转换指定次数(27 或者 81 次)，第一个for 主要是控制转换轮次，并将上一次转换结果全量拷贝至辅助状态scratchpad 中(两者都是长度相同的字节数组)；第二个for 循环式执行正真的转换，根据上次转换结果scratchpad 作为参考转。

转换方式如下：

stateIndex从0到STATE_LENGTH 重新计算每一个state[stateIndex] 的数值。计算方式为TRUTH_TABLE[scratchpad[prevScratchpadIndex] + (scratchpad[scratchpadIndex] << 2) + 5] 。即根据scratchpad[prevScratchpadIndex] + (scratchpad[scratchpadIndex] << 2) + 5作为index，从TRUTH_TABLE 获取相应的整数值。scratchpadIndex 从0开始，每一次for 循环作一次变更，变更条件是如果当前scratchpadIndex值小于365,则加364，否则减365；而prevScratchpadIndex则取上一次scratchpadIndex的值。上述所使用的是(代换-置换网络)算法实现。

到这里，Sponge 算法详解 分析完毕。