高级计量经济学 2：概率论与数理统计(上)

高级计量经济学 2：概率论与数理统计(上)

此文内容为《高级计量经济学及STATA应用》的笔记，陈强老师著，高等教育出版社出版。

我只将个人会用到的知识作了笔记，并对教材较难理解的部分做了进一步阐述。为了更易于理解，我还对教材上的一些部分（包括代码和正文）做了修改。

仅供学习参考，请勿转载，侵删！

⚠️注意，本文有一定量的数学证明，为数学强迫症者准备，矩阵恐惧症患者慎入。

---

本文目录：

• 2 数学工具
  • 2.3 概率论与条件概率
    • 2.3.1 概率
    • 2.3.2 条件概率
    • 2.3.3 独立事件
    • 2.3.4 全概率公式
  • 2.4 分布与条件分布
    • 2.4.1 离散型分布
    • 2.4.2 连续型分布
    • 2.4.3 多维随机向量的概率分布
    • 2.4.4 边缘密度函数
    • 2.4.5 条件分布
  • 2.5 随机变量数字特征（标量）
    • 2.5.1 期望
    • 2.5.2 方差
    • 2.5.3 协方差与相关系数
    • 2.5.4 矩
    • 2.5.5 条件期望、条件方差
  • 2.6 随机变量数字特征（向量）*
    • 2.6.1 (向量)期望
    • 2.6.2 (向量方差)协方差矩阵
    • 2.6.3 期望和协方差矩阵的性质

---

---

2 数学工具

2.3 概率论与条件概率

2.3.1 概率

概率是大量重复实验下，事件发生的频率趋向于某个稳定值，这个值就是概率。记事件 发生的概率（probability）为：

2.3.2 条件概率

记事件出太阳为 ，则在出太阳的前提下，降雨的条件概率（conditional probability）为：

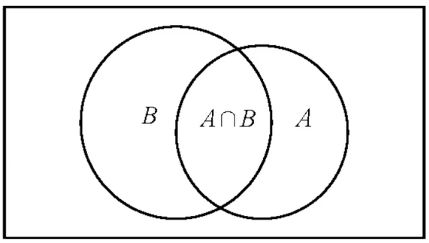
表示事件 和 同时发生，即 ，故 为“太阳雨”的概率。理解条件概率最关键的就是理解这个韦恩图：

事件 发生以后，总体就整个面积坍塌到只有 的面积，即分母缩小了。

2.3.3 独立事件

如果条件概率等于无条件概率，即 ，即 是否发生不影响 ，则说 为相互独立的随机事件，此时：

即：

这也可以作为随机变量相互独立的定义。

2.3.4 全概率公式

如果事件组 两两互不相容，但必有一件事情发生。则对任意的事件 ，一定有：

全概率事件把这个世界上的某个事件 分成 种可能性，再把事件 的条件概率按加权平均的方式汇总起来，成为无条件概率。也就是说， 发生的概率应该等于 所有可能发生的情况时 发生的概率（条件概率）的加权平均

---

2.4 分布与条件分布

2.4.1 离散型概率分布

假设随机变量 的可能取值为 ， 其对应的概率为 ，即满足 ，就称 为离散型随机变量，其分布律可以表示为：

其中， 。常见的离散分布有两点分布（Bernoulli）、二项分布（ Binomial）、泊松分布（Poisson）等。

2.4.2 连续型概率分布

如果连续型随机变量 可以取任意实数，其概率密度函数（Probability density function，pdf） 满足：

• 落入区间 的概率为

也就是说，在一维情况下，概率就是概率密度函数下的面积：

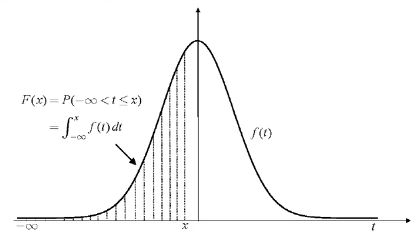
同时可以定义累计分布函数（cumulative distribution function，pdf）：

其中， 为积分变量。 度量的是从 到 为止，概率密度函数 曲线下的面积：

2.4.3 多维随机向量的概率分布

为研究变量的关系，常常同时考虑两个或多个随机变量，即随机向量（random vector）。二维连续型随机向量 的联合密度函数（joint pdf） 满足：

• 落入平面某区域 的概率为

二维随机向量的联合密度的联合密度就像是一定草帽，落入平面某区域 的概率就是此草帽下在区域 上的体积：

维连续型随机向量 可由联合密度函数 来描述。

类似的，可以定义二维随机向量 的累积分布函数为：

2.4.4 边缘密度函数

从二维联合密度 ，可计算 的一维边缘密度函数（marginal pdf）：

即给定 ，把所有 取值的可能性都加总起来（积分的本质就是加总），这样 就被积分掉了，而这个联合密度变成了只关于 的函数。

2.4.5 条件分布

条件分布函数（conditional distribution）的概念对于计量至关重要。

考虑在 条件下 的分布，记为 或 。对于连续分布，此条件相当于在草帽上 的位置垂直地切一刀所得的截面。

可以证明，条件密度函数为：

直观上，与全概率公式 十分类似。

---

2.5 随机变量的数字特征（标量）

如果我们要了解一个随机变量的分布情况，知道分布函数固然最好。但更多的时候我们并不需要知道完整的分布函数，因为某些分布函数其实只需要几个量甚至一个量就足矣描述了，比如正态分布，只需要知道 就可以确定一个分布了。这样的参数是我们感兴趣的，即所谓的数字特征。

2.5.1 期望

定义1：对于分布律为 的离散型随机变量 ，其期望（expectation）为：

期望值的直观含义就是对 进行加权平均，而权重为概率 。

定义2：对于概率密度函数为 的连续型随机变量 ，其期望为：

经济学上积分一般都可以当成是简单的求和，上式本质上也是加权平均。 成为期望算子，满足线性性：

2.5.2 方差

定义3：随机变量 的方差（variance）为：

方差衡量了随机变量的波动幅度。方差的平方根成为标准差（standard deviation），记为 。在计算方差时，常利用以下简便公式：

证明：

考虑到 是一个常数，使用线性性（见2.5.1）：

证毕。

可以看出，方差其实是期望的特例，是以自变量为 的期望，即偏离期望的期望。

2.5.3 协方差、相关系数

常常需要考虑两个变量之间的相关性，即一个随机变量会对另外一个随机变量的取值会造成影响。

定义4：随机变量 与 的协方差（covariance）为：

直观上：

• 如果 偏离其期望 为正的时候， 的偏离也为正，那么
• 如果 偏离其期望 为正的时候， 的偏离缺为负，那么

所以 一定程度上度量了 和 的关系。

计算协方差时，常用下面的简便公式：

证明：

证毕。

直观上，上面的公式与方差（2.5.2）公式非常类似。同时可以证明，协方差的运算满足线性性：

证明：

证毕。

虽然协方差也可以衡量两个随机变量的相关性，但毕竟它受 的单位影响。比如 GDP 用”元“还是”十亿元“计量，会对 造成影响的。为了统一量纲，需要用一个东西给他标准化咯。

前面提到，计量经济学中的标准化一般使用方差进行，所以这里我们定义一个相关系数，为：

可以证明，相关系数一定介于 到 之间，即 。下面给出一个绝妙的证明：

证明：

为了创造 和 、 ，我们构造一个函数：

展开这个2次方，有：

使用期望算子的线性性，并注意到 、 、 ，有：

考虑到 的统计意义是某个非负随机变量的的期望故 ，即二次函数的判别式 ：

显然，

证毕。

2.5.4 矩

如果以上提到的各定义中的积分不收敛（比如自由度为 的 分布，没有期望和方差），那么就需要找到一个更加一般的数字特征，即各阶矩（moment）

定义5： 一阶原点矩为 ，另外的 阶原点矩为

定义6： 二阶中心矩为 ， 阶中心矩为

其中，有几个矩是比较重要的：

• 一阶原点矩 实际上就是期望，表示随机变量的平均值
• 二阶中心矩 实际上就是方差，表示随机变量的波动程度
• 三阶中心矩 实际上表示的是密度函数的不对称性
• 四阶中心矩 实际上便是的是密度函数在最高处有多“尖”、在尾部有多“厚”

可以看出，三、四阶矩也对密度函数的特征有一定的描述作用。可是，三、四阶矩受随机变量 的量纲的影响。按照计量经济学的惯例，对于任何取决于单位的变量，标准化的手段是除以方差（对高维度随机变量，则是除以协方差矩阵），那么就有：

定义7：随机变量 的偏度（skewness）为

定义8：随机变量 的峰度（kurtosis）为

某个随机变量的峰度如果比较大，那么密度函数在两侧更“厚“（这就是所谓的胖尾（fat tail）），从而更加可能取尾部的极端值（outlier）

对于正态分布，峰度为3（计算出来的，不服可算），偏度为0（奇函数的三次方积分为0）。从而对任意一个随机变量 ，可以计算它与正态分布差多少，可以以此判断这个分布是否为正态分布：

定义9：随机变量 的超额峰度（excess kurtosis）为

刚一般地，对于随机变量 与任意函数 ，称随机变量函数 的期望 为矩（moment）

2.5.5 条件期望、条件方差

定义10：条件期望（condition expectation）就是条件分布 的期望，即：

（上式的最后一个等号见2.4.5 条件分布）由于 已经被积分掉，所以 只是关于 的函数。

定义 11：条件方差（condition variance）就是条件分布 的方差，即：

由于 已经被积分掉，所以 只是关于 的函数。

---

2.6 随机变量的数字特征（向量）

2.5节介绍了标量随机变量的数字特征。我们在计量上其实更多地是使用高维度的“数字”，比如：

在2.5节，随机变量 是 一个标量，比如某一年的数学成绩

实际计量中，比如要做回归时，我们往往需要用到很多年的信息：

那么这个 个随机变量 实际上构成了一个随机向量，记为

在以后， 是一个随机标量， 是随机向量， 是随机矩阵

所以，研究向量的数字特征也十分重要。所幸，向量只是标量的拓展，很多性质和公式都是有共性的。

2.6.1 向量的期望

定义1：设 为 维向量，代表 个观测值，则其期望为

2.6.2 向量的方差：协方差矩阵

协方差矩阵就是标量中的方差的概念。

定义2：设 为 维向量，代表 个观测值，则其协方差矩阵（covariance matrix）为一个 的对称矩阵：

之所以叫协方差矩阵，是因为这就是由协方差构成的矩阵。对角线上的方差其实是协方差的特例罢了。

2.6.3 (向量)期望和协方差矩阵的性质*

假设 为 常数矩阵，那么有：

• 性质1： ：期望的线性性
• 性质2： ：一维公式的推广
• 性质3： ：夹心估计量（重要！）

这些性质是可以证明的，最简单的想法就是把他们直接展开写成标量的形式。

证明1：
假设 为 常数矩阵， 为 随机向量，那么：

从而，根据定义1，有：

根据标量期望算子线性性，有：

将求和的系数部分剥离：

于是再用一次定义1：

证毕。

实际上，如果 可以是向量，那么 也可以是行数为 的任意矩阵，我证过，这不难，读者可以自己试一下。类似的，也应该有 ，我没有仔细证明它（主要是懒），但是通过它可以推出性质3。我的理解是， 既然是一个常数矩阵，那么在求期望算子作为一种针对随机变量的算子，应该对常数不起作用的。

证明2：

前面知道：

而：

且：

显然，

根据 2.5.2 和 2.5.3 有：

也就是：

证毕。

证明3：

由于：

所以：

注意到 是常数矩阵，根据线性性，可以剥离，则有：

证毕。