声明:文中所述股票仅为分析举例之用,请独立作出投资决策。Quantopian 为免费分析平台,与本文无利益关系。
如果你有买股票,尤其是美股股票,今年不太可能没注意到特斯拉TSLA。特斯拉股票今年从低点涨了将近10倍,近两天股价大幅度回调,那么你应该去买进么?
如果你是“信仰投资者”, 认定了一龙马教主的神功,那么就不必往下看了,闭着眼买然后把炒股软件删掉。 我长期也是看好特斯拉的,但是凯恩斯大师说过:“长期来看,我们都死了。。。”, 所以短期还是要尽可能分析一下。本文试图从持仓风险分析的角度来探讨下要不要买进TSLA, 所用量化分析平台为Quantopian,所用语言为Python
关于持仓风险,你大概听过最基本的是要多买一些股票,不要把鸡蛋放在一个篮子里,但是随便多买几只就可以降低风险了么? 也不然,还是要想办法量化这个风险。有一种比较简单的分析方法,就是算一下现有持仓股票的协方差. 这个数值越高,表示你所持仓的股票其实价格走势越是类似, 这在持仓总回报上来讲如果上涨会涨的很高,但是下跌也会跌的很惨,就是所谓的波动率很大。我们显然不希望大的波动率,想象一下,你的持仓今天下跌10%明天上涨10%你是否还能睡好,可能早早就抛掉了,这就可能就会浪费很多机会。
原始持仓
假设你现在持仓是美股四大神兽['FB', 'GOOG', 'AMZN', 'AAPL'],每只股票持仓比例是均等的
所以我们有持仓列表以及持股比例如下
universe = ['FB', 'GOOG', 'AMZN', 'AAPL']
weights = np.array([0.25, 0.25, 0.25, 0.25])
通过Quantopian获得这些股票过去一年的价格时间序列,并且将其正规化(Normalize)到(0,1)区间
prices = get_pricing(universe, fields='price', start_date=start, end_date=end)
normal_prices = (prices-prices.min())/(prices.max()-prices.min())
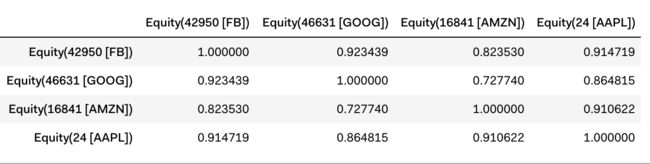
接下来利用Pandas 提供的计算covariance_matrix的方法.corr()即可以获得当前持仓的协方差矩阵cov_matrix
这些数值从0到1, 数值越大表明两支股票走势越是相关,可以看到这几支股票相关性还是很高的(大部分>0.8)
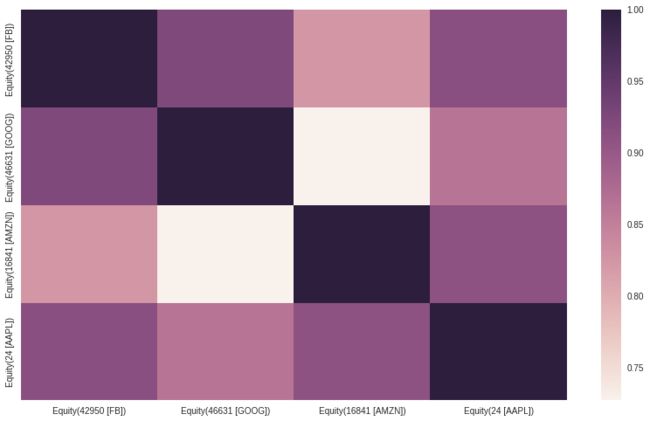
我们也可以绘制这个矩阵的热力图,利用seaborn 的.heatmap()方法
sns.heatmap(cov,xticklabels=cov.columns,yticklabels=cov.columns)
这样就可以根据颜色深浅直观的看到两支股票的相关性。
我们也可以计算持仓总体方差
total_variance = np.dot(np.dot(weights, cov_matrix.values), weights.T)
计算得到数值为 0.895608093887
原始持仓+TSLA
下面我们看下如果这个持仓我们加入了TSLA会有什么变化
现在的持仓列表以及权重分别为
universe_T = ['FB', 'GOOG', 'AMZN', 'AAPL', 'TSLA']
weights_T = np.array([0.2, 0.2, 0.2, 0.2, 0.2])
同样计算方式可得,协方差矩阵
热力图
总体方差 0.895463150009
可以看到TSLA跟其他四支股票,尤其是AMZN,AAPL相关性非常高,总体的方差同之前持仓基本一致,在比较高的水平。那么面临是否要买特斯拉,你可能要问一下自己这个问题,首先,你是否要继续增加已经比较高的持仓风险水平。如果答案是肯定的,你就是非常看好,那么好消息是增加了特斯拉并没有大幅提高整体的风险,当然前提是根据过去一年表现来看。
原始持仓+BRK.B
作为对比,我们也可以分析一下,如果增加的不是TSLA而是股神的BRK.B 会有什么结果,此时的持仓列表和权重将会是
universe_B = ['FB', 'GOOG', 'AMZN', 'AAPL', 'BRK.B']
weights_B = np.array([0.2, 0.2, 0.2, 0.2, 0.2])
我们可以得到协方差矩阵
热力图
可以看到BRK.B与其他四支股票走势有较大区别,这也符合我们的直觉,但是巴菲特也投资了很多苹果股票啊,怎么这里并没有看到很高的相关性呢,是不是可以思考一下。。
总方差计算为0.601009311705, 相对之前有大幅下降
可见如果加入了BRK.B 是会大幅降低我们当前的持仓风险,但是是否就是意味着我们要买进BRK.B 而不是特斯拉呢,这又到了投资永恒的话题,风险和收益是正相关的,承担多少风险就会有可能有多大的收益(或亏损)。但是用一些简单的量化方法来分析至少让你心中有数,不会盲目的投奔于风险之中而不自知。
本文代码
https://github.com/niuguy/blog/blob/master/ofeng/source/codes/cov-analysis.ipynb
参考文献
https://www.quantopian.com/lectures/linear-correlation-analysis
https://www.quantopian.com/lectures/position-concentration-risk