深度神经网络的特征引导黑盒安全测试(Feature-Guided Black-Box Safety Testing of Deep Neural Networks)
作者:Matthew Wicker, Xiaowei Huang, and Marta Kwiatkowska
单位:佐治亚大学,利物浦大学,牛津大学
目录
-
- 摘要
- 预备知识
- 基于人类感知的操作安全性
- 蒙特卡罗树搜索渐近最优策略
- 实验结果
- 总结
摘要
大多数现有的生成对抗样本的方法都需要一些自己使用的神经网络知识(结构、参数等)。本文以图像分类器为研究对象,提出了一种特征引导的黑盒方法,可以在不需要这种知识的情况下来验证深度神经网络的安全性。我们将生成对抗样本的过程公式化为一个两人轮流随机游戏,其中第一个玩家的目标是通过操纵特征来最小化与对抗样本的距离,第二个玩家可以是合作的、对抗的或随机的。我们证明了,理论上,两人博弈可以收敛到最优策略,并且最优策略代表了一个全局最小的对抗图像。使用蒙特卡洛树搜索,我们穷尽搜索游戏状态空间来搜索对抗样本。最后,我们展示了我们的方法如何用于评估神经网络在安全关键应用中的鲁棒性,例如自动驾驶汽车中的交通标志识别。
预备知识
设 N N N是一个有 C C C个分类的神经网络,给定一个输入 α \alpha α和一个分类 c ∈ C c\in C c∈C,我们用 N ( α , c ) N(\alpha,c) N(α,c)来表示 N N N把 α \alpha α分类为 c c c的置信度。此外,我们用 N ( α ) = a r g m a x c ∈ C N ( α , c ) N(\alpha)=arg\ max_{c\in C}N(\alpha,c) N(α)=arg maxc∈CN(α,c)来表示 N N N对 α \alpha α的分类。对于我们讨论的图像分类网络,输入域 D D D是一个向量空间。
用于计算图像间距离的度量标准通常包括 L 0 , L 1 , L 2 , L ∞ L_0,L_1,L_2,L_\infin L0,L1,L2,L∞范数等。在之后的讨论中,我们定义 ∣ ∣ α 1 − α 2 ∣ ∣ k ( k ≥ 0 ) ||\alpha_1-\alpha_2||_k(k\ge0) ∣∣α1−α2∣∣k(k≥0)为在 L k L_k Lk范数下 α 1 \alpha_1 α1和 α 2 \alpha_2 α2之间的距离。给定图像 α \alpha α,距离度量标准 L k L_k Lk,以及距离 d d d,我们定义 η ( α , k , d ) = { α ′ ∣ ∣ ∣ α ′ − α ∣ ∣ k ≤ d } \eta(\alpha,k,d)=\{\alpha'|\ ||\alpha'-\alpha||_k\le d\} η(α,k,d)={ α′∣ ∣∣α′−α∣∣k≤d}为在 L k L_k Lk范数下到 α \alpha α的距离不大于 d d d的点的集合。
定义1:给定一个输入 x ∈ D x\in D x∈D,一个 k ≥ 0 k\ge0 k≥0的距离度量标准 L k L_k Lk和一个距离 d d d,一个 c ≠ N ( α ) c\ne N(\alpha) c=N(α)的对抗样本 α ′ \alpha' α′定义为 α ′ ∈ η ( α , k , d ) , N ( α ′ ) ≠ N ( α ) , N ( α ′ ) = c \alpha'\in \eta(\alpha,k,d),N(\alpha')\ne N(\alpha),N(\alpha')=c α′∈η(α,k,d),N(α′)=N(α),N(α′)=c
a d v N , k , d ( α , c ) adv_{N,k,d}(\alpha,c) advN,k,d(α,c): c c c类别的一系列对抗样本
a d v N , k , d ( α ) = ⋃ c ∈ C , c ≠ N ( α ) a d v N , k , d ( α , c ) adv_{N,k,d}(\alpha)=\bigcup_{c\in C,c\ne N(\alpha)}adv_{N,k,d}(\alpha,c) advN,k,d(α)=⋃c∈C,c=N(α)advN,k,d(α,c):所有类别的对抗样本
a d v N , k , d ( α , c ) = ∅ adv_{N,k,d}(\alpha,c)=\empty advN,k,d(α,c)=∅: c c c类的目标安全性
a d v N , k , d ( α ) = ∅ adv_{N,k,d}(\alpha)=\empty advN,k,d(α)=∅:非目标安全性
特征提取:尺度不变特征变换(SIFT,Scale Invariant Feature Transform)算法,这是一种无需使用神经网络就可以进行对象定位和跟踪的方法。通常分为以下几个步骤:尺度空间极值检测(检测图像中相对较暗或较亮的区域)、关键点定位(确定这些区域的确切位置)和关键点描述符分配(理解图像的上下文)。
人类对图像或物体的感知可以合理地表示为一组不同大小和不同响应强度的特征(在SIFT中称为关键点)。设 Λ ( α ) \Lambda(\alpha) Λ(α)是图像的一组特征,其中每个特征 λ ∈ Λ ( α ) \lambda\in \Lambda(\alpha) λ∈Λ(α)是一个元组 ( λ x , λ y , λ s , λ r ) (\lambda_x,\lambda_y,\lambda_s,\lambda_r) (λx,λy,λs,λr), ( λ x , λ y ) (\lambda_x,\lambda_y) (λx,λy)是特征坐标, λ s \lambda_s λs是特征大小, λ r \lambda_r λr是特征的响应强度。
高斯混合模型:给定图像 α \alpha α及其关键点集合 Λ ( α ) \Lambda(\alpha) Λ(α),我们为 λ ∈ Λ ( α ) \lambda\in \Lambda(\alpha) λ∈Λ(α)定义二维高斯分布 G i G_i Gi,对于像素 ( p x , p y ) (p_x,p_y) (px,py)有:
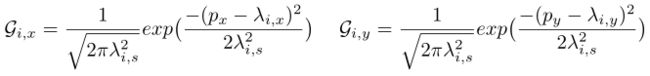
高斯混合模型就是加权计算(定义一组权重 Φ = { Φ i } i ∈ { 1 , 2 , . . . , k } \Phi=\{\Phi_i\}_{i\in \{1,2,...,k\}} Φ={ Φi}i∈{ 1,2,...,k}):
![]()
有模型之后就可以将一张图片变成高斯混合模型处理后的图片。

像素操作:定义用于操作图像的操作。
α ( x , y , z ) \alpha(x,y,z) α(x,y,z):图像 α \alpha α上位于(x,y)的像素的z通道值(通常为RGB或灰度值,RGB3个,灰度1个);
I = { + , − } I=\{+,−\} I={ +,−}是一组操作指令, τ \tau τ是表示操作幅度的正实数;
对于所有的像素(x,y)和所有的通道z∈{1,2,3},在其输入子集X上的像素操作 δ X , i : D → D \delta_{X,i}:D\rightarrow D δX,i:D→D定义为:
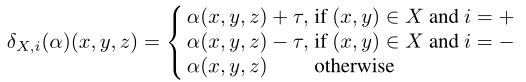
基于人类感知的操作安全性
提出了一种特征引导的方法,它不是使用梯度方向作为优化的指导,而是依赖于人类感知能力识别的目标和操作图像特征。
基于游戏的方法:
假定有两个玩家 I I I和 I I II II。玩家 I I I选择特征,而玩家 I I II II然后选择选定特征中的像素和操作指令。
尽管玩家 I I I的目标是最大程度地减少与对抗样本的距离,但玩家 I I II II可以根据高斯混合模型对像素进行采样,可以是合作者,对抗者或随机的。
我们根据 L k L_k Lk范数定义目标函数,并将与一个对抗样本的距离视为衡量其严重性的指标。
定义2:在集合 a d v N , k , d ( α , c ) adv_{N,k,d}(\alpha,c) advN,k,d(α,c)(或者 a d v N , k , d ( α ) adv_{N,k,d}(\alpha) advN,k,d(α))中找到距原始图像 α \alpha α最小距离的 α ′ \alpha' α′,定义如下:
a r g m i n α ′ { s e v α ( α ′ ) ∣ α ′ ∈ a d v N , k , d ( α , c ) ( o r a d v N , k , d ( α ) ) } \mathop{arg\ min}_{\alpha'}\{sev_\alpha(\alpha')\ |\ \alpha'\in adv_{N,k,d}(\alpha,c)(or\ adv_{N,k,d}(\alpha))\} arg minα′{ sevα(α′) ∣ α′∈advN,k,d(α,c)(or advN,k,d(α))}
其中的 s e v α ( α ′ ) = ∣ ∣ α − α ′ ∣ ∣ k sev_\alpha(\alpha')=||\alpha-\alpha'||_k sevα(α′)=∣∣α−α′∣∣k,是对抗样例 α ′ \alpha' α′对原始图像 α \alpha α的严重程度。对于N张图片,直接求平均值就是该用例最终的严重程度,距离越小,代表该反例越好。
将对抗样本的生成过程转化为一个有两个玩家 I I I和 I I II II的双人回合制游戏:
设 M ( α , p , d ) = ( S ∪ ( S × Λ ( α ) ) , s 0 , { T a } α ∈ { I , I I } , L ) M(\alpha,p,d)=(S\cup(S\times\Lambda(\alpha)),s_0,\{T_a\}_{\alpha\in\{I,II\}},L) M(α,p,d)=(S∪(S×Λ(α)),s0,{ Ta}α∈{ I,II},L)为一个游戏模型
S S S是属于玩家 I I I的一组游戏状态,每个状态代表 η ( α , k , d ) \eta(\alpha,k,d) η(α,k,d)中的一个图像
S × Λ ( α ) S\times\Lambda(\alpha) S×Λ(α)是属于玩家 I I II II的一组游戏状态,其中 Λ ( α ) \Lambda(\alpha) Λ(α)是图像的一组特征
α ( s ) \alpha(s) α(s)表示与状态 s ∈ S s\in S s∈S相关的图像, s 0 ∈ S s_0\in S s0∈S是初始游戏状态, α ( s 0 ) \alpha(s_0) α(s0)是原始图像 α \alpha α
过度关系 T I : S × Λ ( α ) → S × Λ ( α ) T_I:S\times\Lambda(\alpha)\to S\times\Lambda(\alpha) TI:S×Λ(α)→S×Λ(α)被定义为 T I ( s , λ ) = ( s , λ ) T_I(s,\lambda)=(s,\lambda) TI(s,λ)=(s,λ)
过度关系 T I I : ( S × Λ ( α ) ) × P ( P 0 ) × I → S T_{II}:(S\times\Lambda(\alpha))\times P(P_0)\times I\to S TII:(S×Λ(α))×P(P0)×I→S被定义为 T I I ( ( s , λ ) , X , i ) = δ X , i ( α ( s ) ) T_{II}((s,\lambda),X,i)=\delta_{X,i}(\alpha(s)) TII((s,λ),X,i)=δX,i(α(s)),其中 δ X , i \delta_{X,i} δX,i是像素操作
在每一个游戏状态 s ∈ S s\in S s∈S上,玩家 I I I都会选择一个关键点 λ \lambda λ,玩家 I I II II会选择一个对 ( X , i ) (X,i) (X,i),其中 X X X是一组输入维度, i i i是一个操作指令
标记函数 L : S ∪ ( S × Λ ( α ) ) → C × G L:S\cup(S\times\Lambda(\alpha))\to C\times G L:S∪(S×Λ(α))→C×G给每一个状态 s s s或 ( s , λ ) (s,\lambda) (s,λ)分配一个类别 N ( α ( s ) ) N(\alpha(s)) N(α(s))和一个二维高斯混合模型 G ( Λ ( α ( s ) ) ) G(\Lambda(\alpha(s))) G(Λ(α(s)))
游戏模型路径:
游戏模型的路径是游戏状态的序列 s 1 u 1 s 2 u 2 . . . s_1u_1s_2u_2... s1u1s2u2...,使得对于所有 k ≥ 1 k\ge1 k≥1,对于某些特征 λ k \lambda_k λk,有 u k = T I ( s k , λ k ) u_k=T_I(s_k,\lambda_k) uk=TI(sk,λk);对于某些 ( X k , i k ) (X_k,i_k) (Xk,ik),有 s k + 1 = T I I ( ( s k , λ k ) , X k , i k ) s_{k+1}=T_{II}((s_k,\lambda_k),X_k,i_k) sk+1=TII((sk,λk),Xk,ik)
令 l a s t ( p ) last(p) last(p)为有限路径 p p p的最后状态, P a t h a F Path_a^F PathaF是有限路径的集合,以使 l a s t ( p ) last(p) last(p)属于玩家 a ∈ { I , I I } a\in \{I,II\} a∈{ I,II}
玩家 I I I的随机策略 σ I \sigma_I σI: P a t h I F → D ( Λ ( α ) ) Path_I^F\to D(\Lambda(\alpha)) PathIF→D(Λ(α))
玩家 I I II II的随机策略 σ I I \sigma_{II} σII: P a t h I I F → D ( P ( P 0 ) × I ) Path_{II}^F\to D(P(P_0)\times I) PathIIF→D(P(P0)×I)
σ = ( σ I , σ I I ) \sigma=(\sigma_I,\sigma_{II}) σ=(σI,σII)为策略配置文件
奖励函数:
为 σ = ( σ I , σ I I ) \sigma=(\sigma_I,\sigma_{II}) σ=(σI,σII)和有限路径 p ∈ ⋃ a ∈ { I , I I } P a t h a F p\in\bigcup_{a\in \{I,II\}}Path_a^F p∈⋃a∈{ I,II}PathaF定义奖励 R ( σ , p ) R(\sigma,p) R(σ,p)。
α p ′ = α ( l a s t ( p ) ) \alpha_p'=\alpha(last(p)) αp′=α(last(p))是与路径ρ的最后状态关联的图像。
t ( p ) : N ( α p ′ ) = c ∨ ∣ ∣ α p ′ − α ∣ ∣ k > d t(p): N(\alpha_p')=c\vee || \alpha_p' - \alpha||_k>d t(p):N(αp′)=c∨∣∣αp′−α∣∣k>d表示路径已经达到一个状态,其关联图像或者在目标类c中,或者位于区域 η ( α , k , d ) \eta(\alpha,k,d) η(α,k,d)之外。只要满足 t ( p ) t(p) t(p),路径 p p p就可以终止。
奖励函数 R ( σ , p ) R(\sigma,p) R(σ,p)定义如下:
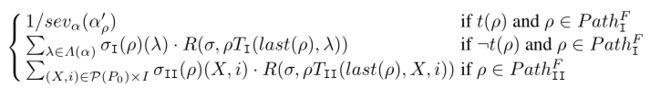
其中 σ I ( p ) ( λ ) \sigma_I(p)(\lambda) σI(p)(λ)是玩家 I I I在 p p p上选择 λ \lambda λ的概率, σ I I ( p ) ( X , i ) \sigma_{II}(p)(X,i) σII(p)(X,i)是玩家 I I II II在 p p p上选择 ( X , i ) (X,i) (X,i)的概率,路径仅终止于玩家 I I I的状态。
定义3:游戏的目的是让玩家 I I I根据玩家 I I II II的策略 σ I I \sigma_{II} σII选择一个策略 σ I \sigma_I σI,以最大化初始状态 s 0 s_0 s0的奖励 R ( ( σ I , σ I I ) , s 0 ) R((\sigma_I,\sigma_{II}),s_0) R((σI,σII),s0),即:
a r g m a x σ I o p t σ I I R ( ( σ I , σ I I ) , s 0 ) \mathop{arg\ max}_{\sigma_I}opt_{\sigma_{II}}R((\sigma_I,\sigma_{II}),s_0) arg maxσIoptσIIR((σI,σII),s0)
其中 o p t σ I I opt_{\sigma_{II}} optσII可以是 m a x σ I I , m i n σ I I max_{\sigma_{II}},min_{\sigma_{II}} maxσII,minσII或 n a t σ I I nat_{\sigma_{II}} natσII,根据该选项,玩家 I I II II充当合作者,对抗者或随机(自然者),自然者对像素的高斯混合模型 G ( Λ ( α ) ) G(\Lambda(\alpha)) G(Λ(α))进行采样,并随机选择操作指令。
可以注意到,最大化奖励需要最小化严重程度 s e v α ( α p ′ ) sev_{\alpha}(\alpha'_p) sevα(αp′),这正是定义2中问题的目标。如果 σ ( p ) \sigma(p) σ(p)是狄拉克分布,策略 σ \sigma σ是确定性的,如果对于所有有限路径 p p p, σ ( p ) = σ ( l a s t ( p ) ) \sigma(p)=\sigma(last(p)) σ(p)=σ(last(p)),策略σ是无记忆的。
定理1:当 o p t σ I I ∈ { m a x σ I I , m i n σ I I , n a t σ I I } opt_{\sigma_{II}}\in\{max_{\sigma_{II}},min_{\sigma_{II}},nat_{\sigma_{II}}\} optσII∈{ maxσII,minσII,natσII}时,确定性和无记忆策略足以满足玩家 I I I的需要。
蒙特卡罗树搜索渐近最优策略
本节中提出了一种基于蒙特卡罗树搜索(Monte Carlo Tree Search,MCTS)的方法来渐近地寻找最优策略。
首先考虑 o p t σ I I = m a x σ I I opt_{\sigma_{II}}=max_{\sigma_{II}} optσII=maxσII的情况,MCTS算法通过对模型 M ( α , p , d ) M(\alpha,p,d) M(α,p,d)的策略空间进行采样来逐步扩展部分博弈树。MCTS以置信区间上界算法(Upper Confidence Bound,UCB)作为探索方案,将其作为理论保证,当博弈树时被充分探索时,它会收敛至最优解。
使用两个终止条件 t c 1 tc_1 tc1和 t c 2 tc_2 tc2来控制算法的速度, t c 1 tc_1 tc1控制整个过程是否应终止, t c 2 tc_2 tc2控制何时进行移动,终止条件可以是例如迭代次数的界限等。
在部分树上,每个节点都维护有一对 ( r , n ) (r,n) (r,n),分别代表累积的奖励 r r r和访问次数 n n n。扩展叶节点以将其子级添加到部分树后,我们调用 S i m u l a t i o n Simulation Simulation在每个子节点上运行模拟。玩家在模拟过程中随机行动,每个模拟在到达终止节点 α 0 \alpha_0 α0时终止,在该节点上可以计算奖励 1 / s e v α ( α ′ ) 1/sev_{\alpha}(\alpha') 1/sevα(α′)。
然后,该奖励将从新子节点通过其祖先反向传播,直到到达根节点为止。每次通过节点反向传播新的奖励 v v v 时,我们都会将其关联对更新为 ( r + v , n + 1 ) (r+v,n+1) (r+v,n+1)。
b e s t C h i l d ( r o o t ) bestChild(root) bestChild(root)返回具有最高 r / n r/n r/n值的 r o o t root root的子代。
其他情况: o p t σ I I = n a t σ I I opt_{\sigma_{II}}=nat_{\sigma_{II}} optσII=natσII的情况,通过选择 G ( Λ ( α ) G(\Lambda(\alpha) G(Λ(α)来选择一个孩子,而不是选择最好的孩子;对于 o p t σ I I = m i n σ I I opt_{\sigma_{II}}=min_{\sigma_{II}} optσII=minσII的情况,选择最差的孩子。

游戏中的严重度区间:根据上面的MCTS算法,设 s e v ( M ( α , p , d ) , o p t σ I I ) sev(M(\alpha,p,d),opt_{\sigma_{II}}) sev(M(α,p,d),optσII)为 s e v α ( α ′ ) sev_{\alpha}(\alpha') sevα(α′), α ′ \alpha' α′即通过该算法得到的对抗样本,存在一个严重度区间 S I ( α , p , d ) SI(\alpha,p,d) SI(α,p,d):
[ s e v ( M ( α , p , d ) , m a x σ I I ) , s e v ( M ( α , p , d ) , m i n σ I I ) ] [sev(M(\alpha,p,d),max_{\sigma_{II}}),sev(M(\alpha,p,d),min_{\sigma_{II}})] [sev(M(α,p,d),maxσII),sev(M(α,p,d),minσII)]
此外, s e v ( M ( α , p , d ) , n a t σ I I ) ∈ S I ( α , p , d ) sev(M(\alpha,p,d),nat_{\sigma_{II}})\in SI(\alpha,p,d) sev(M(α,p,d),natσII)∈SI(α,p,d)。
通过最佳策略保障安全: τ \tau τ是像素操作中使用的操作幅度,如果对于所有维度 p ∈ P 0 p\in P_0 p∈P0,我们都有 ∣ α ′ ( p ) − α ( p ) ∣ = n ∗ τ ( n ≥ 0 ) |\alpha'(p)-\alpha(p)|=n*\tau(n\ge0) ∣α′(p)−α(p)∣=n∗τ(n≥0),则图像 α ′ ∈ η ( α , k , d ) \alpha'\in \eta(\alpha,k,d) α′∈η(α,k,d)是一个 τ \tau τ-网格图像。令 G ( α , k , d ) G(\alpha,k,d) G(α,k,d)是 η ( α , k , d ) \eta(\alpha,k,d) η(α,k,d)中的 τ \tau τ-网格图像的集合。对于玩家 I I II II是合作者的情况,我们有以下结论:
定理2:令 α ′ ∈ η ( α , k , d ) \alpha'\in \eta(\alpha,k,d) α′∈η(α,k,d)是任意一个 τ \tau τ-网格图像,使得 α ′ ∈ a d v N , k , d ( α , c ) \alpha'\in adv_{N,k,d}(\alpha,c) α′∈advN,k,d(α,c),那么我们有 s e v α ( α ′ ) ≥ s e v ( M ( α , p , d ) , m a x σ I I ) sev_{\alpha}(\alpha')\ge sev(M(\alpha,p,d),max_{\sigma_{II}}) sevα(α′)≥sev(M(α,p,d),maxσII)。
直观地讲,定理2是说该算法可以从 τ \tau τ-网格图像集中找到最佳对抗样本。
一个图像 α 1 ∈ η ( α , k , d ) \alpha_1\in \eta(\alpha,k,d) α1∈η(α,k,d)是一个关于 β > 0 \beta>0 β>0的错误分类集合,如果对于任何 α 2 ∈ η ( α 1 , 1 , β ) \alpha_2\in \eta(\alpha_1,1,\beta) α2∈η(α1,1,β),我们有 N ( α 2 ) ≠ N ( α ) N(\alpha_2)\ne N(\alpha) N(α2)=N(α)意味着 N ( α 1 ) ≠ N ( α ) N(\alpha_1)\ne N(\alpha) N(α1)=N(α)。我们有以下结论:
定理3:如果所有 τ \tau τ-网格图像都是关于 τ / 2 \tau/2 τ/2的错误分类聚合器,并且 s e v ( M ( α , p , d ) , m a x σ I I ) > d sev(M(\alpha,p,d),max_{\sigma_{II}})>d sev(M(α,p,d),maxσII)>d,那么 a d v N , k , d ( α , c ) = ∅ adv_{N,k,d}(\alpha,c)=\empty advN,k,d(α,c)=∅。
该定理表明,要实现完整的安全性验证,可以逐渐减小 τ \tau τ直到 s e v ( M ( α , p , d ) , m a x σ I I ) ≤ d sev(M(\alpha,p,d),max_{\sigma_{II}})\le d sev(M(α,p,d),maxσII)≤d,在这种情况下,网络是不安全的。
实验结果
对于本文的实验,我们让玩家 I I II II是合作者,它选择的对 ( X , i ) (X,i) (X,i)是这样的,对于所有的 ( x 1 , y 1 , z 1 ) , ( x 2 , y 2 , z 2 ) ∈ X (x_1,y_1,z_1),(x_2,y_2,z_2)\in X (x1,y1,z1),(x2,y2,z2)∈X,我们有 x 1 = x 2 , y 1 = y 2 x_1=x_2,y_1=y_2 x1=x2,y1=y2,即一个像素对于每个移动是变化的。当执行MCTS算法的 S i m u l a t i o n Simulation Simulation步骤时,对于所有关键点 λ ∈ Λ ( α ) \lambda\in \Lambda(\alpha) λ∈Λ(α),我们让 σ I ( λ ) = λ r / ∑ λ ∈ Λ ( α ) λ r \sigma_I(\lambda)=\lambda_r/ \sum_{\lambda\in \Lambda(\alpha)}\lambda_r σI(λ)=λr/∑λ∈Λ(α)λr,且 o p t σ I I = n a t σ I I opt_{\sigma_{II}}=nat_{\sigma_{II}} optσII=natσII,即玩家 I I I遵循随机策略,根据其响应强度选择一个关键点,玩家 I I II II是随机者。
我们将我们的方法与在两个图像分类网络上的两种最新方法进行比较,这两个网络是在基准数据集MNIST和CIFAR10上训练的。表1给出了与其他两种方法( C W CW CW和 J S M A JSMA JSMA)的比较。表中的数字是平均距离,定义为 1 1000 ⋅ ∑ i = 1 1000 ∣ ∣ α i − α i ′ ∣ ∣ 0 \dfrac{1}{1000}·\sum^{1000}_{i=1}||\alpha_{i}-\alpha'_{i}||_0 10001⋅∑i=11000∣∣αi−αi′∣∣0, α i ′ \alpha'_i αi′是根据MCTS算法计算出的 α i \alpha_i αi的对抗样本。

J S M A JSMA JSMA处理一个图像需要几分钟, C W CW CW比 J S M A JSMA JSMA慢10倍。
我们把本文提出的基于游戏的方法来支持实时决策和测试的可能性,对于这种情况,算法需要非常高效,只需要几秒钟就可以执行一项任务。我们将我们的方法应用到一个用于对从摄像头收集的交通灯图像进行分类的网络中。Nexar交通灯挑战赛公开了超过一万八千个交通灯图像。如果图像中出现的交通灯是绿色的,则每个图像被标记为绿色;如果图像中出现的交通灯是红色的,则标记为红色;如果图像中没有出现交通灯,则标记为空。我们测试了挑战的获胜者,其准确率超过90%。
尽管每个输入有37632维(112 x 112 x 3),我们的算法显示平均4.85维的操作就会改变网络分类。算法在0.303秒内处理了每幅图像(包括读取和写入图像的时间),即测试所有1000幅图像需要304秒。


总结
在本文中,我们提出了一种新的特征引导的黑盒算法,用于评估深度神经网络对对抗样本的抵抗能力。我们的算法采用SIFT方法进行特征提取,非常高效,在实时决策支持中具有广泛的应用前景。我们开发了一个软件包,并展示了它在各种最先进的分类网络上的适用性。未来有许多可能的方向,比如与贝叶斯推理方法进行比较,以识别对抗样本的例子。