【数据结构】 堆的简单理解和代码实现

前言：本章将详细介绍堆，并通过代码创建堆、实现一些堆的基本操作，最后以TopK问题为文章结尾。 By the way,咱们数据结构中的堆是一种数据结构，堆必然是完全二叉树，而系统层的堆是操作系统中管理内存的一块区域分段，注意区分开。

---

---

1.堆的概念、性质

什么是堆：

堆(Heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵完全二叉树的数组对象。

堆的性质：

1.堆中某个节点的值总是不大于或不小于其父节点的值；

2.堆总是一棵完全二叉树。

将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。常见的堆有二叉堆、斐波那契堆等。堆是非线性数据结构，相当于一维数组，有两个直接后继。

2.堆的代码实现和基本操作

定义堆

typedef int HPDataType;

//定义大堆
typedef struct Heap
{
     
	HPDataType* a;
	int size;
	int capacity;
}HP;

---

堆的向上调整

从叶子节点插入一个元素后，想要继续保持堆的结构不变。从下往上，对二叉树进行调整，确保最后是小堆。

图示过程如下：

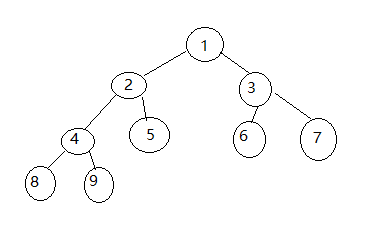
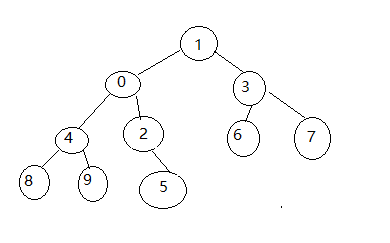
1.未进行插入新元素的堆：

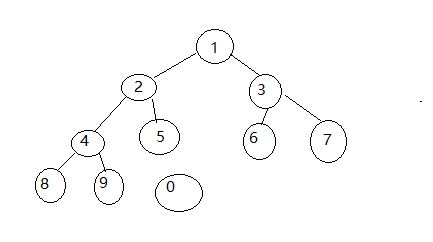
2.新元素0

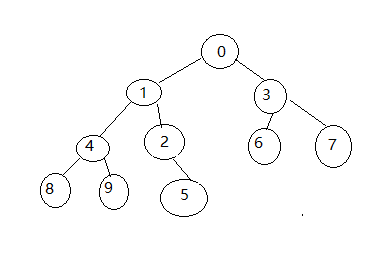
3.新元素0跟此时的父亲节点5比较，比5小，交换

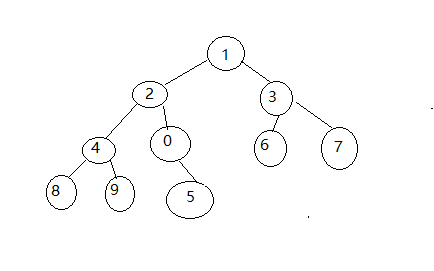
4.然后0继续和新的父亲节点2比较，比2小，交换

5.然后0继续和新的父亲节点0进行比较，比1小，交换

6.此时的child已经达到while (child > 0)的结束条件了，退出循环，新的小堆调整完毕。

void swap(int* px, int* py)
{
     
	int tmp = *px;
	*px = *py;
	*py = tmp;
}

//前提：原本的堆就是小堆
void AdjustUp(int* a, int child)
{
     
	int parent = (child - 1) / 2;
	//这里可以思考下为什么while的条件不适用parent>=0，因为parent不可能小于0
	while (child > 0)
	{
     
		//只要插入的叶子节点比父亲节点小就进行交换，并不断进行循环，直至达到结束条件
		if (a[child] < a[parent])
		{
     
			swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
     
			break;
		}
	}
}

---

堆的向下调整

比如当我们删除了堆顶第一个元素后，想要保持剩下的元素还是堆的结构时，可以考虑把最后一个叶子节点移动到堆顶，然后使用一次AdjustDown。

图示过程如下：

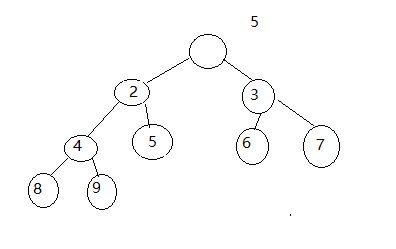
1.往堆顶插入新元素5

2.元素5跟左右孩子中小的那个进行比较，若比他大，就交换

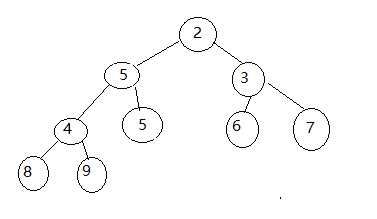
3.继续与左右孩子中小的进行比较，若更大，就交换

4.继续比较，发现并不会比孩子节点小，跳出循环，新的小堆调整结束。

//堆从上到下进行调整(前提条件是：左右子树都是小堆)
void AdjustDown(int* a, int n, int parent)
{
     
	int child = 2 * parent + 1;
	while (child < n)
	{
     
		//选出左右孩子当中小的那个孩子
		if (a[child + 1] < a[child])
		{
     
			child++;
		}

		//从上到下，如果小的那个孩子比父亲节点还小，那就交换
		if (a[child] < a[parent])
		{
     
			swap(&a[child], &a[parent]);
			//child = parent;
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
     
			break;
		}
	}
}

---

堆的初始化

这里以建立小堆为例，我们需要保证小堆的结构，这里通过自下而上进行调整。

这里提一嘴为什么建堆过程中的for循环内i初始值设置为（n-1-1）/2，首先数组最后一个元素下标是n-1,又有child=2*parent+1,带入后就是这个初始值。

void HeapInit(HP* php, int* a, int n)
{
     
	assert(php);

	php->a = (HPDataType*)malloc(sizeof(HPDataType) * n);
	if (php->a == NULL)
	{
     
		printf("malloc fail");
		exit(-1);
	}

	memcpy(php->a, a, sizeof(HPDataType) * n);

	//建堆，从下往上反复调用函数AdjustDown，建立小堆
	for (int i = (n - 1 - 1) / 2; i >= 0;--i)
	{
     
		AdjustDown(php->a, n, i);
	}

	php->size = n;
	php->capacity = n;
}

---

堆的销毁

直接free掉a，然后把php->a置空，并把size和capacity置0

void HeadDestroy(HP* php)
{
     
	assert(php);

	free(php->a);
	php->a = NULL;
	php->size = php->capacity = 0;
}

---

堆的插入操作

1.先判断下空间是否满了，若满了，realloc开辟一块新的空间，没满就不需要开辟。

2.然后把新插入的元素放在最后一个叶子节点处

3.接下来与其双亲结点进行比较,如果比双亲结点小,就交换其值,一直不断重叠

4.最后如果该数据比双亲结点值大,就结束调整;如果当child等于0,就结束调整

void HeadPush(HP* php, HPDatatype x)
{
     
	assert(php);

	if (php->size == php->capacity)
	{
     
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * 2 * php->capacity);
		if (php->a == NULL)
		{
     
			printf("realloc fail");
			exit(-1);
		}
		php->capacity *= 2;
	}

	php->a[php->size] = x;
	php->size++;

	//从下往上进行调整，保持堆的结构不变
	AdjustUp(php->a, php->size - 1);
}

---

堆的删除操作

该函数的作用是删除堆顶元素,并且不能毁坏堆结构，如果是你，你会写出怎样的代码来实现？

这里借助堆排序的思想,直接把堆顶第一个元素和堆底第一个元素交换，然后php->size减1，再调用一次自上而下的排序，因为size减1了，相当于除了原本堆顶第一个元素以外的元素进行调整。

void HeadPop(HP* php)
{
     
	assert(php);
	assert(!HeapEmpty(php));

	//这个地方太妙了 兄弟们！！！ 
	swap(&a[0], a[php->size - 1]);
	php->size--;

	AdjustDown(php->a, php->size, 0);
}

---

获取堆顶的元素

HPDataType HeapTop(HP* php)
{
     
	assert(php);
	assert(!HeapEmpty(php));

	return php->a[0];
}

---

堆的判空

bool HeadEmpty(HP* php)
{
     
	assert(php);

	return php->size == 0;
}

---

堆内元素数量

int HeapSize(HP* php)
{
     
	assert(php);

	return php->size;
}

---

打印堆内元素

void HeapPrint(HP* php)
{
     
	assert(php);

	for (int i = 0; i < php->size; i++)
	{
     
		printf("%d",php->a[i]);
	}
}

---

3.TopK问题(即在N个数当中，选出最大/小的K个元素)

例：从（N）10亿个整数当中挑选最大的（K）10个，怎么做？

首先思考下建立大堆还是小堆？

答：建小堆，因为如果建大堆，最大的数可能挡在头的位置，其他9个次大的数就进不来。

接下来怎么建这个拥有10亿个整数的堆呢？

思路一：建一个拥有10亿个数的小堆，建堆的时间复杂度是O(N)，K个数选出来是O（KlogN），时间复杂度为O(N+KlogN)，这个复杂度太高了，能不能优化下？

思路二：建一个10个数的小堆，将10个数以外的数依次放入堆中，建堆的时间复杂度O(K)，找到K个数的时间复杂度为（NlogK），总时间复杂度就是O(K+N*logK)。

复现思路二的代码：

void PrintTopK(int* a, int n, int k)
{
     
	HP hp;
	HeapInit(&hp, a, k);

	for (int i = k; i < n; ++i)
	{
     
		if (a[i] > HeapTop(&hp))
		{
     
			HeapPop(&hp);
			HeapPush(&hp, a[i]);
		}
	}

	HeapPrint(&hp);

	HeapDestroy(&hp);
}

void TestTopk()
{
     
	int n = 100000;
	int* a = (int*)malloc(sizeof(int) * n);
	srand(time(0));
	for (size_t i = 0; i < n; ++i)
	{
     
		a[i] = rand() % 1000000;
	}
	//随机赋值十个最大的数
	a[5] = 1000000 + 1;
	a[1231] = 1000000 + 2;
	a[531] = 1000000 + 3;
	a[5121] = 1000000 + 4;
	a[115] = 1000000 + 5;
	a[2335] = 1000000 + 6;
	a[9999] = 1000000 + 7;
	a[76] = 1000000 + 8;
	a[423] = 1000000 + 9;
	a[3144] = 1000000 + 10;

	PrintTopK(a, n, 10);
}

---

补充下将一个顺序表整理成堆的时间复杂度推导：

---

4.源码链接

https://gitee.com/linkylo/c_code_2021/tree/master/c_code_2021_9_3(Lab%EF%BC%89

---

数据结构堆的代码实现和相关的TopK问题的内容到此介绍结束了，感谢您的阅读！！！如果内容对你有帮助的话，记得给我点个赞——做个手有余香的人。