8.7 Meta learning元学习全面理解、MAML、Reptile

8.7 Meta learning元学习全面理解、MAML、Reptile

8.8LSTM作为元学习器学习梯度下降

1、介绍

元学习Meta learning = 学习如何去学习Learn to learn

为什么需要元学习？

传统深度学习需要大数据，因为使用随机梯度下降更新参数，需要数据进行缓慢地学习。当遇到新数据时，模型必须低效地重新学习它们的参数，以便在不产生灾难性干扰的情况下充分整合新信息。

但是人类在很少的样本学习——例如，一个孩子可以从一本书中的一张图片概括出“长颈鹿”的概念。这激发了我们的兴趣:“one-shot”学习，即从一个单一的例子中学习，和few-shot 学习 即从小样本中学习，和zero-shot 学习 即零样本中学习。这些都和元学习有关，元学习是快速学习的算法。

元学习是对模型的一种研究与学习。相对于deep learning在一个task（任务）中通过对样本的学习以对新样本做出判断，元学习的目标可以看做是将task视作样本，通过对多个task学习元知识和快速学习的能力，以使元模型（meta-learner）能够对新的task做出快速而准确的预测。它研究的不是如何提升模型解决某项具体的任务（分类，回归，检测）的能力，而是研究如何提升模型解决一系列任务的能力。

举个例子就是，机器之前学习了100个task，之后机器学习第101个task的时候，会因为之前学习的100个task所具有的知识，而让第101个task表现得更好。比如说第一个任务是语音识别，第二个任务是图像识别，第一百个任务是文本分类，机器因为之前所学到的任务，所以在后面的任务学习的更好。

这个和life long learning有什么区别吗！好像很像诶。确实，life long learning和meta learning都是要根据以往的task，希望对现在的task有所帮助，但是meta learn所要求的是学习新的task时候有新的model（训练后的），但是life long learning始终是一个模型。

和Life-long方法有所不一样：

方法	区别
Life-long	一个模型适用于所有任务
Meta	如何学习一种新的模型

few-shot learning

few-shot learning——小样本学习，是指通过极少的样本学习获得（监督/非监督）回归、分类模型。在现有的研究成果中，小样本学习可以基于fine-tune、metric(如孪生网络)、基于meta-learning等。在基于meta-learning的少样本学习中，已有memory-augmented neural networks (Santoro et al., 2016)、meta-learner LSTM (Ravi & Larochelle, 2017)等经典学习方法。

小样本学习一直和元学习系紧密。元学习的目标就是通过学习大量的task ，从而学习到内在的元知识，从而能够快速的处理新的同类任务，这和少样本学习的目标设定是一样的。我们也希望通过很多task来学习识别物体这种能力，从而面向新的少样本学习任务，能够充分利用已经学习到的识别能力（也就是元知识），来快速实现对新物体的识别。而在这里，通过前面的分析，我们明白了，我们要研究如何通过元学习的方式来让神经网络学会比较这个元知识能力。

reinforcement learning

相比于深度学习，强化学习的训练样本没有标签，是通过环境与决策的奖惩政策来进行学习。强化学习的过程是动态的，强调与环境进行交互，其优势在于解决决策问题，如推荐系统等。在本文中，MAML不仅可适用于few-shot learning，也同样适用于强化学习。

2、概念

机器学习：用Training Data训练由我们设计的Learning Algorithm，得到一个最优算法$f^{\ast }$ ，可以用来完成相应的任务（猫狗识别）

meta learning方法是：依旧给模型很多训练数据，我们将Learning Algorithm当作是一个$F$（function），我们需要$F$做的事生成另一个$f^{\ast }$（function），而这个f可以用来做影像识别。我们meta learning的方法就是找到$F$。

Machine Learning ≈ 根据数据找一个函数 f 的能力

meta learning：用$D_{train}$ 训练由我们设计的F，得到一个完成相应任务的$f^{\ast }$函数 ，怎么感觉和上面没什么区别？

其实不一样，Meta Learning≈ 根据数据找一个找一个函数 f 的函数 F 的能力。$F$的输入是训练数据，输出是解决一个小问题的$f$,即
$$f^{\ast }=F\left(D_{\text{train }}\right)$$

机器学习中是知道函数$f$，而是训练函数f的参数；机器学习的方法可以简单理解为三步：

1. 定义一个function 集合

2. 找到一个$f$好坏的度量指标（loss function）

3. 在这个集合中寻找最好的$f$

元学习是不知道函数$f$，而是训练函数F找到$f$（含参数）。

我们meta learning的方法和machine learning的方法是十分相似的，也是三步：

1. 定义一组learning algorithm $F$的集合，

2. 定义一个判别learning algorithm 好坏的方法

3. 找一个最好的learning algorithm做为$F$。

3、 Meta learning 三个步骤

定义一组learning algorithm

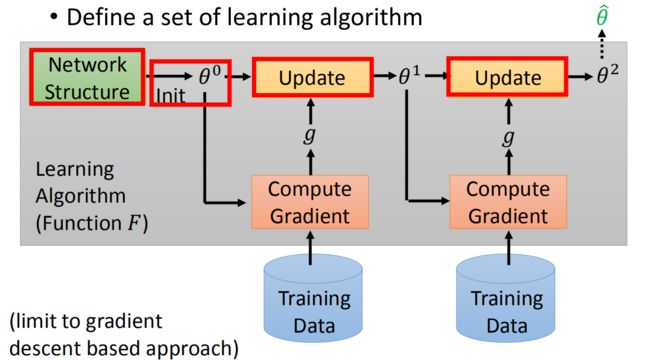
首先，看看如何设置一个learning algorithm set。先来看机器学习中是如何进行learning algorithm的。以基于GD优化的算法为例，先是定义了一个神经网络结构，之后初始化参数值，之后根据训练数据计算梯度，更新参数，图中的每一步的gradient $g$其实不一样，最后得到最优的参数。

红色的格子都是人为设定的，网络结构的选择，参数的初始化，参数更新的方法，都是人为设计的，红框中如果我们定义不同的东西，实际上就是不同的算法。

那么这些部分能否是机器自己设计呢！我们参数的初始值能不能让机器自己初始化呢！假设机器自己初始化参数，机器自己选择参数更新方法，机器自己选择神经网络结构，这就是我们meta learning的learning algorithm set。

Meta Learning 就是把这些 人为设定的模块由机器自行设计，使网络有更强的学习能力和表现。

损失函数

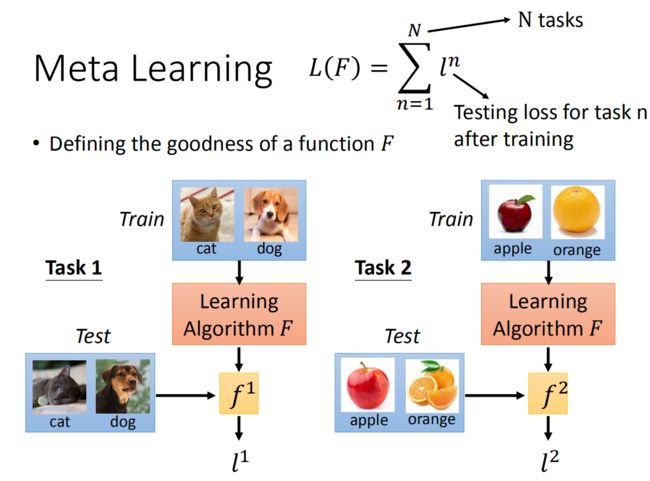
这个过程的损失函数：比如我们用一个learning algorithm $F$。首先用$F$进行猫狗分类器的学习，之后得到了一个$f^1$，$f^1$的训练数据进行测评，得到$f^1$的loss function $l^1$。之后再用$F$进行苹果橘子分类器的学习，得到一个$f^2$，$f^2$的训练数据进行测评，得到$f^2$的loss function $l^2$。

这里用$F$完成n个分类task，之后对每一个task求一个$l$。之后我们把所有的$l$都加在一起，就变成了我们最后的损失函数$L(F)$。我们就是使用$L(F)$来评估F的。

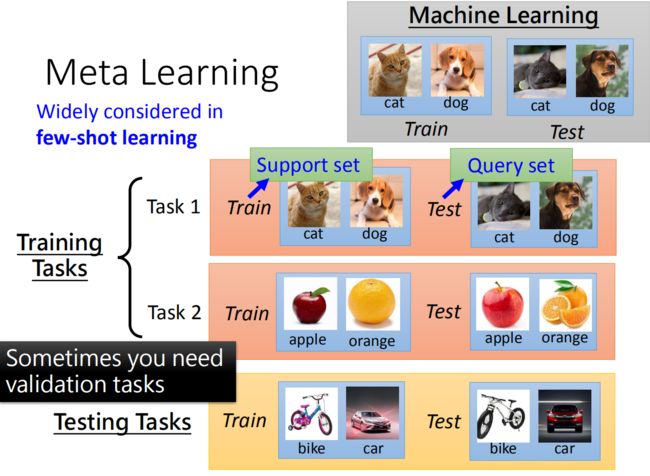
从这里可以看到机器学习和元学习在数据上不一样。一般的机器学习任务是单任务的，所以数据集是一堆训练数据，和测试数据。但是在meta learning的任务是多任务的，所以在这种情况下，我们需要做的是将很多的任务分为训练任务和测试任务，之后每一个小的任务都有训练数据和测试数据。比如说一共有十个任务，我们将其中的八个作为是训练任务，剩余的两个作为测试任务，其中每一个任务都有自己的测试数据和训练数据。以此来检测meta learning的学习能力。

这里要说明：

1. 由于元学习有多个任务，每个任务如果有很多数据，那么训练时间会很长很长，因此，元学习中每个任务的数据不会很多，所以元学习也叫few-shot learning，为了和机器学习区分开，训练和测试数据分别叫Support set和Query set。
2. 和机器学习一样，当我们的元学习中的训练任务很多的时候，我们可以将其中一部分切出来作为验证任务：validation tasks。
3. 元学习中的testing task可以和training task一样，也可以不一样。

寻找最好的F

meta learning损失函数，就是$L（F）$，其实就是每一个训练子任务loss function总和。之后我们用梯度下降的方法不断的更新$F$的参数，得到一个最好的$F^{\ast }$，之后我们将训练好的$F^{\ast }$放入到测试任务集中进行测试，如图，比如第一个测试任务是一个自行车汽车识别器，我们先将少量训练数据放入到$F^{\ast }$中，之后得到一个分类器$f^{\ast }$，之后我们将测试数据放入到$f^{\ast }$中，得到最终的loss，作为这次测试的结果。

4、元学习过程总结

设$\mathcal{X}$为输入的空间， 和$\mathcal{Y}$是一个离散的标签空间。设$\mathcal{D}$为$\mathcal{X}\times \mathcal{Y}$的分布。监督机器学习通常旨在通过对参数化模型和训练集应用学习算法捕获条件分布$p(y\mid x)$， $S_{\text{train}}=$ ${\left\{\left(x_i,y_i\right)\sim \mathcal{D}\right\}}_{i=1}^N.$在推理时，模型在测试输入$x$上进行评估，以估计$p(y\mid x)$。推理和学习算法的组合可以写成函数$h$(一种分类算法)以训练集作为输入，还有测试时输入$x$，并在标签上输出估计概率分布$\hat{\mathbf{p}}$:
$$\hat{\mathbf{p}}(x)=h\left(x,S_{\text{train }}\right)$$
在few-shot学习中，我们希望函数$h$即使在$S_{\text{train}}$很小的情况下也具有较高的分类精度。Meta learning是一个涵盖了许多提出的经验风险最小化方法的术语。具体来说，他们考虑了参数化分类算法$h(\cdot ，\cdot ;\mathbf{w})$，并尝试估计一个“好的”参数向量$\mathbf{w}$，即对应于一个可以很好地从小数据集学习的分类算法。因此，学习这个参数向量可以理解为元学习。

因此学会获取元知识能力的方法有三种：

• 特定的网络结构
• 改变网络的初始化参数
• 参数更新的方法

元学习的目标是针对任务训练而不是数据点。每个任务${\mathcal{T}}_i$ 都是独立的，其输入为$x_t$，输出为$y_t$，损失函数是${\mathcal{L}}_i\left(x_t,y_t\right)$，一个转移分布$P_i\left(x_t\mid x_{t-1},y_{t-1}\right)$，任务大小$H_i$ .一个元学习器建模分布：$\pi \left(y_t\mid x_1,\dots ,x_t;\mathbf{w}\right)$. 给定任务的分布 $\mathcal{T}=P\left({\mathcal{T}}_i\right)$, 元学习者的目标是使$\mathbf{w}$的预期损失最小化。
$$\begin{array}{rl}\underset{\mathbf{w}}{\min }& {\mathbb{E}}_{{\mathcal{T}}_i\sim \mathcal{T}}\left[\sum _{t=0}^{H_i}{\mathcal{L}}_i\left(x_t,y_t\right)\right]\\ \text{ where }{x}_t& \sim P_i\left(x_t\mid x_{t-1},y_{t-1}\right),y_t\sim \pi \left(y_t\mid x_1,\dots ,x_t;\mathbf{w}\right)\end{array}$$
元学习器通过优化从$\mathcal{T}$中采样的任务(或小批任务)的预期损失来进行训练。在测试过程中，对元学习者进行没遇见过的任务评估，这些任务来自不同的任务分布$\mathcal{T}=P\left({\mathcal{T}}_i\right)$，与训练任务分布$\mathcal{T}$类似。

元学习算法有两个阶段。第一阶段是元训练，估计分类算法的参数向量$\mathrm{w}$。

• 在元训练过程中，元学习器可以访问一个大型标记数据集$S_{\text{meta}}$，该数据集通常包含大量类的数千张图像$C$ . 在元训练的每次迭代中，元学习器从 $S_{\text{meta}}$中抽取一个分类问题样本。也就是说，元学习器首先从$C$中抽取$m$类的子集，然后抽取小的"training" 集合 $S_{\text{train }}$ 和小的"test" 集合 $S_{\text{test }}.$
• 然后，它使用当前的权重向量$\mathbf{w}$来计算条件概率$h\left(x,S_{\text{train}};\mathbf{w}\right)$用于测试集$S_{\text{test}}$中的每一个点$(x,y)$。注意，在这个过程中，$h$可能执行相当于对$S_{\text{train}}$进行“training”的内部计算。根据得到的预测，$h$会对于当前$S_{\text{test}}$ 中的每个点造成损失$L\left(h\left(x,S_{\text{train }};\mathbf{w}\right),y\right)$ 。
• 然后元学习器反向传播总损失的梯度 ${\sum }_{(x,y)\in S_{\text{test }}}L\left(h\left(x,S_{\text{train }};\mathbf{w}\right),y\right)$。每次迭代的类数$m$和每个类的最大训练样本数$n$是超参数。

第二阶段是元测试阶段，将生成的分类算法用于解决新的分类任务:对每个新任务，分别给出有标记的训练集和未标记的测试示例，分类算法输出类概率。

元学习task定义

元学习的论文中多次出现名词task，模型的训练过程都是围绕task展开的，要正确地理解task，我们需要了解的相关概念包括${\mathcal{D}}_{meta-train}$ ,${\mathcal{D}}_{meta-test}$, support set, query set, meta-train classes, meta-test classes等等。

我们假设这样一个场景：我们需要利用元学习算法训练一个数学模型模型 $M_{fine-tune}$ ，目的是对未知标签的图片做分类。

${\mathcal{D}}_{meta-train}$ 含有10个类别的图片 $C_1～C_{10}$ 即meta-train classes（每类30个已标注样本），用于帮助训练元学习模型 $M_{meta}$ 。

${\mathcal{D}}_{meta-test}$含有 5个类别数据 $P_1～P_5$ 即meta-test classes（每类5个已标注样本用于训练。另外每类有15个已标注样本用于测试），注意这里的数据和${\mathcal{D}}_{meta-train}$不一样，即未知标签的图片，是用于训练和测试 $M_{fine-tune}$ 的数据集。

训练过程，元学习者首先利用 $C_1～C_{10}$ 的数据集训练元模型$M_{meta}$，再在$P_1～P_5$的数据集上精调（fine-tune）得到最终的模型 $M_{fine-tune}$ 。我们的实验设置为5-way 5-shot。

根据5-way 5-shot的实验设置，我们在训练$M_{meta}$ 阶段，从 $C_1～C_{10}$ 中随机取5个类别，每个类别再随机取20个已标注样本，组成一个task $\mathcal{T}$ 。其中的5个已标注样本称为 $\mathcal{T}$ 的support set，另外15个样本称为 的**$\mathcal{T}$query set**。这个task $\mathcal{T}$ ， 就相当于普通深度学习模型训练过程中的一条训练数据。那我们肯定要组成一个batch，才能做随机梯度下降SGD对不对？所以我们反复在训练数据分布中抽取若干个这样的task $\mathcal{T}$ ，组成一个batch。在训练 $M_{fine-tune}$ 阶段，task、support set、query set的含义与训练 $M_{meta}$ 阶段均相同。

5、Meta Learning实例：Omniglot

N-way K-shot

N-way K-shot是few-shot learning中常见的实验设置。few-shot learning指利用很少的被标记数据训练数学模型的过程，这也正是MAML擅长解决的问题之一。N-way指训练数据中有N个类别，K-shot指每个类别下有$K$个被标记数据。

既然 Meta Learning 是 learn to learn，那么如何证明 Meta Learning 算法的有效性呢？显而易见，只需要证明用这种算法得到的网络模型学习能力很强就行了。具体到我们的 MAML 和 Reptile，只需要证明，用它们这些算法初始化之后的神经网络，在新的任务上训练，其收敛速率与准确率比从随机初始化的神经网络要高。

这里所谓“新任务”，一般是指难度比较大的任务，毕竟难度大的任务才有区分度嘛，要是都像 MNIST 数据那么简单，随便一训练就 99% 的准确率，也看不出网络初始化参数所起的作用了。因此一般用 few-shot learning 的任务来评估 Meta Learning 算法的有效性。所谓 few-shot learning，就是指每类只有少量训练数据的学习任务（MNIST 每个数字都有上万张训练图片，因此不是 few-shot learning）。数据集 Omniglot：，是一个类似 MNIST 的手写数据集，如下图所示。该数据集包含 1623 类，每类只有 20 个训练数据，因此它属于 few-shot learning 的范畴，经常作为 benchmark 用来衡量 Meta Learning 算法的性能。

https://github.com/brendenlake/omniglot

• 1623 characters，部分字符：

每一个字符有20个例子，20个例子都是这个标签对应的不同的人写下的例子。

我们这个数据集究竟应该如何去使用呢！我们将整个数据集分为很多的N-ways K-shot classfication的任务。N-ways就是分为N类，K-shot就是每一类种有K个样本。就是一个总共类别有N类，每一类有K个样本的分类器。

举个例子20 ways 1 shot就是总共20类，每一类有1个样本的分类器。上图就是一个20 ways 1 shot的分类器，训练集就是20类，每一类就只有一张图片的图片集。测试集就是一张图片，我们可以看到测试集和训练集中最下面一行中间的那个是一类的。

在我们使用Omniglot数据集的时候，我们先将其中的1623类拆分为训练集和测试集，之后我们再在训练集中采样出$N$类，每一类采样$K$个样本作为我们的一个分类任务，当然我们的训练集可以被拆分组合为很多分类任务的。

我们测试集是在测试类中采样出$n$类，每一类采样$k$个样本作为我们的测试分类任务。当我们的$F$在训练集中被训练好以后，我们就开始将其放入到test中进行测试。

参数初始化

训练神经网络的第一步是初始化参数。当前大多数深度学习框架都收录了不同的参数初始化方法，例如均匀分布、正太分布，或者用 xavier_uniform，kaiming_uniform，xavier_normal，kaiming_normal等算法。除了用随机数，也可以用预训练的网络参数来初始化神经网络，也就是所谓 transfer learning，或者更准确地说是 fine-tuning 的技术。

fine-tuning 之所以能 work，是因为预训练的神经网络本身就有很强的特征提取能力，能够提取很多有含义的特征，例如毛皮，耳朵，鼻子，眼睛，分辨猫狗，只需要知道这些特征是如何组合的就好了，这比从头开始学习如何提取毛皮、耳朵、鼻子等特征要高效得多。

预训练的网络比随机初始化的网络有更强的学习能力，因此 fine-tuning 也算是一种 Meta Learning 的算法。它和我们今天要介绍的 MAML 和 Reptile 都是通过初始化网络参数，使神经网络获得更强的学习能力，从而在少量数据上训练后就能有很好的性能。

下面我们来介绍两种meta learning的方法，分别是maml和reptile。前者是2017年的paper，后者是2018年的paper。

6、MAML

目标函数

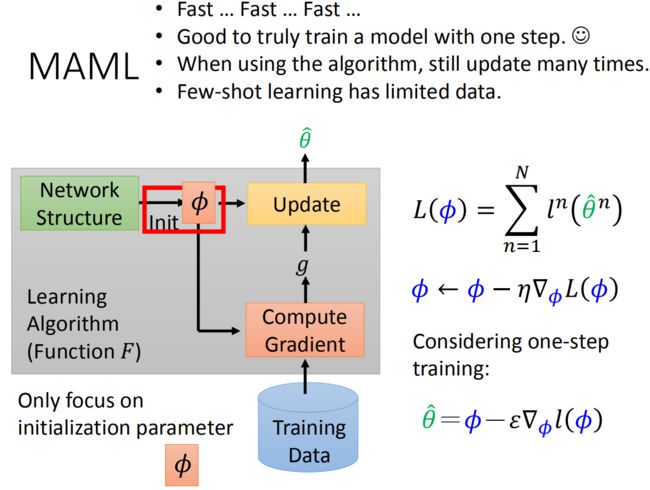
MAML主要是关注初始化参数 $\varphi$ 的选择（所有task的Network Structure都是一样的）。其损失函数为：
$$L(\varphi )=\sum _{n=1}^N{l}^n({\hat{\theta }}^n)$$
其中：

${\hat{\theta }}^n$ : 在第$n$个测试任务上训练之后的模型参数， ${\hat{\theta }}^n$ 依赖于 $\varphi$ , $l^n({\hat{\theta }}^n)$: 任务$n$的loss ，在任务 $n$ 的测试集上得出。

MAML的框架是两层的循环嵌套，外面这层是更新MAML模型的参数 $\varphi$，然后里面这层是更新任务的参数 ${\hat{\theta }}^n$ ，当然这个内部循环只更新一次（实际是两次）。

使用Gradient Descent来最小化 $L(\varphi )$
$$\varphi \leftarrow \varphi -\eta {\nabla }_{\varphi }L(\varphi )$$
可能很多人看到meta learning的更新参数方法以后就会想到迁移学习中的model pre-training（ pre-training： 假设task2的训练集太小不好训练，我们将和task2相似的task1作为先导数据集，进行训练，将训练的结果作为task2的初始化）。

这里要和transfer learning中的pre-train model的损失函数进行区分:
$$L(\varphi )=\sum _{n=1}^N{l}^n(\varphi )$$
那么这两种方法有什么区别呢，可以看到transfer learning是用现有的模型去计算Loss (看模型的当前表现) 而MAML是用 $\varphi$ 训练之后的模型来计算Loss (看模型潜力) 用图形来表示二者的区别吧

MAML vs transfer learning

对于MAML, 我们不在意 $\varphi$ 在 training task 上表现如何, 我们在意用 $\varphi$ 训练出来的 ${\theta }^n$ 表现如何，例如图中的 $\varphi$, 在task 1和task 2上目前表现并不是最好的, 但是在task 1上, 如果顺着左边的黑色箭头梯度下降，最终可以得到 ${\hat{\theta }}^1$; 在task 2上，如果顺着右边的黑色箭头梯度下降，最终可以得到 ${\hat{\theta }}^2$ 。

这两个都是最好的结果（全局最优）,所以这就是一个好的$\varphi$.

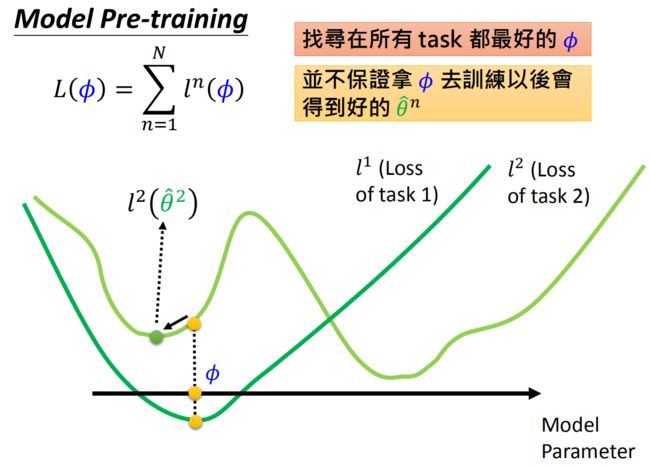
对于transfer learning，我们寻找在所有task都最好的 $\varphi$，但并不能保证把 $\varphi$拿去训练以后会得到最好的${\theta }^n$ ，例如图中 $\varphi$在task 1上得到最好的结果，但是拿到task 2上却只能得到一个局部最小值。

总结一下就是，Model Pre-training方法想要得到的参数 $\varphi$就是在任何task上都表现良好的参数。但是MEML想要得到的参数是在任务task中经过训练集训练所能得到的比较好的参数。

Model Pre-training看重 $\varphi$ 现在的表现，但是Meml看重 $\varphi$未来的潜力。

MAML的训练

总结起来, MAML算法的框架其实很简单, 值得注意的是两个学习率 $ϵ$ 和 $\eta$ 所用的地方不同:

1. 对于采样出来的所有任务 ${\theta }^i$, 在support set上计算梯度并更新参数 ${\theta }^i=\varphi -ϵ{\nabla }_{\varphi }l(\varphi )$
2. 计算所有任务在query set上的损失之和 $L(\varphi )={\sum }_{n=1}^N{l}^n\left({\theta }^n\right)$
3. 更新初始化参数 $\varphi \leftarrow \varphi -\eta {\nabla }_{\varphi }L(\varphi )$

MAML更新参数的过程中，一般只会更新一次：
$$\hat{\theta }=\varphi -ϵ{▽}_{\varphi }l(\varphi )$$
原因如下：

1，我们的meta learning有很多的任务，假设每一个任务都要更新很多次参数的话，会很慢，所以我们为了追求速度，就让模型只更新一次就好。

2，我们本来的想法就是希望模型非常棒,参数$\varphi$仅仅更新一次就得到这个子任务task的参数$\theta$

3，当我们训练的时候，我们仅仅是让其更新一次，但是当我们真实测试的时候，我们往往可以更新无数次

4，我们的few-shot learning本身就是没有多少训练集，防止over fitting所以我们往往希望可以一次更新就得到参数。

MAML Toy Example

Each task:

• 给定一个正弦函数 $y=a\text{sin}(x+b)$ 作为target function；

• 从正弦函数中采样K个点作为样本；

• 用这K个样本来估计target function。

每一个task就是通过sample出的点还原最开始的方程式。我们可以不断的改变a和b的值，实现多个不同的任务，从而跑我们的mate learning。

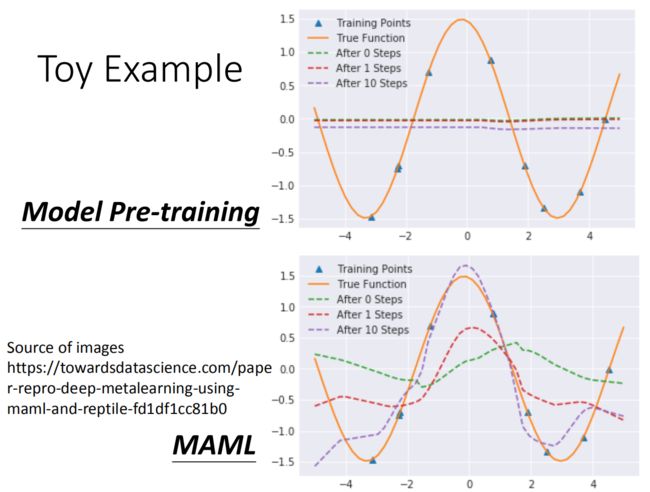
Model Pre-training做出的结果如下图所示：由于Model Pre-training是在所有task都最好的初始化 $\varphi$，这里所有的正弦函数叠起来就是一条直线，所以它初始就是直线。训练几次以后，仍然是水平线。

但是使用maml就大不相同，maml一开始的参数是一条波浪线，在训练一次以后大概可以知道哪里是波峰，训练十次以后，波峰和波谷几乎可以发现。

论文中是把maml和其他的meta learning方法做比较，发现maml的方法是比较好的。

算法

考虑一个由参数化函数$f_{\theta }$表示的模型，参数为$\theta$。当适应一个新任务${\mathcal{T}}_i$时，模型的参数$\theta$变成${\theta }_i^{\prime }$。更新的参数向量${\theta }_i^{\prime }$是通过在任务${\mathcal{T}}_i$上使用一个或多个梯度下降更新来计算的。例如，当使用一个梯度更新时，
$${\theta }_i^{\prime }=\theta -\alpha {\nabla }_{\theta }{\mathcal{L}}_{{\mathcal{T}}_i}\left(f_{\theta }\right)$$
步长$\alpha$可以固定为超参数或meta-learned。为了简单起见，将在其余部分考虑一个梯度更新，但是使用多个梯度更新是一个简单的扩展。

通过优化$f_{{\theta }_i^{\prime }}$相对于$\theta$的改进来训练模型参数，这些任务是从$p(\mathcal{T})$采样的。更具体地说，meta目标如下:
$$\underset{\theta }{\min }\sum _{{\mathcal{T}}_i\sim p(\mathcal{T})}{\mathcal{L}}_{{\mathcal{T}}_i}\left(f_{{\theta }_i^{\prime }}\right)=\sum _{{\mathcal{T}}_i\sim p(\mathcal{T})}{\mathcal{L}}_{{\mathcal{T}}_i}\left(f_{\theta -\alpha {\nabla }_{\theta }{\mathcal{L}}_{{\mathcal{T}}_i}\left(f_{\theta }\right)}\right)$$
注意meta-优化执行模型参数$\theta$, 而目标是使用更新的模型参数${\theta }^{\prime }$计算的,meta方法旨在优化模型参数，以便在新任务上使用一个或少量梯度步骤将在该任务上产生最大效率的行为。

通过随机梯度下降(SGD)进行跨任务元优化，将模型参数$\theta$更新如下:
$$\theta \leftarrow \theta -\beta {\nabla }_{\theta }\sum _{{\mathcal{T}}_i\sim p(\mathcal{T})}{\mathcal{L}}_{{\mathcal{T}}_i}\left(f_{{\theta }_i^{\prime }}\right)$$
其中$\beta$是元步长。在一般情况下，完整的算法在算法$1.$中概述

第一个Require指的是在 ${\mathcal{D}}_{meta-train}$中task的分布。结合我们在上一小节举的例子，这里即反复随机抽取task $\mathcal{T}$ ，形成一个由若干个（e.g., 1000个） $\mathcal{T}$ 组成的task池，作为MAML的训练集。有的小伙伴可能要纳闷了，训练样本就这么多，要组合形成那么多的task，岂不是不同task之间会存在样本的重复？或者某些task的query set会成为其他task的support set？没错！就是这样！我们要记住，MAML的目的，在于fast adaptation，即通过对大量task的学习，获得足够强的泛化能力，从而面对新的、从未见过的task时，通过fine-tune就可以快速拟合。task之间，只要存在一定的差异即可。再强调一下，MAML的训练是基于task的，而这里的每个task就相当于普通深度学习模型训练过程中的一条训练数据。

第二个Require就很好理解啦。step size其实就是学习率，读过MAML论文的小伙伴一定会对gradient by gradient这个词有印象。MAML是基于二重梯度的，每次迭代包括两次参数更新的过程，所以有两个学习率可以调整。

以上面的5-way 5-shot例子为例，这里我们简单叙述下MAML的算法流程。

• 1. 上面我们已经将数据区分成了 ${\mathcal{D}}_{meta-train}$和 ${\mathcal{D}}_{meta-test}$ ，在 ${\mathcal{D}}_{meta-train}$和 ${\mathcal{D}}_{meta-test}$中我们又将数据区分了support set,query set
• 2. 我们用于训练的模型是 $M_{meta}$ （初始化参数为 $\varphi$ ），这可能是一个输出节点为5的CNN，训练的目的是为了使得模型有较优秀的初始化参数。最终我们想要学出可以用于数据集 ${\mathcal{D}}_{meta-test}$分类的模型是 $M_{fine-tune}$ ， $M_{fine-tune}$ 和 $M_{meta}$ 的结构是一模一样的，不同的是模型参数。
• 3. 我们将1个任务task的support set去训练 $M_{meta}$ ，这里进行第一种梯度下降，假设每个任务只进行一次梯度下降，也就是 ${\hat{\theta }}^1\Leftarrow \varphi -ϵ.\partial l(\varphi )/\partial \varphi$ 。那么执行第2个task训练时，有 ${\hat{\theta }}^2\Leftarrow \varphi -ϵ.\partial l(\varphi )/\partial \varphi$ 。执行第batch size个task后，有 ${\hat{\theta }}^{bz}\Leftarrow \varphi -ϵ.\partial l(\varphi )/\partial \varphi$ ，如下图所示。

• 4. 上述步骤3用了batch size个task对 $M_{meta}$ 进行了训练，然后我们使用上述batch 个task中query set去测试参数为${\hat{\theta }}^i,i\in [1,batchsize]$ 的 $M_{meta}$ 模型效果，获得总损失函数 $L(\varphi )={\sum }_{i=1}^{bs}{l}^i({\hat{\theta }}^i)$ ，这个损失函数就是一个batch task中每个task的query set在各自参数为 ${\hat{\theta }}^i,i\in [1,batchsize]$ 的 $M_{meta}$ 中的损失 $l^i({\hat{\theta }}^i)$ 之和。
• 5. 获得总损失函数后，我们就要对其进行第二种的梯度下降。即更新初始化参数 $\varphi$ ，也就是 $\varphi \Leftarrow \varphi -\eta .\partial L(\varphi )/\partial \varphi$ 来更新初始化参数。这样不断地从步骤3开始训练，最终能够在数据集上获得该模型比较好的初始化参数。
• 6. 根据这个初始化的参数以及该模型，我们用数据集 ${\mathcal{D}}_{meta-test}$ 的support set对模型进行微调，这时候的梯度下降步数可以设置更多一点，不像训练时候（在第一次梯度下降过程中）只进行一步梯度下降。
• 7. 最后微调结束后，使用${\mathcal{D}}_{meta-test}$ 的query set进行模型的评估。

梯度数学推导

GD更新公式为:
$$\varphi \leftarrow \varphi -\eta {\nabla }_{\varphi }L(\varphi )\text{\hspace{1em}(1)}$$
其中损失函数为每个任务的 loss累加
$$L(\varphi )=\sum _{n=1}^N{l}^n\left({\hat{\theta }}^n\right)\text{\hspace{1em}(2)}$$
其中参数 ${\hat{\theta }}^n$ 的计算公式为一步更新：
$$\hat{\theta }=\varphi -ϵ{\nabla }_{\varphi }l(\varphi )\text{\hspace{1em}(3)}$$
公式1中的梯度优化首先要计算损失函数的梯度：
$${\nabla }_{\varphi }L(\varphi )={\nabla }_{\varphi }\sum _{n=1}^N{l}^n\left({\hat{\theta }}^n\right)=\sum _{n=1}^N{\nabla }_{\varphi }{l}^n\left({\hat{\theta }}^n\right)$$
下面来看梯度 ${\nabla }_{\varphi }l(\hat{\theta })$ 的求法, 实际上是对每一项求偏导:
$${\nabla }_{\varphi }l(\hat{\theta })=\left[\begin{array}{c}\partial l(\hat{\theta })/\partial {\varphi }_1\\ \partial l(\hat{\theta })/\partial {\varphi }_2\\ ⋮\\ \partial l(\hat{\theta })/\partial {\varphi }_i\\ ⋮\end{array}\right]$$
初始化参数 ${\varphi }_i$ 是通过很多个${\theta }_i$来影向 $l(\hat{\theta }):$

根据链式法则：
$$\frac{\partial l(\hat{\theta })}{\partial {\varphi }_i}=\sum _j\frac{\partial l(\hat{\theta })}{\partial {\hat{\theta }}_j}\frac{\partial {\hat{\theta }}_j}{\partial {\varphi }_i}\text{\hspace{1em}(4)}$$
上式中 $\frac{\partial l(\hat{\theta })}{\partial {\hat{\theta }}_j}$ 很好计算, 根据损失函数的形式直接求即可，例如如果是交叉嫡，就用交叉嫡求偏导即可。重点来看后面这项: $\frac{\partial {\hat{\theta }}_j}{\partial {\varphi }_i}$

根据公式3可知, $\hat{\theta }$ 是一个向量, 所以我们可以找其中一个分量: ${\hat{\theta }}_j,$ 由公式3可得:
$${\hat{\theta }}_j={\varphi }_j-ϵ{\nabla }_{{\varphi }_j}l(\varphi )={\varphi }_j-ϵ\frac{\partial l(\varphi )}{\partial {\varphi }_j}\text{\hspace{1em}(5)}$$
对公式5中求 ${\varphi }_i$ 的偏导：

当 $i\ne j$ 时
$$\frac{\partial {\hat{\theta }}_j}{\partial {\varphi }_i}=-ϵ\frac{\partial l(\varphi )}{\partial {\varphi }_i\partial {\varphi }_j}$$
当 $i=j$ 时
$$\frac{\partial {\hat{\theta }}_j}{\partial {\varphi }_i}=1-ϵ\frac{\partial l(\varphi )}{\partial {\varphi }_i\partial {\varphi }_j}$$
算二次偏导很麻烦, 原论文提出忽略二次偏导项:

当 $i\ne j$ 时
$$\frac{\partial {\hat{\theta }}_j}{\partial {\varphi }_i}=-ϵ\frac{\partial l(\varphi )}{\partial {\varphi }_i\partial {\varphi }_j}\approx 0\text{\hspace{1em}(6)}$$
当 $i=j$ 时
$$\frac{\partial {\hat{\theta }}_j}{\partial {\varphi }_i}=1-ϵ\frac{\partial l(\varphi )}{\partial {\varphi }_i\partial {\varphi }_j}\approx 1\text{\hspace{1em}(7)}$$
把公式6和公式7代入公式4, 由于当 $i\ne j$ 时, $\frac{\partial {\hat{\theta }}_j}{\partial {\varphi }_i}=0,$ 所以求和的时候只用考虑 $i=j$ 的情况，即公式4可以写为:
$$\frac{\partial l(\hat{\theta })}{\partial {\varphi }_i}=\sum _j\frac{\partial l(\hat{\theta })}{\partial {\hat{\theta }}_j}\frac{\partial {\hat{\theta }}_j}{\partial {\varphi }_i}\approx \frac{\partial l(\hat{\theta })}{\partial {\hat{\theta }}_i}\text{\hspace{1em}(8)}$$
利用公式8的估计，梯度矩阵就变成了:
$${\nabla }_{\varphi }l(\hat{\theta })=\left[\begin{array}{c}\partial l(\hat{\theta })/\partial {\varphi }_1\\ \partial l(\hat{\theta })/\partial {\varphi }_2\\ ⋮\\ \partial l(\hat{\theta })/\partial {\varphi }_i\\ ⋮\end{array}\right]=\left[\begin{array}{c}\partial l(\hat{\theta })/\partial {\hat{\theta }}_1\\ \partial l(\hat{\theta })/\partial {\hat{\theta }}_2\\ ⋮\\ \partial l(\hat{\theta })/\partial {\hat{\theta }}_i\\ ⋮\end{array}\right]={\nabla }_{\hat{\theta }}l(\hat{\theta })$$
最后我们的梯度优化项就变成了：
$${\nabla }_{\varphi }L(\varphi )={\nabla }_{\varphi }\sum _{n=1}^N{l}^n\left({\hat{\theta }}^n\right)=\sum _{n=1}^N{\nabla }_{\varphi }{l}^n\left({\hat{\theta }}^n\right)=\sum _{n=1}^N{\nabla }_{{\hat{\theta }}^n}{l}^n\left({\hat{\theta }}^n\right)$$

真正的实现

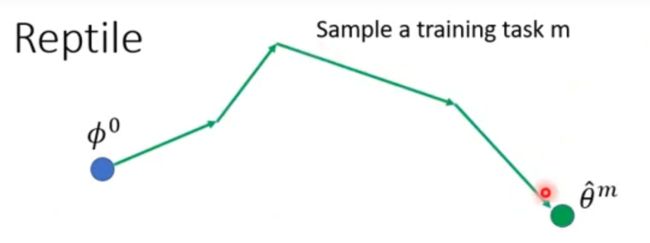
先要有一个初始化参数${\varphi }^0$，然后把一个任务task看做是一个sample，当然可以用多个任务组成mini-batch，然后做GD，这里不是batch，而是用SGD：

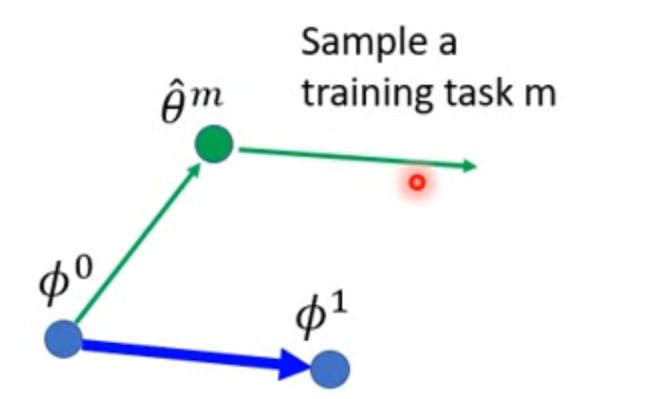
基于${\varphi }^0$计算网络在任务 m 上的损失函数，然后用SGD优化${\varphi }^0$，以学习率 $\epsilon $ 得到任务 m 独有的网络参数 ${\hat{\theta }}^m$；

虽然说好只更新一次，但是这里还是更新两次：

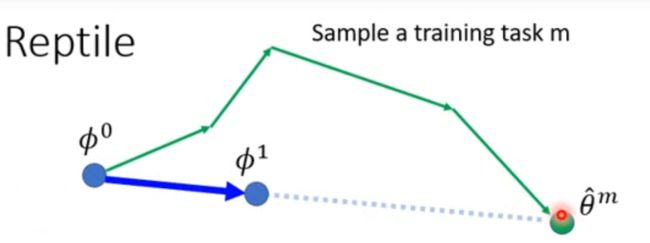
接下来，在第二个绿色箭头，基于${\hat{\theta }}^m$计算任务 m 新的损失函数，并求出损失函数在 ${\hat{\theta }}^m$上的梯度 ${\nabla }_{\varphi }{l}^m\left({\theta }^m\right)$ 。我们不是用这个梯度优化 ${\hat{\theta }}^m$，而是优化最初的那个${\varphi }^0$，即${\varphi }^1={\varphi }^0-\eta {\nabla }_{\varphi }{l}^m\left({\theta }^m\right)$。如第一个蓝色箭头所示，该箭头和第二个绿色箭头是平行的，代表${\varphi }^0$的更新方向为${\hat{\theta }}^m$处的梯度。

这里需要注意，同向的绿色和蓝色箭头不一定等长，因为LR可能不一样。

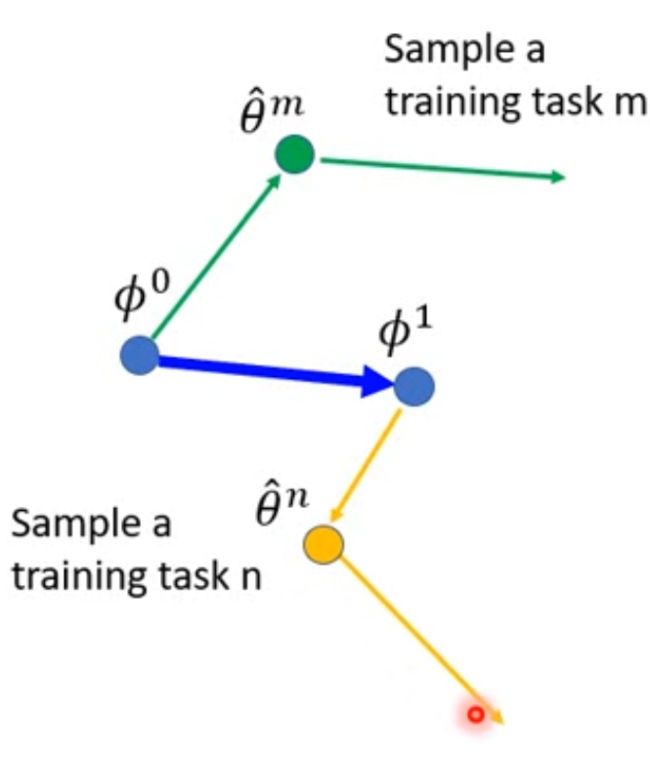
然后取一个任务n（Sample a training task n）同样用 ${\varphi }^1$ 计算出 ${\hat{\theta }}^n$ ， 以及 ${\hat{\theta }}^n$ 的下一次梯度方向

取其方向作为 ${\varphi }^1$的梯度更新方向：

这里需要注意，同向的黄色和蓝色箭头不一定等长，因为LR可能不一样。

再次对比transfer learning的Model Pre-training在实现上和MAML有什么不一样：

现有一个初始化参数：

然后计算 ${\hat{\theta }}^m$

然后沿着绿色箭头更新 ${\varphi }^0$

然后不断重复：

MAML 应用：Translation

Meta-Learning for Low-Resource Neural Machine Translation

18 training tasks: 18 different languages translating to English

2 validation tasks: 2 different languages translating to English

实验结果中用的是BLEU来做评估，横轴是数据量，当然数据量越大效果越好。Baseline是多任务学习。先看验证集结果，罗马语翻译为英文

测试任务结果，法语翻译英文

7、Reptile

On First-Order Meta-Learning Algorithms

Reptile算法流程

1. 首先初始化一个网络模型的所有参数 $\varphi$

2. 迭代 $\mathrm{N}$ 次, 进行训练, 每次迭代执行:

• $2.1$ 随机抽样一个任务 $t$, 用网络模型进行训练, 对应的loss 是 $L_t$, 训练结束后的参数是 $\tilde{\varphi }$
• $2.2$ 在参数 ${\varphi }_{}$ 上使用SGD 或 $Adam$ 执行$K$次梯度下降更新, 得到 $\tilde{\varphi }=U_t^k(\varphi )$
• $2.3$ 用 $\tilde{\varphi }$ 更新meta网络模型模型参数, $\varphi =\varphi +\eta (\tilde{\varphi }-\varphi )$

3. 完成上述$N$次迭代训练, 则结束整个过程

从上面的算法中可以看出, Reptile 是在每个单独的任务执行K次训练后, 就开始真正更新网络模型的参数 (Meta)，更新方式不是梯度下降, 但是和梯度下降公式长得很像, 是用上一次的参数 $\varphi$ 和K次后的参数 $\tilde{\varphi }$ 的差来更新, 更新的步长是 ${ϵ}_{\circ }$ 在这个过程中，只有一阶求导 的计算, 就是在任务内部$执行K$次更新的过程中用到的随机梯度下降, 这也是为什么标题中叫 First-Order 的原因。

从这就可以看出和 MAML 算法的不同了：

1. MAML：所有任务执行完, 用每个任务测试集上的平均 loss 来更新 meta 参数。
2. Reptile: 每个任务执行K次训练后, 用最新的参数和 meta 参数的差来更新 meta 参数。

这里说的meta参数, 就是真正更新网络模型参数的过程

梯度更新过程

$\varphi$ 代表网络模型初始参数, $\eta ，ϵ$ 分别代表 meta 更新的学习率和 task 更新的学习率, $N$ 是meta训练的 batch_size，即 meta 的一个bach有 $N$ 个task，每个task内部执行$K$次训练，$N$个任务都训练完，再来更新meta参数。按照上面的算法过程，meta的一个batch训练完之后，网络模型的参数是：
$$\begin{array}{rl}\varphi & =\varphi +\eta \frac{1}{N}\sum _{i=1}^N\left({\tilde{\varphi }}_i-\varphi \right)\\ & =\varphi +\eta (W-\varphi )\end{array}$$
其中 $W$ 是每个任务最后参数的平均值, 上述公式再进行展开就是这样
$$W=\frac{1}{N}\sum _i^{N}w=\frac{1}{N}\sum _i^N\left(\varphi -ϵ\sum _j^k{g}_{ij}\right)$$

$$\begin{array}{rl}\varphi & =\varphi +\eta (W-\varphi )\\ & =\varphi +\eta \left(-\frac{ϵ}{N}\sum _i^N\sum _j^k{g}_{ij}\right)\\ & =\varphi -\frac{ϵ\eta }{N}\left[\left(g_{11}+g_{12}+\cdots +g_{1k}\right)+\cdots +\left(g_{N1}+g_{N2}+\cdots +g_{Nk}\right)\right]\end{array}$$

假设$N=2,K=3$，即meta每次训练的一个batch 有2个task，每个task内部进行3此迭代，则 meta每次更新模型参数的公式为：
$$\begin{array}{rl}& \begin{array}{rl}N& =2,k=3\\ W& =\frac{1}{2}\left[\left(\varphi -ϵg_{11}-ϵg_{12}-ϵg_{13}\right)+\left(\varphi -ϵg_{21}-ϵg_{22}-ϵg_{23}\right)\right]\\ \varphi & =\varphi +\eta (W-\varphi )\\ & =\varphi -\frac{ϵ\eta }{2}\left[\left(g_{11}+g_{12}+g_{13}\right)+\left(g_{21}+g_{22}+g_{23}\right)\right]\\ & =\varphi -\beta \left(g_{11}+g_{12}+g_{13}\right)-\beta \left(g_{21}+g_{22}+g_{23}\right)\end{array}\end{array}$$

训练过程

meta 模型的参数更新过程，在几何上就是这样的：

动图看的更加清晰些，其中绿色代表第一个任务，三个绿色箭头代表三次更新时的梯度方向，可以看到，Reptile的模型就是朝着每个任务的梯度和的方向上不断地进行更新。

现有初始化参数 ${\varphi }^0$

取一个任务m（Sample a training task m）,Reptile没有规定只能更新一次参数，因此：

从 ${\varphi }^0$到 ${\hat{\theta }}^m$ 方向就是 ${\varphi }^0$ 更新的方向：

计算出 ${\varphi }^1$ 后，取一个任务n (Sample a training task $\mathrm{n}$ ) 同样用 ${\varphi }^1$ 计算出 ${\hat{\theta }}^n$ 并更新多次，取 ${\varphi }^1$ 到 ${\hat{\theta }}^n$ 的方向作为 ${\varphi }^1$ 的更新方向：

把pre-train, MAML, Reptile都放在一起看下有什么区别:

下面 $g_1$ 是pre-train的更新方向 ,$g_2$ 是MAML的更新方向, $g_1+g_2$ 是Reptile的更新方向, 当然还可以更新更多次.

8、More about Meta Learning

上面讲的MAML和Reptile都是关于用Meta Learning来找初始化参数这个事情，那我们在介绍Meta Learning的时候还有很多红色框框，这些也是可以用Meta Learning来进行研究如何学习的。

下图是用network来设计Architecture & Activation，以及如何更新参数。

我们之前讲的都是用这种方法来更新我们的初始化参数，那么能不能有别的应用呢！其实是可以的，我们可以更新我们的神经网络的结构，也可以更新他们的更新的方法。当让我们用一个网络去更新另一个网络的话，我们是没有办法进行微分的，所以我们经常使用rl的方法进行更新。

其实我们之前是训练如何设置初始化参数${\varphi }^{}$ ，但是我们本身就有一个初始化参数${\varphi }^0$ 。

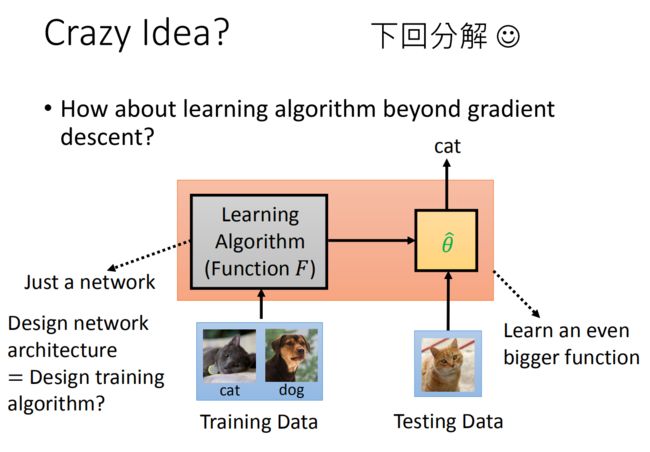
于是我们就有了一个十分疯狂的想法，就是我们让我们的learning algorithm本身就是一个大的network，之后我们去让神经网络输出我们训练的参数θ，之后我们再用参数θ的分类网络去分类，得到我们最终的预测标签。那么我们可不可以把learning algorithm网络和分类网络两个网络都搞在一起呢！就是我们直接将两个网络都设置为黑盒，输入的是training data，之后再黑盒里得到我们的参数和模型，我们不知道参数是什么，不知道模型是什么，我们就可以直接得到我们的分类结果了。

这就是 8.9 元学习网络结构讲解 的内容了。

参考资料

李宏毅2020人类语言处理

课程向：深度学习与人类语言处理

计算机视觉实验室

人工不智能，机器不学习

[meta-learning] 对MAML的深度解析

https://openai.com/blog/reptile/