数据结构 二叉树的顺序结构原来要这么写

       二叉树的顺序结构有一个专属的名称 堆, "堆" 我熟,他不就是动态开辟的数据都存在那里吗,他业务那么广阔还可以用到树里,其实他们不是同一种东西,同名罢了

---

堆的一些概念

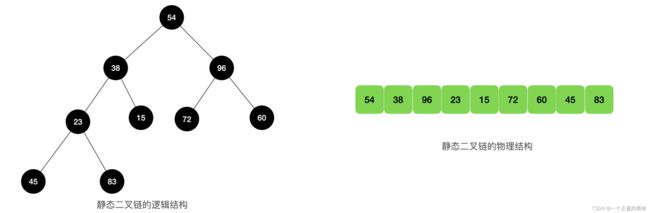
看看数据结构里面的堆是啥：可以堆理解逻辑结构像是堆上去的，类似金字塔❕❕❕树不是也这样吗,当然堆其实也是二叉树，但他是二叉树的一种变形: 完全二叉树，是基于顺序表结构存储

如图：

      如上图那样存储如何找他的子节点呢？父节点也没存他的子节点的指针,那要如何访问呢？发明出来总是拿来用的,那么来看看大佬是如何想出来的(他有一点 静态链表 的感觉 ）

静态链表简单描述

• 用数组实现链表,定义结构的时候留一个数据存他后面插入的下标,可是他还有空间浪费,不想指针练表那么灵活

如何找自己的子节点呢？其中有俩条重要的定义：

公式1: 左孩子=父节点*2+1
公式2: 父节点= (孩子-1)/2

      有了这俩个公式之前的疑惑也就烟消云散了,既然可以找到子节点,还可以找到父节点,那么好办事了,那么就介绍一个比较厉害的东西,堆排

---

堆排

     他是基础排序中其中之一,是一位优秀的选手,时间复杂度是N*log^N (后文推导), 相比冒泡排序(n²)已经是快的没边了,废话不多说,正式介绍一下堆排

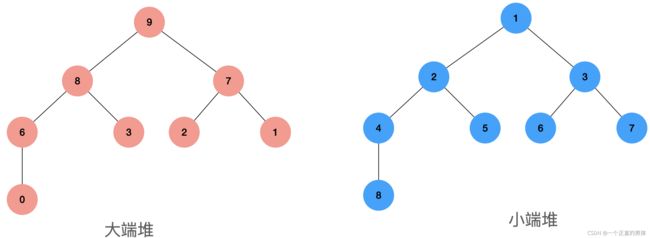
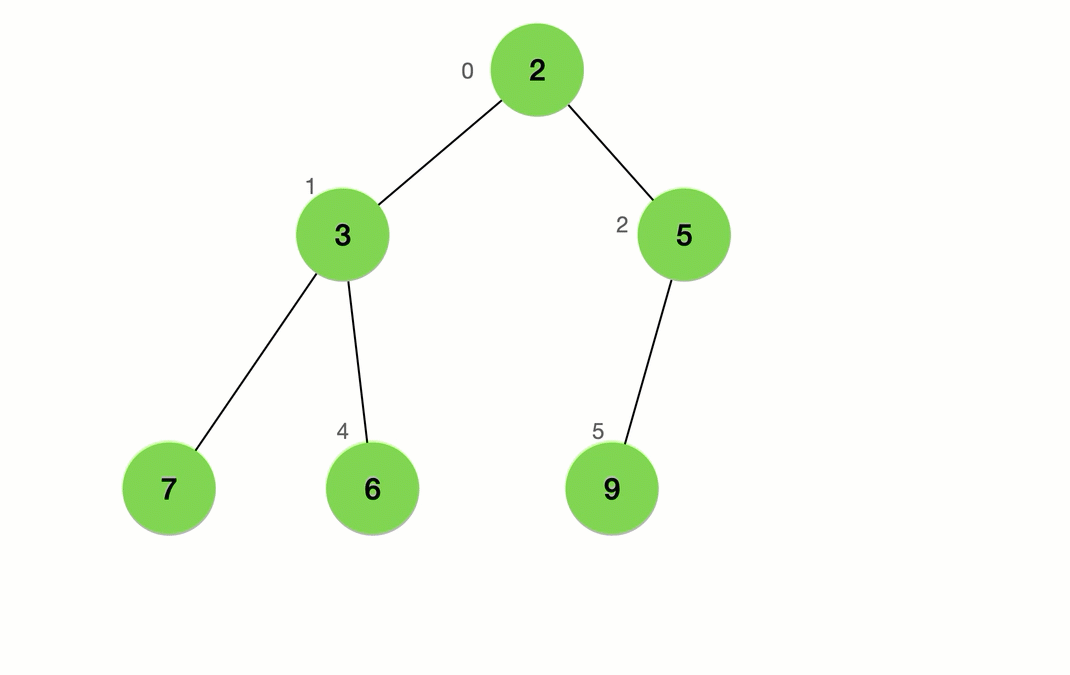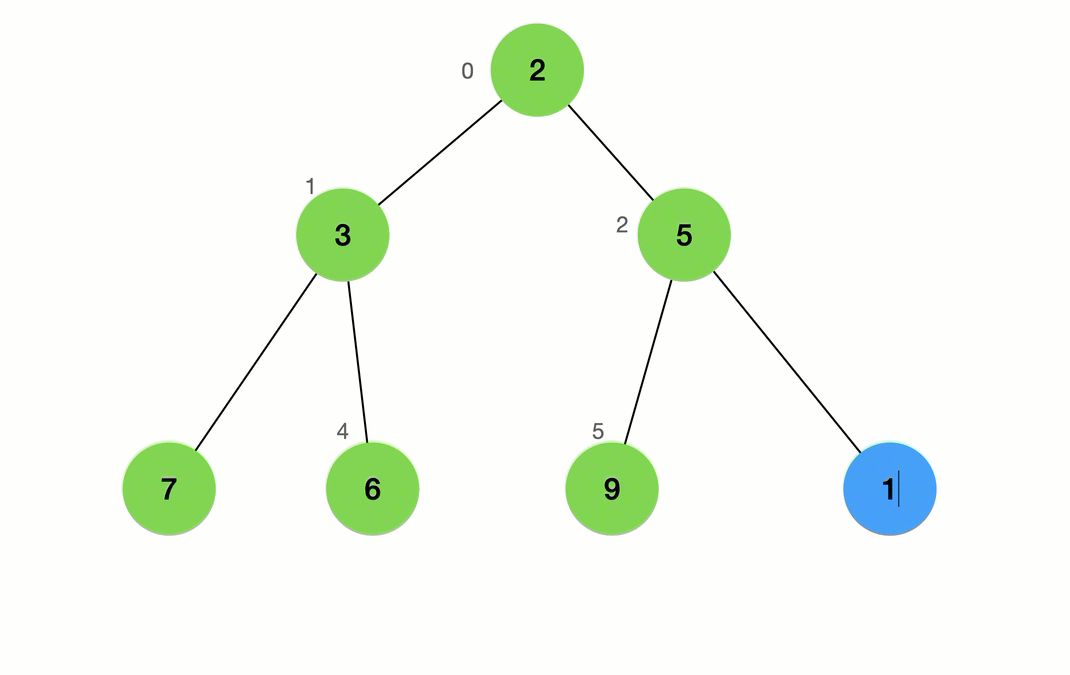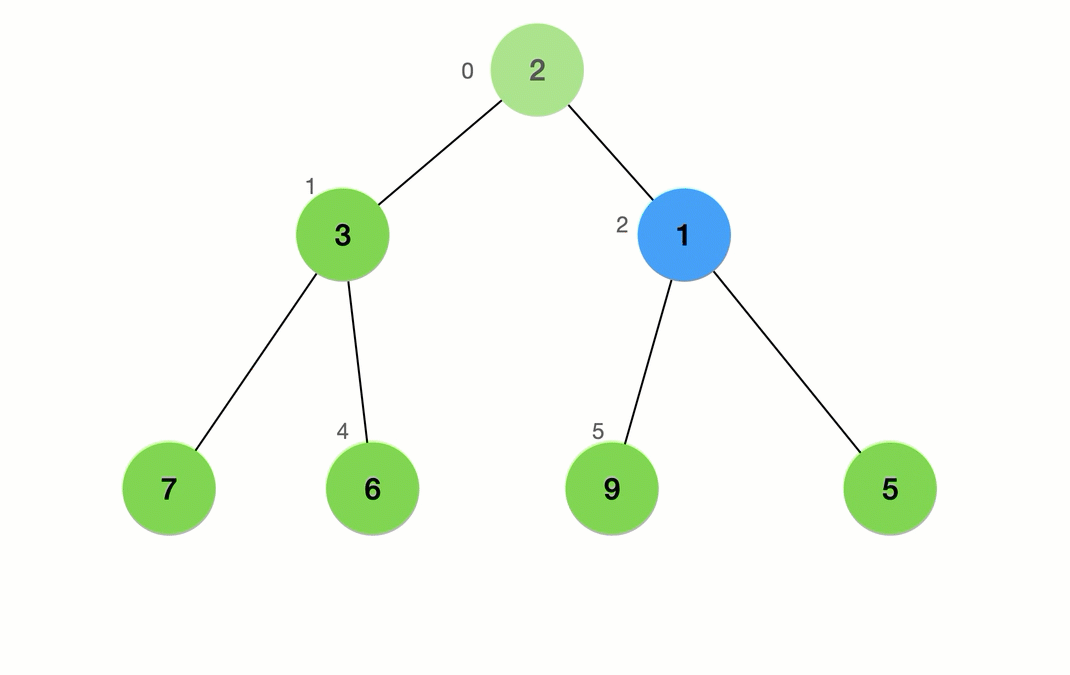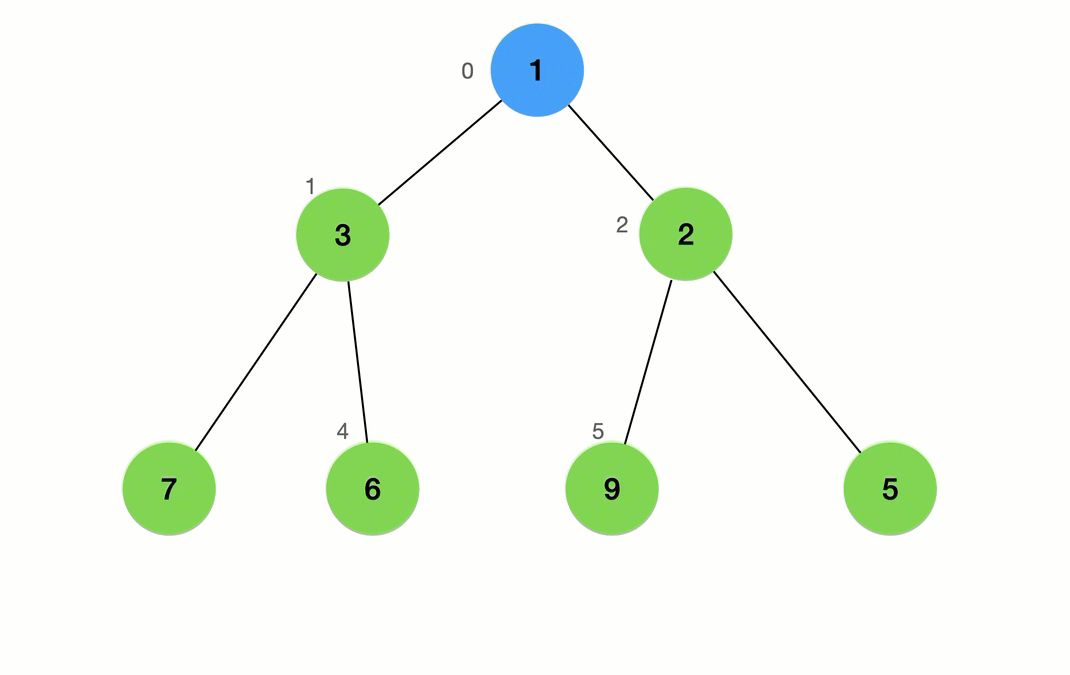
     堆分为俩在结构 , 大端堆 , 与小端堆 , 这是俩是啥 , 人如其名,大端堆所以的父节点一定比孩子大，小端反之
如图：

       这个时候可能有入要说了，我的完全二叉树这么不是这样的，数据都是大小不一的，你这个不会就是自己现象出来的逻辑结构吧，其实不是要变成上图那个模样，需要进行俩个操作建堆            排序

---

建堆

       建堆可谓是堆排中最重要的一步，没有他别的都是后话，因为堆排是在大端堆或者小端堆的基础进行，如上文所说，一棵树一般情况下不太会是就是大端 or 小端，甚至不太会是一棵完全二叉树可他是如何建堆的呢？

       下文呢能会觉得有点巧，其实这些都是计算机的先辈研究出来的就像之前的那个三步翻转法，希尔算法(之后的博客会介绍)

建立基于上文的俩个公式:
思路：

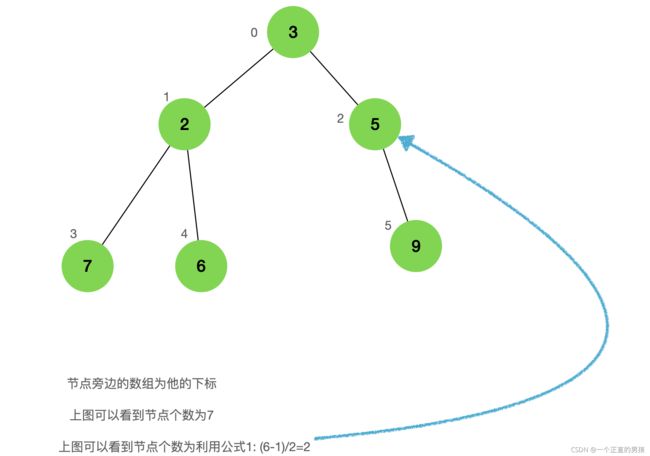
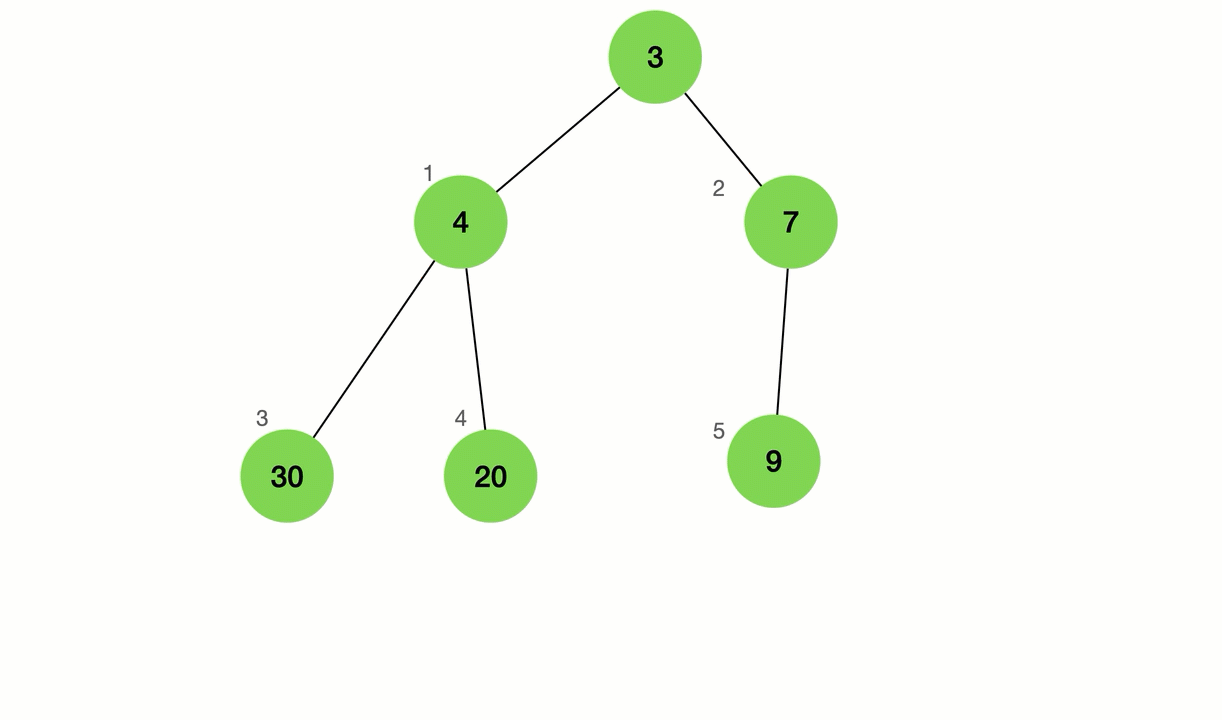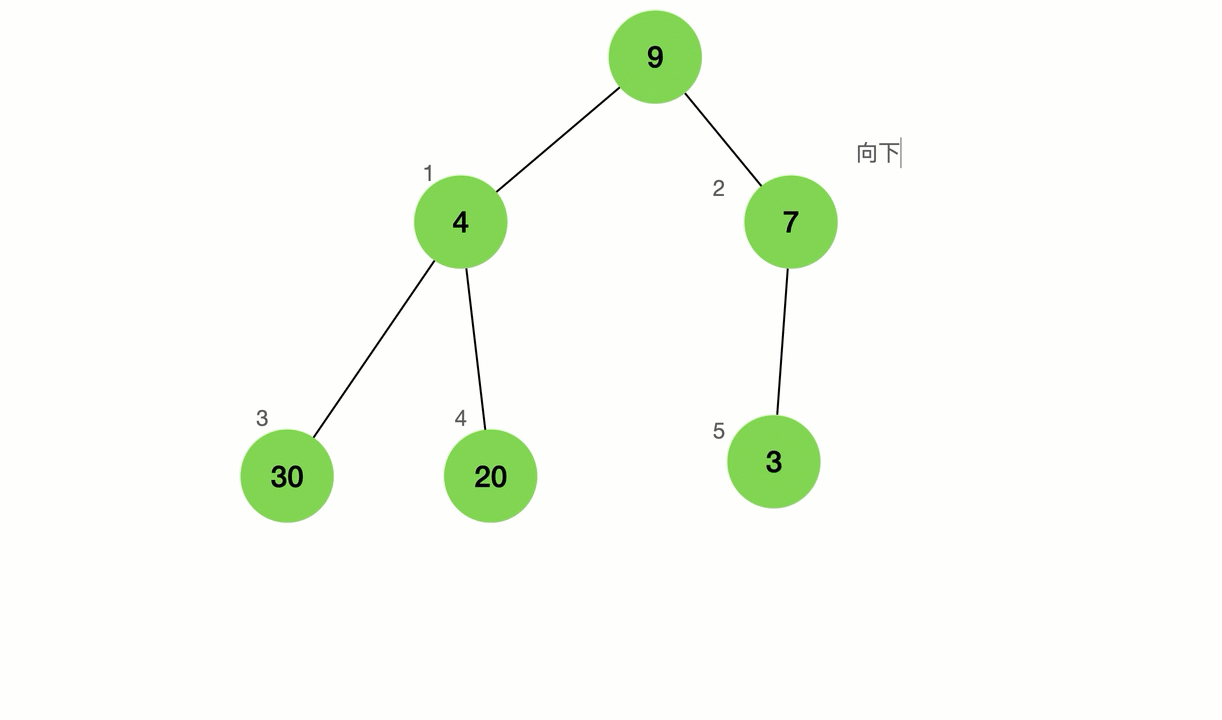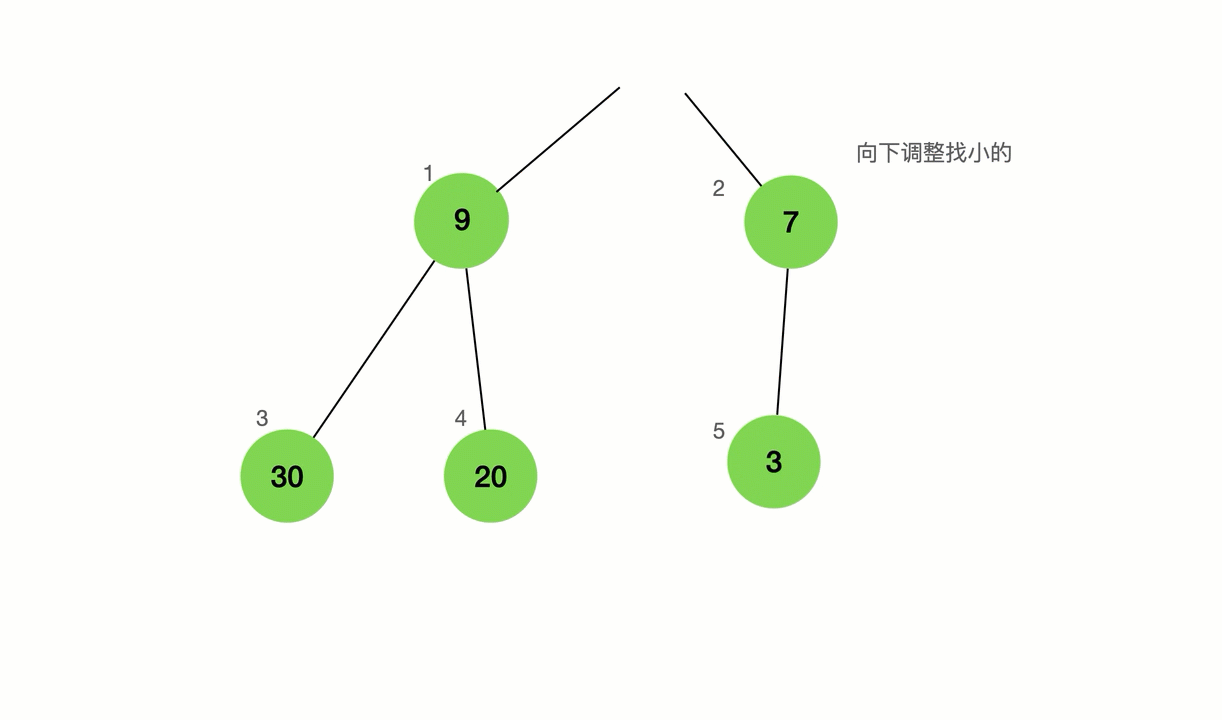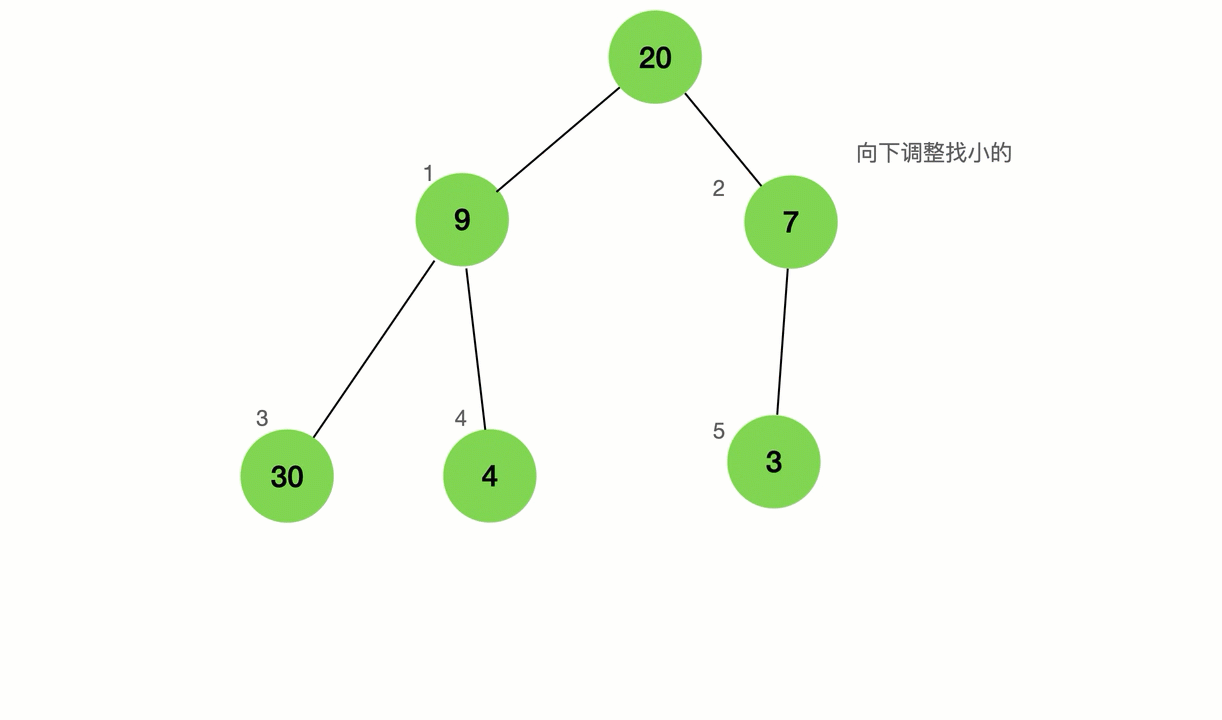
通过公式1+节点个数，我们就可以找到最后一个带有叶子的节点

如图

       在比较他子节点的个数是不是小于他或者大于他如果大于就交换，且和孙子节点比直到父亲节点小，比子节点大,这个过程有一个专属的名词向下调

向下调整

       如果说建堆是堆排的核心，那么向下调整就是就是建堆的核心

代码

void AdJustDown(int* a, int n, int root)//向下调整
{
     
    int parent=root;//父亲节点
    int child=parent*2+1;//左孩子节点
    while(child<n)//如果孩子节点大于节点个数比下去就越界了
    {
     
        if(child+1<n&&a[child]<a[child+1])//如果右孩子大于左孩子判断为真
        {
     
            child=child+1;//如果右孩子大就吧左孩子置为右孩子节点
        }
        if(a[parent]<a[child])//如果孩子大于父亲判断为真
        {
     
            Swap(&a[parent],&a[child]);//交换
        }
        
        //更新父亲，孩子节点
        parent=child;
        child=parent*2+1;
    }
}

建堆代码

   int parent=(n-2)/2;//最后一节点的父亲
    for(int i= parent;i>=0;i--)//这个就是上文说的巧的代码，每进一次循环都会让这个节点变得有序
    {
     
        AdJustDown(a,n,i);
    }

运行动图

请配合上面的代码食用

排序

       排序那么如何排序那？排升序是要 建大堆呢？还是建小堆？那么先看一下如何排序吧，看完就豁然开朗了

排序思想：

尾巴元素和首元素交换在向下调整

代码：

   int end=n-1;//最后一个节点
    for(int i =end;i>=0;i--)//控制end，每次迭代end
    {
     
        Swap(&a[0],&a[i]);//首元素和尾元素交换
        AdJustDown(a,i,0);//向下调整
    }

运行动图

       上面这个动图其实就可以看出排升序要建大堆，为啥呢，那么看建小堆如何走的
动图演示：

显然可以看出，建立小堆排的话就是降序

结论：
排升序建大端，排降序建小端

拓展

       堆其实是一个数组，那么他可以和顺序表一样尾插数据吗？当然可也，那么他如何保持有序呢？？？

向上调整
思想：

       在有序的情况下 , 找到父节点和父节点比较如果比父节小 ( 升序的情况 )交换，这是向下调整逆推的一个过程

如图：

       在这个过程中有人看能要问了，他和父节点交换如果左孩子比他小这么办(升序), 那不会，你想是在有序的情况下，那么父节点一定是比他的孩子要的大

代码：

void AdjustUp(int *arr,int tmp,int son)//调整
{
     
    int father= (son-2)/2;
    while(son>0)
    {
     
        if(arr[father]>arr[son])
        {
     
            Swap(&arr[father],&arr[son]);
            son=father;
            father=(son-1)/2;
        }
        else
        {
     
            break;
        }
    }
}

向上调整建堆

       既然向下调整可以建堆，那么向上调整可以建吗？他有点类似尾插

思路：

从头开始一次拿一个，每次插入都向上调整

图解：

时间复杂度

上文说堆的时间复杂度是O(Nlog₂N)，如何算呢

推导：
       上文可以看到在排序的时候的是要走N次的，且每次都要向下调整，向下调整如何计算呢，一般算的是最坏的情况，那么就是每一层都要比，那么如何算层数呢，log(节点个数)，因此推导出来是O(Nlog(N))